《电磁散射理论与工程》作业
1.请参考课本中线性调频连续波体制下对目标成像相关内容,论述三维成像机理并讨论成像分辨率影响因素
线性调频连续波(FMCW)雷达在三维成像中,通常利用距离、方位角和俯仰角三个维度的信息来生成目标的三维图像。[1]
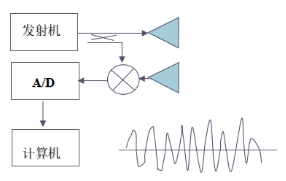
图 1 FMCW系统框图
以下是FMCW雷达实现三维成像的详细机理:
\距离测量原理:**
FMCW雷达利用发射信号与回波信号的频率差来测量目标距离,其中发射信号为频率线性调制的连续波信号,回波信号为目标反射回来的信号。
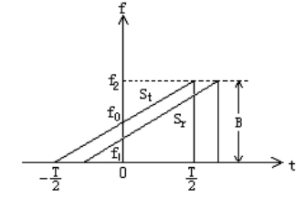
图 2 发射和接收信号波形图
FMCW雷达发射的信号频率随着时间线性变化,可以表示为
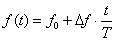
其中,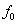 是起始频率,
是起始频率,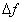 是频率偏移量,
是频率偏移量,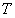 是调制周期。发射信号可表示为
是调制周期。发射信号可表示为
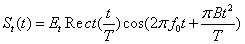
回波信号是目标反射回来的信号,经过时间延迟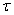 后,其可以写为
后,其可以写为
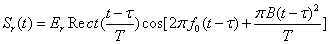
频率变为
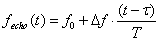
其中, 为发射信号的频率随时间变化的曲线,
为发射信号的频率随时间变化的曲线, 为理想点目标散射后被接收信号的相应曲线。扫频信号的起始频率为
为理想点目标散射后被接收信号的相应曲线。扫频信号的起始频率为 ,终止频率为
,终止频率为 ,扫频带宽为
,扫频带宽为 ,扫频周期为
,扫频周期为 。
。
通过混频处理得到的频率差 为
为
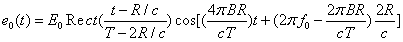
其频率为
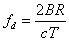
相位为
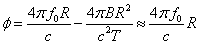
距离信息包含在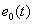 中,故通过FFT,就可以得到目标在距离上的分布。[2]
中,故通过FFT,就可以得到目标在距离上的分布。[2]
\角度测量原理:**
FMCW雷达通过天线阵列测量目标的方位角和俯仰角,通常采用相控阵或干涉技术来实现,相控阵天线通过调整各个阵元的相位,实现波束的电子扫描,从而确定目标的方位角和俯仰角。
多个天线接收同一目标的信号,计算其相位差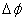 与目标的角度
与目标的角度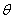 的关系为
的关系为
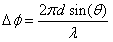
其中,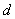 是天线间距,
是天线间距,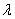 是信号波长。
是信号波长。
\三维成像处理******[3]****:****
雷达成像技术的研究内容是获取更为丰富的目标特征信息,经过将近60多年的发展,雷达成像技术的观测对象已从最开始的点目标发展成如今的在复杂背景中具有一定位置、姿态和运动参数的扩展目标。其中取代实孔径的合成孔径(SAR,ISAR)技术、宽频带技术对接收到的信号进行傅里叶变换,分别提高了成像的横向和纵向分辨能力,进而获得目标的距离和角度信息,综合距离信息和角度信息,通过数字信号处理技术生成目标的三维图像。
从系统的观点来分析上文的处理过程,通过对标校点散射源的测试以期获得成像系统的系统函数(系统点源散射响应函数),从目标的回波数据中剔除该系统特征(天线方向特性,背景杂波空间频率响应,收发系统的频率响应)完成匹配滤波,进而提取目标特征像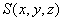 。
。
图 3 微波三维成像数据处理流程图
步进扫频雷达天线测试系统,在位置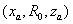 上综合形成一矩形口径区域,以连续波的形式波数
上综合形成一矩形口径区域,以连续波的形式波数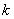 为对目标进行探测,目标回波数据
为对目标进行探测,目标回波数据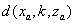 。
。
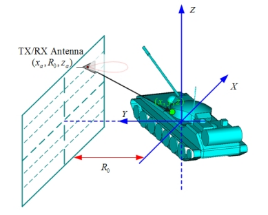
图 4 微波三维成像测试示意图
假设目标由若干散射中心构成,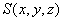 是目标雷达反射率的空间分布。
是目标雷达反射率的空间分布。
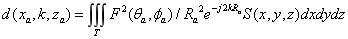
其中波程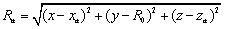 ,
,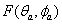 于
于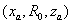 上天线在
上天线在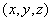 上的方向特性图,天线指向角
上的方向特性图,天线指向角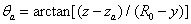 ,
,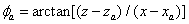 ,对各频点上的数据沿扫描方向上做傅立叶变换,
,对各频点上的数据沿扫描方向上做傅立叶变换,
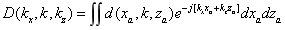
当目标为金属球点散射源时,其像函数为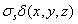 ,其回波数据经如上处理可得
,其回波数据经如上处理可得
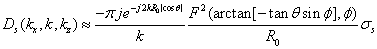
两式相除,并乘以金属球像函数幅度可得
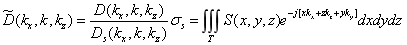
将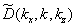 插值实现均匀采样
插值实现均匀采样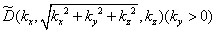 后,做傅立叶逆变换获得目标的像
后,做傅立叶逆变换获得目标的像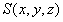 。
。
\影响成像分辨率的因素:**
a) \带宽:**线性调频连续波雷达的距离分辨率与发射信号的带宽成反比,带宽越大,距离分辨率越高。距离分辨率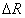 可以表示为
可以表示为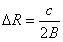 因此,增大发射信号的带宽
因此,增大发射信号的带宽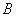 可以提高距离分辨率。
可以提高距离分辨率。
b) \天线阵列的尺寸:**较大的天线阵列和适当的阵列设计可以提高方位角和俯仰角的分辨率。角度分辨率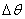 与天线阵列的孔径
与天线阵列的孔径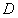 的关系为
的关系为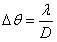 ,阵列尺寸越大,角度分辨率越高。
,阵列尺寸越大,角度分辨率越高。
c) \信号处理算法:**先进的信号处理算法可以显著提高成像分辨率和质量。例如压缩感知技术通过稀疏信号重构技术,可以在采样率低于奈奎斯特采样率的情况下,实现高分辨率成像;MUSIC算法和ESPRIT算法,可以突破传统的雷达分辨率极限,实现超分辨率成像。
d) \噪声和干扰:**环境噪声和电磁干扰会影响成像质量和分辨率,采用适当的滤波和去噪算法可以减小这些影响。卡尔曼滤波和维纳滤波可以有效地抑制噪声;小波变换去噪和自适应去噪算法可以在保留信号特征的同时去除噪声。
e) \系统稳定性:**系统的稳定性如天线阵列的相位和幅度校准、信号路径校准和校准精度等对成像分辨率有重要影响,高精度的系统校准和稳定的硬件设计可以保证成像结果的准确性和可靠性。
综上所述,FMCW雷达在三维成像中的应用涉及距离测量、角度测量和成像处理等多个方面。带宽、天线阵列尺寸和排列、信号处理算法、噪声和干扰以及系统稳定性和校准精度等因素都会影响成像分辨率,通过优化这些因素,可以获得高质量的三维成像结果。
2.请结合课程内容查阅一篇近期有关电磁散射计算的论文,作总结与评述;
我阅读的文献是由**南京理工大学**电子工程与光电技术学院的**赵敏等**人在**2024年1月9日**发表在**《电波科学学报》**的**《不确定参数目标电磁散射特性计算及评估》******[4]****,本论文主要研究了在目标信息不完备和目标几何外形、材料属性等存在不确定性的情况下,电磁散射特性的计算方法和评估技术。
\总结:**
首先,作者介绍了基于泰勒级数展开的分析方法,利用NURBS技术对目标外形进行建模,并建立外形和介质参数与电磁积分方程之间的函数关系,从而分析目标电磁散射特性。其中不确定性的目标参数可以是外形、介电常数。
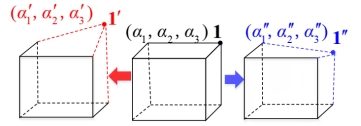
图 5 具有外形不确定的立方体模型
论文还提出了一种基于渐进波形估计(AWE)技术的高维不确定性目标电磁散射特性分析方法。该方法利用伪谱法求解各阶导数,相较于传统的公式求导方法能够节省大量的推导和计算时间;并且利用Padé近似方法计算目标改变后的最终电流,相较于泰勒级数展开方法能够准确计算更大的随机扰动量。与蒙特卡洛(Monte Carlo,MC)方法相比,AWE方法提高了计算效率,且仿真与实测结果吻合一致,尤其适用于高维不确定性问题。
为了进一步提高计算效率和准确性,论文还结合了BP神经网络,实现了对不确定性目标散射特性的置信度和不确定度的智能化计算,使用样本的RMSE决定对应角度所占的比重,这一方法不仅能够准确有效地分析非合作目标的高维不确定性问题,而且显著提高了计算效率。
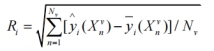
\评述:**
论文通过实际测量数据验证了所提方法的有效性,并展示了该方法在实际应用中的潜力,特别是在处理目标参数不确定性方面提出了有效的解决方案。基于泰勒级数展开的方法为不确定性分析提供了一种理论基础,AWE技术在此基础之上显著提高了计算效率,这对于大规模或实时散射特性分析尤为重要。BP神经网络的引入,不仅提高了评估的智能化水平,也为快速准确的置信度和不确定度评估提供了新的途径。实验验证中论文提及方法的结果与实测数据有较高的吻合度,证明了其在实际应用中的可靠性。但是,该方法在计算方法的进一步优化、算法的普适性以及更广泛应用场景的适应性方面仍有提升空间。
3.请结合课程内容查阅一篇近期有关电磁散射测量的论文,做总结与评述
我阅读的文献是由**西安电子科技大学**的**王闻岩等**人在**2023年5月14日**发表在中国山东青岛的**《2023年全国微波毫米波会议》**中发表的**《外场条带式散射成像系统研究》******[5]****,这篇论文通过设计一种外场滑轨测试架,构造多功能、标准化、模块化的测试平台。通过改变电磁算法就可以在该平台上进行多种电磁测量工作,可以针对不同的测试方案精确控制仪器设备的方位和速度信息,提高外场实验的质量和效率,优化采集的数据,在外场复杂的环境下建立能够精准控制实验流程的系统。
\总结:**
本文提出了一种外场条带式散射成像系统,该系统针对电磁散射测量领域,特别是在地面环境的电磁散射特性研究中具有重要意义。通过设计外场滑轨测试架,实现了一个多功能、标准化、模块化的测试平台,能够根据不同的测试需求,改变电磁算法来执行多种电磁测量任务。
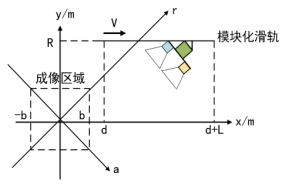
图 6 模块化外场滑轨地物SAR图像测量简化图
这一设计显著提高了外场实验的质量和效率,优化了数据采集过程,并在复杂环境下实现了对实验流程的精准控制。此外,论文还详细阐述了合成孔径雷达(SAR)成像的基本原理,包括信号模型、变标操作和多普勒域信号处理等关键技术,为电磁散射测量提供了理论基础和技术支持。
在测量速度的确定上,论文依据奈奎斯特采样定理,提出了一种计算合适滑轨运动速度的方法,以确保在雷达参数一定的情况下,既不会造成测量时间的浪费,也不会因采样点过少而导致SAR图像模糊,影响图像分辨率。此外,论文还详细介绍了测量平台的硬件设计,包括频谱仪的使用、信号放大器的配置以及天线的选择等,这些都是为了确保信号的有效发射与接收,降低信号损失率,提高测量的准确性。
图 7 地物电磁散射软件设计流程图
\评述:**
论文中提出的外场滑轨测试架设计,体现了高度的创新性和实用性,它不仅能够适应多样化的测量需求,而且通过模块化设计,提高了系统的灵活性和可扩展性,这种设计思路对于未来电磁散射测量技术的发展具有重要的启示作用。
但在实际应用中可能会遇到一些挑战,例如系统在不同环境条件下的适应性、成本控制以及长期运行的稳定性;论文中的算法和模型虽然在理论上是可行的,但实际测量中的噪声、误差以及环境因素可能会对测量结果产生影响;论文中对软件设计的描述,包括与矢量网络分析仪的通信、测量模式的设置以及IFFT处理等,为实际操作提供了清晰的指导,软件的易用性、用户界面的设计以及错误处理机制等方面也需要在实际应用中不断优化和改进。
4.综述基于无相近场幅度测量的相位反演方法;
天线测量是天线设计、研制、生产过程中重要的环节,是获得天线电参数、检验天线性能指标的重要手段。随着电磁理论研究的深入、微波技术的进步,天线设计朝着高频化、集成化发展,也对天线测量技术提出新的要求随着天线工作频率的上升,相位的测量精度受探头位置、运动误差和环境温湿度等因素的影响较大,存在无法精确获得待测天线的相位信息的问题。相位测量相比幅度测量需要更加复杂和昂贵的测试仪器,增加了天线测量的成本。随着无线电设备体化程度的提升,待测设备与测试仪器间无法建立物理连接,导致了相位无法获取的问题。
针对上述问题,国内外学者提出无相位天线测量技术,间接获取待测天线的相位。无相位测量技术可分为干涉测量法和迭代法——干涉测量法主要应用在光学领域,根据电磁波传播方程,通过引入参考光,待测光的相位信息可以编码在可测量的干涉光强分布中,离轴全息术利用参考光中的载波产生可检测的干涉条纹,在频域分离物波前、孪生像和零级像,从而实现波前重构;迭代法因其设置简单已成为目前的研究热点与重点,迭代法通常需要测量多个近场的幅度数据,通过相位恢复算法迭代还原出相位信息,但是迭代法需要更高的时间成本,且相位恢复算法存在陷于局部解的风险,恢复算法的收敛性受采样面选择和算法初始值的影响。
经典的相位反演算法包括Gerchberg-Saxton算法、错误减少算法(ER)、混合输入输出法(HIO)、梯度搜索算法几何光学的蒙日-安培方程方法、物理光学的迭代角谱算法等,这些算法利用迭代优化的方法,从初始猜测出发,通过不断调整相位信息,使得重建的幅度信息与实际测量值尽可能匹配。接下来,对几种常用的相位反演算法进行整理:
\Gerchberg-Saxton算法******[6]****:****基于迭代运算的相位复原法是于1972年,Gerchberg和Saxton在研究电子显微成像的相位恢复问题首次提出的,该算法称为Gerchberg-Saxton(GS)算法,当待测光波场在像平面(Imaging plane)和远场衍射平面(Diffraction plane)的光强分布已知时,光场波前相位可以通过衍射计算迭代的方式求解出来。
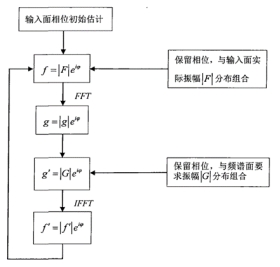
图 8 GS算法流程图
随机设置一个输入面上的初始相位,记为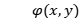 ,每次迭代开始时,都使用计算得到的
,每次迭代开始时,都使用计算得到的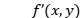 相位所替代,与己知输入平面上测量的光波振幅分布结合,构成入射光波函数
相位所替代,与己知输入平面上测量的光波振幅分布结合,构成入射光波函数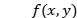 ;进行傅里叶变换得到其输出平面上的光波函数;取光波函数的相位,与输出面上测量得到的振幅分布结合,做傅里叶逆变换得到下一步迭代波函数
;进行傅里叶变换得到其输出平面上的光波函数;取光波函数的相位,与输出面上测量得到的振幅分布结合,做傅里叶逆变换得到下一步迭代波函数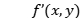 ;将以上步骤重复执行,一直到均方误差和SSE(Sum-Squre Error)小于规定的指标。
;将以上步骤重复执行,一直到均方误差和SSE(Sum-Squre Error)小于规定的指标。
\迭代角谱算法******[7]****:****角谱迭代算法基本思想是用随机相位作为迭代初始相位,利用平面角谱传播原理,在物面和像面之间反复迭代,从而获得物面相位信息。
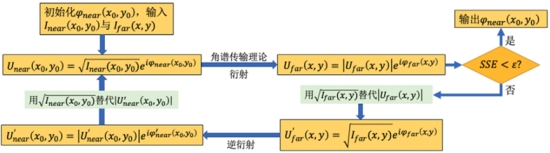
图 9 角谱迭代算法流程图
角谱迭代算法步骤主要包括:以随机相位作为物平面光波的初始相位分布,与己知的物平面光波振幅分布结合,得到初始的波前函数;再利用前向的角谱传播,就可以得到像平面上的波前函数;保留相位,把振幅替换成为通过测量得到的像平面上的光波振幅分布;得到的新的像面波函数,利用后向角谱传播得到物面上的波前函数;保留相位不变,将振幅变换为原先已知的物面的振幅分布,作为下一次迭代循环的初始物波函数;通过重复迭代计算操作,直到定义的均方误差和达到设定的精度或者达到设定的最大迭代次数。
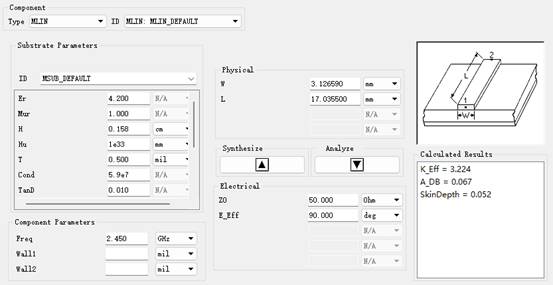
\基于非凸优化方法的无相位天线平面近场测量方法******[8]****:该方法基于源重构法,建立天线口径面上等效磁流与测量面电场间的联系,使用非凸代化还原口径面上的等效磁流的幅相信息,最后通过电场积分方程,计算出待测天线的远场方向图。相位还原问题可归纳为:
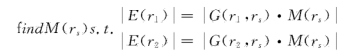
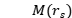 为通过凸优化算法还原得到的口径面等效磁流幅相信息,G为自由空间格林函数,是大小为
为通过凸优化算法还原得到的口径面等效磁流幅相信息,G为自由空间格林函数,是大小为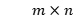 的复矩阵,也被称为测量矩阵。
的复矩阵,也被称为测量矩阵。
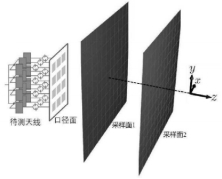
图 10 无相近场测量示意图
当相位信息不可获取时,源重构方法由求解线性方程组转变为非线性逆问题,通过引入RWF这一非凸优化模型,以恢复口径面上等效磁流源幅相信息。该算法以最小化代价函数为目标,通过梯度迭代搜索全局最小值,具有鲁棒性高,迭代速率较快,在低过采样率时也具有较高恢复性能的优点。为避免陷人局部收敛或鞍点,RWF引入自适应权重系数。若当前估计远离最优时,自适应权重系数将间接产生截断效应,使得算法能够以指数形式收敛至最优解。代价函数的全局最小值由梯度下降算法求解,沿梯度下降方向迭代搜索,直到全局最优值,获得口径面上等效磁流的幅相数据。最后,由电场积分方程即可获得待测天线远场方向图。
基于无相近场幅度测量的相位反演方法在现代电磁波成像和测量技术中具有重要地位,其不断发展的算法和应用拓展将为科学研究和工程应用提供更强大的工具。
5. 详述基于衍射神经网络的相位反演算法;
随着信息技术的发展,优化算法和深度学习等技术得到长足进步,大大增强了计算机系统对图像的恢复和解调能力。电磁场的传播可用复振幅来表述,其中包含电场的振幅和相位两种关键信息。电场场强仅与振幅相关,可直接由探测器测量,而相位则无法被电场学传感器直接检测。复振幅的相位信息携带了电场在介质中传播的重要信息,如厚度、折射率变化等,对智能检测和感知技术的发展有着重要的意义。波前重构技术可提取相位信息,实现从电场场强到复振幅的重构,从而显著提升电场学系统的成像质量和信息量,有助于提高系统的感知、分析和控制水平。
在成像领域的逆问题解决方案中,深度神经网络(DNN)的应用已逐渐成为焦点。DNN是一种拥有众多隐藏层的人工神经网络,其概念最初由McCulloch和Pittsu提出,在仿生学的基础上,通过模拟单一神经元的最基本计算单元,并通过计算单元间的互相连接来模拟神经细胞间的电信号传递。在20世纪90年代,人工神经网络在MNIST数据集上实现了超过98%的分类精度。在此基础上,LeCun等人[9]在2015年提出了深度学习的概念,强调多层神经网络可以从大量数据中学习到深层次的图像关联信息。近年来,得益于图形处理单元(GPU)计算能力的显著提升和特殊网络结构的设计,研究者能够训练和收敛更深层次的大型神经网络,如VGG、ResNet、GAN和Transformers,以实现更为复杂的图像处理任务。深度神经网络在多种计算机视觉任务中都取得了出色的表现,例如图像分类[10]、图像超分辨[11]、图像去噪[12]和图像生成[13]等,在自动驾驶、监控安防和生物显微成像等领域都得到了广泛应用。
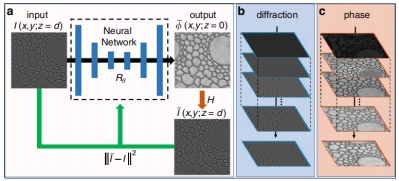
图 11 基于衍射神经网络的相位反演流程图[14]
基于衍射神经网络的相位反演算法可以不需要事先训练就使用,从而消除了成千上万标记的数据。通过神经网络与物理模型的相互作用,可以自动优化网络,最终产生对象阶段。物理网络不需要的真实数据,它使用一个物理模型 来计算衍射图样,使用惠更斯-菲涅耳原理计算出的
来计算衍射图样,使用惠更斯-菲涅耳原理计算出的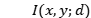 和测量的
和测量的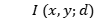 之间的误差,通过梯度下降来优化权重和偏差。随着迭代过程的进行,使计算出的衍射模式
之间的误差,通过梯度下降来优化权重和偏差。随着迭代过程的进行,使计算出的衍射模式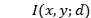 收敛到测量到的模式
收敛到测量到的模式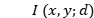 。
。
一个相干平面波照亮,其后面的复振幅可以写成
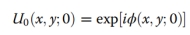
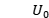 在传播距离
在传播距离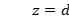 上的衍射值为
上的衍射值为
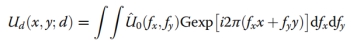
其中传递函数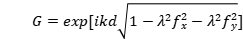 ,
, 是
是 的傅里叶变换,因此,由图像传感器记录的衍射图样可以表示为
的傅里叶变换,因此,由图像传感器记录的衍射图样可以表示为
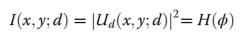
其中,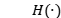 表示将相位对象
表示将相位对象 与测量的衍射模式
与测量的衍射模式 联系起来的映射函数。然后,相位成像问题的目标是建立一个逆映射
联系起来的映射函数。然后,相位成像问题的目标是建立一个逆映射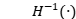 ,
,
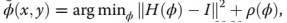
一种典型的方法是尝试从大量的标记数据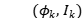 中学习映射函数
中学习映射函数 ,形成训练集。
,形成训练集。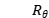 是由一组权重和偏差定义的神经网络的映射函数,训练过程产生了一个可行的映射函数
是由一组权重和偏差定义的神经网络的映射函数,训练过程产生了一个可行的映射函数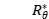 ,它可以将一个不在ST中的衍射图样
,它可以将一个不在ST中的衍射图样 映射到相应的阶段
映射到相应的阶段 ,即
,即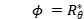 。在这里提出的物理网络模型中,该阶段的检索被表述为:
。在这里提出的物理网络模型中,该阶段的检索被表述为:
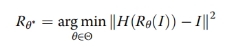
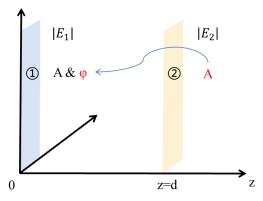
图 12 基于衍射神经网络的相位反演示意图
已知两个平面上电场的幅度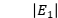 、
、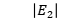 ,使用物理增强深度神经网络通过
,使用物理增强深度神经网络通过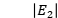 反演出
反演出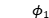 ,在1平面上电场幅度相位都已知。具体步骤如下:
,在1平面上电场幅度相位都已知。具体步骤如下:
a) 通过①平面的电磁波,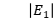 已知,
已知,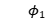 待求
待求
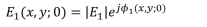
b) 到达②平面的电磁波可以由①平面的电磁波推演
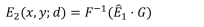
c) 在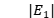 确定的条件下,
确定的条件下,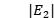 只取决于
只取决于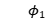
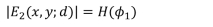
d) 由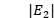 反演
反演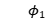
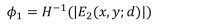
e) 确定机器学习的优化函数
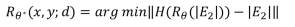
总的来说,基于衍射神经网络的相位反演算法是一种创新技术,能够在许多实际应用中实现高效且精确的相位恢复。未来,随着深度学习技术和计算资源的不断进步,基于衍射神经网络的相位反演算法有望在更多领域得到应用,如何有效地减少数据需求和提高计算效率也是研究的重点方向。
参考文献
[1] CHEN K-S. Principles of Synthetic Aperture Radar Imaging [M]. Taylor and Francis;CRC Press.
[2] TOWNSEND P A. Principles and Applications of Imaging Radar: Manual of Remote Sensing [J]. Ecological Engineering, 2000, 16(2): 309-11.
[3] 何国瑜. 电磁散射的计算和测量 [M]. 电磁散射的计算和测量, 2006.
[4] 赵敏, 栾宇哲, 朱羽晞, et al. 不确定参数目标电磁散射特性计算及评估 [J]. 电波科学学报: 1-15.
[5] 王闻岩, 左炎春, 吕冰, et al. 外场条带式散射成像系统研究; proceedings of the 2023年全国微波毫米波会议, 中国山东青岛, F, 2023 [C].
[6] 王化宾, 何渝, 赵立新. 基于改进Gerchberg-Saxton算法的全息双面光刻方法 [J]. 激光与光电子学进展, 2023, 60(16): 69-75.
[7] 马骁, 陈椿元, 冯泽心. 相位恢复的蒙日-安培方程与迭代角谱复合型方法 [J]. 激光与光电子学进展, 2024, 61(05): 255-62.
[8] 杨立铖, 洪涛, 杨博光, et al. 基于非凸优化方法的无相位天线平面近场测量方法; proceedings of the 2023年全国天线年会, 中国黑龙江哈尔滨, F, 2023 [C].
[9] New York University; NYU’s LeCun wins Turing Award for breakthroughs in artificial intelligence [J]. NewsRx Health & Science, 2019.
[10] 张文悦, 贾子彦, 李青, et al. 基于ResNet和UNet的胃癌病理图像诊断系统 [J]. 河北大学学报(自然科学版): 1-8.
[11] 黎昕然, 陈嘉杰, 王美婷, et al. 深度学习赋能的结构光照明超分辨显微技术:原理与应用 [J]. 中国激光: 1-28.
[12] 张洪峰, 孙沛叶, 刘俊培, et al. TF-Net:一种优化泰勒公式模块的图像去噪算法研究 [J]. 中国信息界, 2024, (03): 235-40.
[13] 陈施宇, 金鑫, 习修良, et al. 基于Transformer和生成对抗网络的多聚焦图像融合 [J]. 云南大学学报(自然科学版): 1-11.
[14] FEI W, YAOMING B, HAICHAO W, et al. Phase imaging with an untrained neural network [J]. Light, science & applications, 2020, 9(1): 77.