《高频散射发展报告》
高频散射发展报告
引言
随着现代科学技术的快速发展,高频散射理论作为电磁波散射理论的重要分支,已经深入到工程实践的方方面面,特别是在雷达、通信和天线设计等领域,随着应用需求的不断增加,高频散射的研究也在不断深化和拓展。
根据散射体尺寸和波长的关系,散射方式可分为低频散射(瑞利区)、谐振散射(谐振区)和高频散射(光学区)。高频散射通常在电磁波的波长远小于物体特征尺寸的情况下,电磁波遇到物体表面时发生的反射、折射和绕射现象。散射现象可以通过麦克斯韦方程组来描述,但对于复杂的几何形状和材料特性,直接求解麦克斯韦方程组往往非常困难,需要借助近似理论和数值方法来进行分析和求解。
20世纪初,科学家们开始了对电磁波传播和散射现象的研究,逐步建立起一套系统的电磁散射理论,其中高频散射理论作为重要组成部分,得到了广泛的关注和研究。高频散射涉及波长较短、频率较高的情况下,经典电磁理论无法准确描述电磁波的行为,此时需要引入几何绕射理论(Geometric Theory of Diffraction GTD)[1]、几何光学(Geometrical Optics, GO)[2]、物理光学(Physical Optics, PO)[3]、一致性绕射理论(Uniform Theory of Diffraction, UTD)[4-6]等高频散射理论,以便更准确地分析和预测电磁波的传播和散射特性。
随着计算机技术的发展,高频散射的数值方法也得到了广泛应用,如有限差分法(Finite-Difference Time-Domain, FDTD)[7]、有限元法(Finite-Difference Time-Domain, FEM)[8]、矩量法(Method of Moments, MoM)[9, 10]、多层快速多极子技术算法(multilevel fast multipole algorithm, MLFMA)[11]等,这些数值方法能够充分发挥计算机的优势,处理复杂的电磁波散射问题,并为实际工程应用提供有力的支持。
高频散射理论被应用在诸多领域:雷达系统通过发射电磁波并接收目标散射回来的回波信号,实现对目标的探测和识别,准确描述电磁波在目标表面的散射现象,对于提高雷达系统的探测性能至关重要;在天线设计中,天线作为通信系统的关键组件,其性能直接影响到通信质量,通过高频散射理论的分析和优化设计,可以显著提高天线的辐射效率和方向性;随着通信频率的不断提升,高频散射理论可以为通信系统的设计和优化提供重要的理论支持。
随着新材料和新技术的发展,特别是人工电磁材料和镀膜技术的出现,高频散射理论迎来了新的挑战和机遇,传统的散射理论在处理新材料的散射问题时存在局限性,需要发展新的理论和方法;同时,基于大数据和人工智能的高频散射研究也逐渐成为新的研究热点,为未来的发展提供了新方向。
本报告将全面介绍高频散射的基础理论,详细讨论这些理论的发展历程、基本原理及其应用,同时查阅几篇高频散射方向的文献,以便全面了解高频散射方法的最新进展和新方法。
一、 高频散射的基础理论
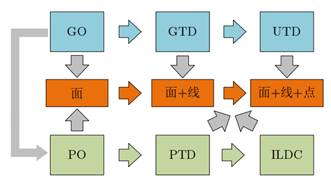
图 1 高频散射发展历程示意图
1. 几何光学(GO)
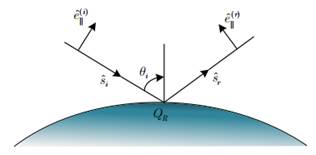
图 2 几何光学示意图
几何光学法主要适用于波长较短,而物体尺寸较大的情况,在这种条件下,电磁波可以近似为沿直线传播的射线,它的核心在于忽略了波的衍射效应,只考虑了波的反射和折射。这种方法基于几个基本假设:射线沿直线传播,不发生弯曲;当射线遇到物体表面时,遵循反射定律,即入射角等于反射角;折射现象也遵循斯涅尔定律,即入射角与折射角的正弦比等于两种介质的折射率比。GO电场可以表示为
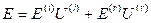
其中,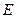 为总场,
为总场,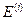 为入射场,
为入射场,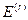 为反射场,
为反射场,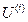 、
、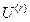 为阶跃函数,其分别在有入射场、反射场的区域等于1,没有时等于0。
为阶跃函数,其分别在有入射场、反射场的区域等于1,没有时等于0。
几何光学通常用于计算雷达散射截面,可以提供快速的计算结果,但可能无法准确描述波的衍射和干涉效应,这些效应在波长与物体尺寸相近或更小的情况下变得显著。
2. 几何绕射理论 (GTD)
几何绕射理论由Keller在20世纪50年代提出,基于几何光学的基本原理,假设电磁波在传播过程中,可以看作是一系列光线,这些光线在遇到物体边界时,会发生反射、折射和绕射等现象,通过引入绕射系数,克服了在阴影区域0场强的问题。
GTD得到的场的表达式为
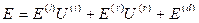
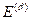 为绕射场。绕射系数描述了电磁波在物体边界上的绕射特性,其计算依赖于物体的几何形状和材料特性,对于简单的几何形状——平面、圆柱、边和球体等——绕射系数可以通过解析方法来求解,但对于复杂的几何形状,绕射系数的计算则需要借助数值方法。
为绕射场。绕射系数描述了电磁波在物体边界上的绕射特性,其计算依赖于物体的几何形状和材料特性,对于简单的几何形状——平面、圆柱、边和球体等——绕射系数可以通过解析方法来求解,但对于复杂的几何形状,绕射系数的计算则需要借助数值方法。
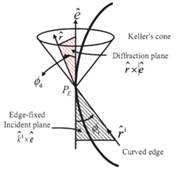
图 3 绕射锥几何体的曲面尖劈绕射
几何绕射理论在处理复杂几何形状的电磁波散射问题时具有很大优势。通过引入绕射系数,可以将复杂的边界条件转换为简单的几何光学问题,不需要对目标表面的感应电流进行积分,从而简化了问题的求解,但在处理一些边界条件复杂的散射问题时,GTD的原始表达式在射线阴影边界和焦散位置存在奇异现象,即不连续性。
3. 一致性理论 (UTD)
一致性绕射理论由Pathak和Burke等人在20世纪70年代提出,是为克服几何绕射理论在处理复杂边界条件时的局限性,在其基础上发展起来的一种更为精确的高频散射理论。
通过考虑物体表面上的电流分布和边界条件来修正绕射系数,使理论计算更加准确。通过引入菲涅耳函数将劈尖边绕射推广到在阴影边界处也连续的情况,得到了广泛适用于任意金属劈尖边的表达式,通过将表达式中的参数取特殊值可以退化为其他任意情况下的劈尖边散射。
与几何绕射理论相比,一致性绕射理论在处理复杂几何形状和边界条件时,表现出显著的优势,在许多领域得到了广泛应用,如天线罩的设计和优化、雷达目标的识别和跟踪等。
4. 物理光学 (PO)
物理光学可以通过对物体表面的电流分布进行积分来求解散射场,将物体表面划分为若干小面元,每个面元上的电流分布可以看作是一个点源,这些点源在空间中产生的次级波叠加起来,就构成了散射场。
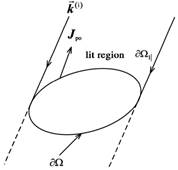
图 4 PEC散射体上的PO电流
物理光学的基本思想就是将电磁场分解为入射场和散射场两部分,入射场是自由空间中的电磁波,散射场是物体表面产生的次级波。物理光学被公认在高频电磁场计算领域具有极佳的适用性,特别对电大尺寸目标的散射及辐射问题能够给出满意的结果,表现出较高的计算精度,主要缺点是不能计算散射体上不连续的几何结构处产生的感应电流,不考虑多次散射。
5. 高频散射的数值方法
随着计算机技术的发展,高频散射的数值方法得到了广泛的应用。数值方法能够处理复杂的电磁波散射问题,并为实际工程应用提供有力的支持,常用的数值方法包括有限差分法、有限元法和矩量法等。
有限差分法是一种时域数值方法,通过将空间和时间离散化,进而求解麦克斯韦方程组,优点是可以直接处理时域问题,适用于宽频带和瞬态问题的分析,在处理大尺度目标的散射问题时,表现出较高的计算效率和精度。但在处理小尺度和复杂边界条件下,存在一定的局限性。
有限元法是一种基于变分原理的数值方法,通过将求解区域划分为若干小的有限元,并在每个元素上使用局部多项式基函数来近似解,然后通过组装全局矩阵来求解整个系统的线性方程组。有限元法的优点是可以处理复杂的几何形状和材料特性,特别适用于处理非均匀介质和复杂边界条件的散射问题,但需要非常细的网格来捕捉高频波的快速变化,从而增加了计算量。
矩量法是通过将边界条件或介质内部的散射问题转化为积分方程,利用基函数和测试函数来近似这些积分方程。矩量法的优点是可以处理复杂的边界条件和电流分布,特别适用于处理高频散射问题,因为其可以通过使用快速多极子方法等技术来减少计算量,并且可以利用高频近似来简化问题。
多层快速多极子技术通过将问题分解为多个层次,每个层次对应不同尺度的子问题,然后利用多极子展开技术来近似远场相互作用,从而显著减少计算量和内存需求,使得大规模电磁问题的求解成为可能,在处理复杂结构和高频应用时能够凸显其优越性。
但前面提到的这几种数值方法对计算能力的依赖性高,随着目标的电尺寸的增大,计算量会迅速增大,故对电大尺寸目标和大场景的散射计算代价高。[12]
二、 最新研究进展
下面搜索了一些高频散射方向的论文,对其中用到的方法进行总结整理,全面了解高频散射方法的最新进展和新方法。
1. 《典型几何基元的高频散射建模方法梳理》

图 5 论文中提到的建模图形
这篇文献梳理了典型几何基元的高频散射建模方法,包括面散射、线散射和点散射等,适用于高分辨率SAR图像中目标与环境的电磁散射机制研究。提出了从几何基元出发,发展对应的散射基元,通过散射基元的组合和相互作用实现散射特征的表征,讨论了构建散射机制字典的可行性,以支持SAR图像散射信息的解译。[13]
2. 《解决电磁散射问题的现代高频技术》
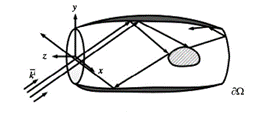
图 6 使用SBR方法的腔体多次反射示意图
这篇文献首先对解决电磁散射问题的现代高频方法的研究进展进行了综述,特别提到了SBR方法,并提出了数值最速下降路径法来计算高频散射场。接着,文章综合讨论了高频驻相点贡献、凯勒锥以及爬行波场等关键技术。[14]
3. 《任意多边形导体板的高频散射分析》
这篇文献研究了任意多边形导体板在高频散射情况下的特性,通过结合微分长度绕射系数和一致性等效电磁流的概念,推导出了微分边缘绕射系数,并利用这个系数,将任意观察方向上的远区散射场与任意方向入射的平面波联系起来,特别适合于复杂目标的高频散射分析。
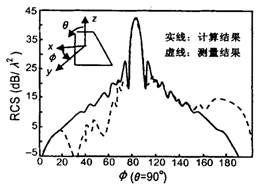
图 7 使用文中方法计算的梯形板散射截面
文章还通过对矩形平板、梯形板和任意多边形板的散射截面的计算和实验数据的比较,展示了该方法在不同形状导体板上的应用效果,并且提出了进一步分析原因和改进精度的必要性。[15]
4. 《高频散射问题的高效配置法》
这篇文献利用积分方程方法和配置法研究了二维高频散射问题,主要研究了二维声软高频散射问题的数值模拟方法,从边界积分方程出发,利用密度函数在凸区域外散射的渐近分析,将高振动态问题转化为低振动态问题。
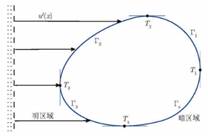
图 8 文中使用的高效配置法的障碍物示意图
通过选择合适的积分区间和配置点,提出了一种高效的配置法,并通过数值例子展示了该方法的有效性。这种方法在保持高精度的同时,减少了对波数的依赖性,对于解决高频散射问题具有重要的理论和实际意义。[16]
5. 《电磁散射高频方法的加速计算研究和系统实现》
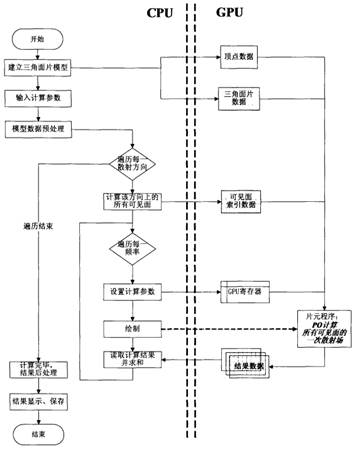
图 9 CPU同GPU交互流程图
这篇文献专注于电磁散射高频方法的加速计算研究,基于高频电磁估算理论,研究了镜面反射和多次反射这两种散射源的计算方法,采用了物理光学法和几何光学法相结合的方法来计算多次散射场。同时提出了并行计算的方法,利用GPU和集群计算平台的优势,设计了基于GPU和基于微机集群的电磁散射算法,通过实验结果的性能和误差分析,验证了这些方法在解决大规模电磁散射计算问题方面的有效性。[17]
6. 《外形隐身目标雷达散射截面高频散射特性的研究》
这篇文献主要研究了外形隐身技术对雷达散射截面的影响,首先分析了高频散射机理,提供了简单形体外形隐身的理论依据,介绍了高频散射场的计算方法,包括几何光学法、物理光学法等,并讨论了镜面反射、边缘衍射等主要的高频散射机理。
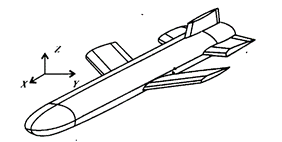
图 10 文中使用的飞航导弹模型
文章还提供了一个复杂飞航导弹模型的RCS计算案例,展示了如何将导弹分解为不同部件并应用不同的高频方法进行计算,通过计算结果与测量结果的对比,验证了所提方法的有效性,该研究对于隐身技术的发展和应用具有重要的理论和实践价值。[18]
7. 《各向异性材料涂覆目标电磁散射高频算法与散射特性仿真的软件实现》
这篇文献探讨了各向异性介质涂覆在电大尺寸复杂目标上的电磁散射高频算法,提出了各向异性介质涂覆无限大理想导电体平板散射场的多模射线解和谱域法解,这些方法为复杂目标的电磁散射预估提供了理论基础和计算方法。此外,文章还设计了一个能够对各向异性介质涂覆的复杂目标进行高频散射特性仿真的软件,通过对软件的验证和算例分析,证明了所提出方法的有效性和准确性。[19]
三、 高频散射的应用
高频散射理论在许多工程领域得到了广泛应用,发挥着不可替代的作用,下面列举了几个典型案例。
在军事和国防领域,高频散射技术主要用于雷达目标识别,通过对目标的电磁散射特性进行分析,提高雷达对不同目标的识别能力。此外,高频散射技术也被用于电子战和隐身技术,帮助设计能够最小化雷达散射截面的军事装备。[20]
在地球物理学中,高频散射理论被应用于数值模拟和反演成像,以研究地球内部结构和地质特征,这种方法能够提供关于地壳和地幔特性的详细信息,对于地震预测、资源勘探和地质构造分析等领域具有重要价值。[21]
在航空航天领域,高频散射技术被用于分析飞行器在高速飞行时的电磁散射特性,有助于优化飞行器设计,减少雷达探测到的信号,提高其隐身性能,也被用于航天器的轨迹优化和再入大气层时的热防护设计。
合成孔径雷达图像解译是遥感技术中的一个重要方面,高频散射建模方法可以更好地理解和解释SAR图像中的目标和环境特征,这对于灾害监测、环境评估和城市规划等应用至关重要。[13]
通过这些应用,我们可以看到高频散射技术在现代科技和工程中扮演的关键角色,它不仅推动了科学理论的发展,也为实际问题的解决提供了强有力的工具。
四、 高频散射的发展趋势和挑战
尽管高频散射理论在许多领域取得了显著成果,但随着新材料和新技术的发展,特别是人工电磁材料的出现,给高频散射理论带来了新的挑战和机遇。人工电磁材料具有独特的电磁特性,传统的散射理论可能无法准确描述其散射特性,在处理新材料的散射问题时,可能存在一定的局限性,需要发展新的理论和方法来应对这些挑战。
随着计算能力的不断提升,基于大数据和人工智能的高频散射研究逐渐成为新的研究热点,这些计算机技术可以更高效地分析和预测电磁波的散射特性,从而提高系统的性能和可靠性。
高频散射理论在实际工程应用中,仍然面临许多挑战,在复杂环境中,电磁波的传播和散射非常复杂,传统的散射理论和数值方法可能无法满足工程需求,需要结合实际应用需求,设计更加精确和高效的散射理论和数值方法。
五、 结论
高频散射领域有着一系列重要的研究成果,这些理论成果为理解和预测复杂目标的散射特性提供了坚实的基础,不仅推动了高频散射理论的进步,也为实际应用提供了强有力的技术支持。
随着技术的发展和应用需求的增加,未来在高频散射领域的研究将具有至关重要的意义。首先,随着雷达系统向更高频率和更高精度的方向发展,深入研究高频散射理论对提高雷达成像分辨率和目标检测能力至关重要;新型材料和结构的不断涌现,探索这些新材料在高频散射下的特性,将有助于开发更先进的隐身技术和电子战策略;除此,高频散射理论在无线通信、遥感探测以及空间天气预测等领域的应用也有着广阔的前景,未来的研究将为这些领域带来创新的解决方案,为实际工程应用提供更加可靠的数据支持。**
**
参考文献
[1] KELLER J B. Geometrical theory of diffraction [J]. Josa, 1962, 52(2): 116-30.
[2] LOANE J, LEE S. A geometrical optics approximation for refraction at a planar interface between arbitrarily lossy media [J]. Journal of Electromagnetic Waves and Applications, 1987, 1(4): 349-76.
[3] ROEDDER J M. CADDSCAT version 2.3: A high-frequency physical optics code modified for trimmed IGES B-spline surfaces [J]. IEEE Antennas and Propagation Magazine, 1999, 41(3): 69-80.
[4] ALBANI M, CAPOLINO F, CARLUCCIO G, et al. UTD vertex diffraction coefficient for the scattering by perfectly conducting faceted structures [J]. IEEE transactions on antennas and propagation, 2009, 57(12): 3911-25.
[5] ALBANI M, CARLUCCIO G, PATHAK P H. A uniform geometrical theory of diffraction for vertices formed by truncated curved wedges [J]. IEEE Transactions on Antennas and Propagation, 2015, 63(7): 3136-43.
[6] GEOMETRICAL A U. Edge in a Perfectly Conducting Surface [J]. PROCEEDINGS OF THE IEEE, 1974, 62(11).
[7] COIFMAN R, ROKHLIN V, WANDZURA S. The fast multipole method for electromagnetic scattering calculations; proceedings of the Proceedings of IEEE Antennas and Propagation Society International Symposium, F, 1993 [C]. IEEE.
[8] FU W, ZHAO Y, HO S L, et al. An electromagnetic field and electric circuit coupled method for solid conductors in 3-D finite-element method [J]. IEEE Transactions on Magnetics, 2015, 52(3): 1-4.
[9] HARRINGTON R F, HARRINGTON J L. Field computation by moment methods [M]. Oxford University Press, Inc., 1996.
[10] ZHAO Z-H, YE H-X. Sparse matrix canonical grid method for three-dimension rough surface; proceedings of the 2018 International Conference on Microwave and Millimeter Wave Technology (ICMMT), F, 2018 [C]. IEEE.
[11] ZHANG Y, LIN H. MLFMA-PO hybrid technique for efficient analysis of electrically large structures [J]. IEEE Antennas and Wireless Propagation Letters, 2014, 13: 1676-9.
[12] XU F, JIN Y-Q. Bidirectional analytic ray tracing for fast computation of composite scattering from electric-large target over a randomly rough surface [J]. IEEE Transactions on Antennas and Propagation, 2009, 57(5): 1495-505.
[13] 张旭, 徐丰, 金亚秋. 典型几何基元的高频散射建模方法梳理 [J]. 雷达学报, 2022, 11(01): 126-43.
[14] 吴语茂, 金亚秋. 解决电磁散射问题的现代高频技术 [J]. 电波科学学报, 2020, 35(02): 192-204.
[15] 张浩斌 马, 郭陈江,许家栋. 任意多边形导体板的高频散射分析 [J]. 电波科学学报, 2003, (01): 53-6.
[16] 李松华, 冼军, 向淑晃. 高频散射问题的高效配置法 [J]. 中国科学:数学, 2017, 47(05): 651-66.
[17] 姜俊. 电磁散射高频方法的加速计算研究和系统实现 [D], 2006.
[18] 耿方志 吕, 张永新,邓发升. 外形隐身目标雷达散射截面高频散射特性的研究 [J]. 光电技术应用, 2005, (04): 26-8+62.
[19] 姚菁晶. 各向异性材料涂覆目标电磁散射高频算法与散射特性仿真的软件实现 [D], 2013.
[20] 李冶. 雷达目标高频散射特性分析及其识别应用研究 [D], 2020.
[21] 孙建国. 高频渐近散射理论及其在地球物理场数值模拟与反演成像中的应用——研究历史与研究现状概述以及若干新进展 [J]. 吉林大学学报(地球科学版), 2016, 46(4): 1231-59.