实验二 图像复原 实验目的 利用反向滤波和维纳滤波进行降质图像复原,比较不同参数选择对复原结果的影响。
实验内容 (1)利用反向滤波方法进行图像复原;
(2)利用维纳滤波方法进行图像复原。
实验要求 (1)输入图像采用实验1所获取的图像,对输入图像采用运动降质模型,如下式所示
与降值图像相关的参数是:
(2)对每一种方法通过计算复原出来的图像的峰值信噪比,进行最优参数的选择,包括反向滤波方法中进行复原的区域半径
(3)将降质图像和利用最优参数恢复后的图像同时显示出来,以便比较。
实验原理 环境的随机噪声等原因都会使图像产生一定程度的退化,图像退化的典型表现是图像出现模糊、失真,出现附加噪声等。由于图像的退化,使得最终获取的图像不再是原始图像,图像效果明显变差。为此,要较好地显示原始图像,必须对退化后的图像进行处理,恢复出真实的原始图像,首先利用退化现象的某种先验知识,建立退化现象的数学模型,然后再根据退化模型进行反向的推演运算,以恢复原来的景物图像。维纳滤波复原维纳滤波就是最小二乘滤波,它是使原始图像与其恢复图像之间的均方误差最小的复原方法。
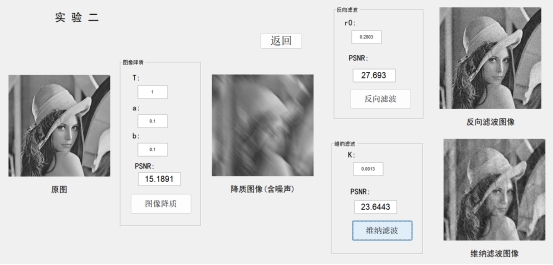
实验结果与分析 实验结果:
首先令
保持
保持
对于加入了高斯白噪声(均值为0,方差为0.01)的反向滤波,进行复原的区域半径的最优参数值为
实验分析:
对于没有噪声的情况——反向滤波时,复原的区域半径越接近于1,滤波效果越好,相对标准图像的 PSNR值越高,当复原的区域半径等于1时,完全恢复原图像;维纳滤波时,噪声对信号的频谱密度比值越接近于0,滤波效果越好,相对标准图像的 PSNR值越高,当噪声对信号的频谱密度比值等于0时,完全恢复原图像。
对于有噪声的情况——滤波效果越好对应的复原的区域半径不等于1,噪声对信号的频谱密度比值也不为0。而a和b的改变导致降质模型的改变,所以噪声分布也发生了相应改变,因此维纳滤波复原的效果是不一样的。而反向滤波则受影响不大。
在对同样加入了高斯白噪声的运动降质图像进行复原时,反向滤波复原比维纳滤波复原的效果好。
主要代码 主程序: 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 clc clear all global T a b K;LINA=imread('LENA512.bmp' ); LINA = rgb2gray(LINA); LINA = im2double(LINA); LINA = imnoise(LINA,'gaussian' ,0 ,0.01 ); T = 1 ; a = 0.1 ; b = 0.1 ; [x,y] = size (LINA); N = x; u=-N/2 :1 :N/2 -1 ; v=u'; s=pi *(a*u+b*v); H1=T./s.*sin (s).*exp (-1 *j *s); h1=(s==0 ); H1(h1)=max (max (H1)); fftlena = fftshift(fft2(LINA)); YLINAF = H1.*fftlena; YLINAf0 = abs (ifft2(YLINAF)); YLINAf0 = uint8(255. *(YLINAf0)); imwrite(YLINAf0,'badLINA.bmp' ) LINA=imread('LENA512.bmp' ); LINA = rgb2gray(LINA); Diff = double(LINA)-double(YLINAf0); MSE=sum(Diff(:).^2 )/(512 *512 ); PSNR_badLINA = 10 *log10 (255 ^2 /MSE(1 )); r = 1 ; x_r=round (x*r)-1 ; y_r=round (y*r)-1 ; H_r=ones (x,y)*1000000 ; H_r(ceil (x/2 -x_r/2 ):ceil (x/2 +x_r/2 ),ceil (x/2 -x_r/2 ):ceil (x/2 +x_r/2 )) = H1(ceil (x/2 -x_r/2 ):ceil (x/2 +x_r/2 ),ceil (x/2 -x_r/2 ):ceil (x/2 +x_r/2 )); YLINAF_inv=YLINAF./H_r; YLINAf0_inv=uint8(255. *abs (ifft2(YLINAF_inv))); imwrite(YLINAf0_inv,'divbadLINA.bmp' ) LINA=imread('LENA512.bmp' ); LINA = rgb2gray(LINA); Diff = double(LINA)-double(YLINAf0_inv); MSE=sum(Diff(:).^2 )/(512 *512 ); PSNR_divbadLINA = 10 *log10 (255 ^2 /MSE(1 )); K = 0 ; H_w = (conj (H1).*H1 + K) ./ (conj (H1).*H1) .* H1; YLINAF_k=YLINAF./H_w; YLINAf0_k = uint8(255. *(abs (ifft2(YLINAF_k)))); imwrite(YLINAf0_k,'kbadLINA.bmp' ) LINA=imread('LENA512.bmp' ); LINA = rgb2gray(LINA); Diff = double(LINA)-double(YLINAf0_k); MSE=sum(Diff(:).^2 )/(512 *512 ); PSNR_kbadLINA = 10 *log10 (255 ^2 /MSE(1 )); maxr = 0 ; r0 = 0 ; for r = 0.28 :0.0001 :0.30 x_r=round (x*r); y_r=round (y*r); H_r=ones (x,y)*1000000 ; H_r(ceil (x/2 -x_r/2 ):ceil (x/2 +x_r/2 ),ceil (x/2 -x_r/2 ):ceil (x/2 +x_r/2 )) = H1(ceil (x/2 -x_r/2 ):ceil (x/2 +x_r/2 ),ceil (x/2 -x_r/2 ):ceil (x/2 +x_r/2 )); YLINAF_inv=YLINAF./H_r; YLINAf0_inv=uint8(255. *abs (ifft2(YLINAF_inv))); LINA=imread('LENA512.bmp' ); LINA = rgb2gray(LINA); Diff = double(LINA)-double(YLINAf0_inv); MSE=sum(Diff(:).^2 )/(512 *512 ); PSNR_divbadLINA = 10 *log10 (255 ^2 /MSE(1 )) if PSNR_divbadLINA>maxr maxr = PSNR_divbadLINA r0 = r end end maxk = 0 ; k0 = 1 ; for K = 0 :0.00001 :0.002 H_w = (conj (H1).*H1 + K) ./ (conj (H1).*H1) .* H1; YLINAF_k=YLINAF./H_w; YLINAf0_k = uint8(255. *(abs (ifft2(YLINAF_k)))); LINA=imread('LENA512.bmp' ); LINA = rgb2gray(LINA); Diff = double(LINA)-double(YLINAf0_k); MSE=sum(Diff(:).^2 )/(512 *512 ); PSNR_kbadLINA = 10 *log10 (255 ^2 /MSE(1 )) if PSNR_kbadLINA>=maxk maxk = PSNR_kbadLINA k0 = K end end
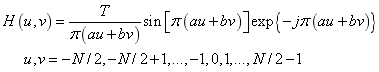
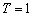 ,
,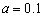 ,
,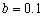 ;
;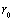 、维纳方法中的噪声对信号的频谱密度比值
、维纳方法中的噪声对信号的频谱密度比值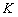 ;
;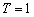 ,
,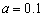 ,
,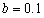 ,加入高斯白噪声(均值为0,方差为0.01)对于反向滤波,设置进行复原的区域半径
,加入高斯白噪声(均值为0,方差为0.01)对于反向滤波,设置进行复原的区域半径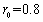 ;对于维纳滤波,设置噪声对信号的频谱密度比值
;对于维纳滤波,设置噪声对信号的频谱密度比值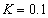 ,实验结果如下,
,实验结果如下,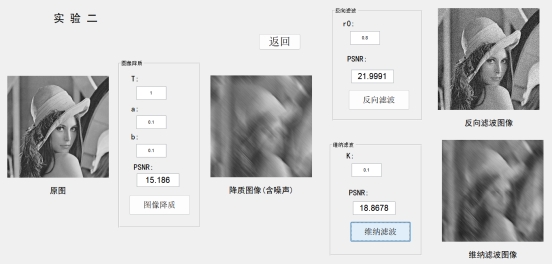
 ,
,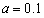 ,
,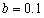 不变,加入高斯白噪声(均值为0,方差为0.01),对于反向滤波,设置进行复原的区域半径
不变,加入高斯白噪声(均值为0,方差为0.01),对于反向滤波,设置进行复原的区域半径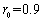 ;对于维纳滤波,设置噪声对信号的频谱密度比值
;对于维纳滤波,设置噪声对信号的频谱密度比值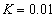 ,实验结果如下,
,实验结果如下,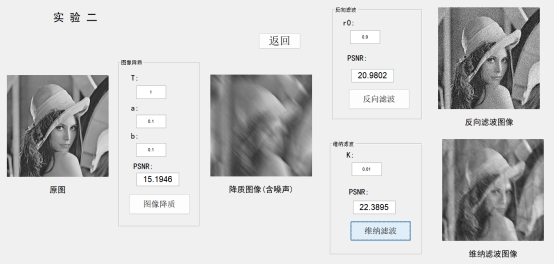
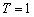 ,
,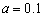 ,
,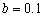 不变,加入高斯白噪声(均值为0,方差为0.01),对于反向滤波,设置进行复原的区域半径
不变,加入高斯白噪声(均值为0,方差为0.01),对于反向滤波,设置进行复原的区域半径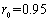 ;对于维纳滤波,设置噪声对信号的频谱密度比值
;对于维纳滤波,设置噪声对信号的频谱密度比值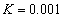 ,实验结果如下,
,实验结果如下,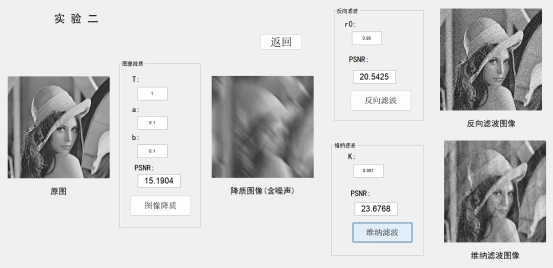
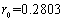 ;对加入了高斯白噪声(均值为0,方差为0.01)的于维纳滤波,噪声对信号的频谱密度比值的最优参数值为
;对加入了高斯白噪声(均值为0,方差为0.01)的于维纳滤波,噪声对信号的频谱密度比值的最优参数值为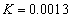 ,实验结果如下,
,实验结果如下,