一、实验目的 1.将一个信号从某一给定的采样率转换到另一不同采样率,即采样率转换。
2.对信号进行滤波。
3.有一个模拟频率为
对上面采样的信号隔点抽取,形成一新的序列,
(1)使用MATLAB自带的播放器进行播放。(注:sound(x,fs))
根据听到的两种不同声音,解释出现这种情况的原因。
(2)根据内插公式(选择合适的
对
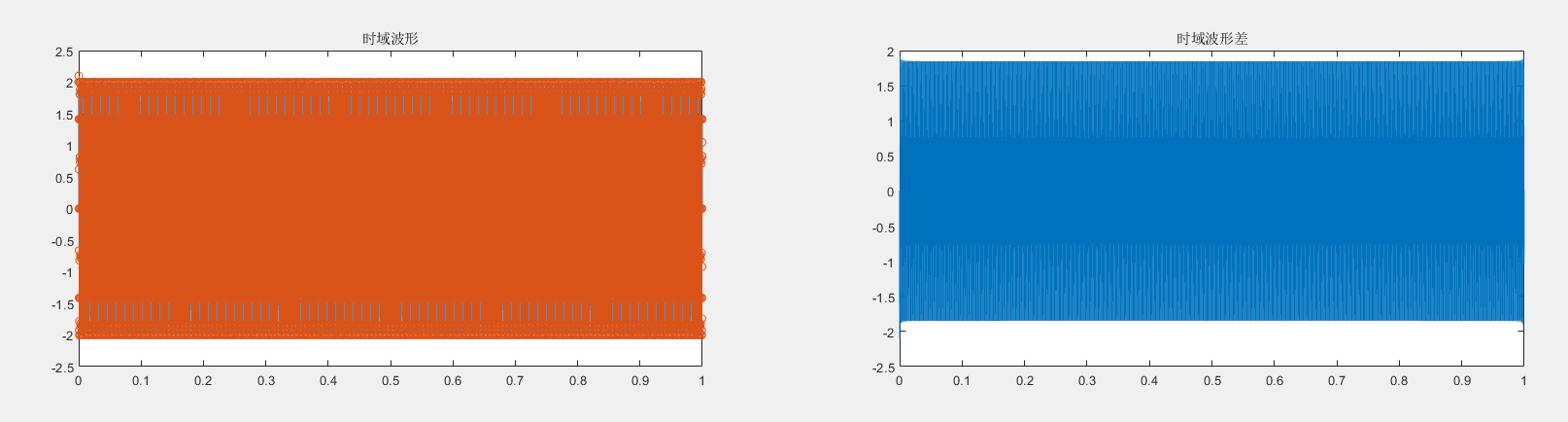
在一张图上,绘制原始信号
绘制原始信号与内插信号的时域波形差。
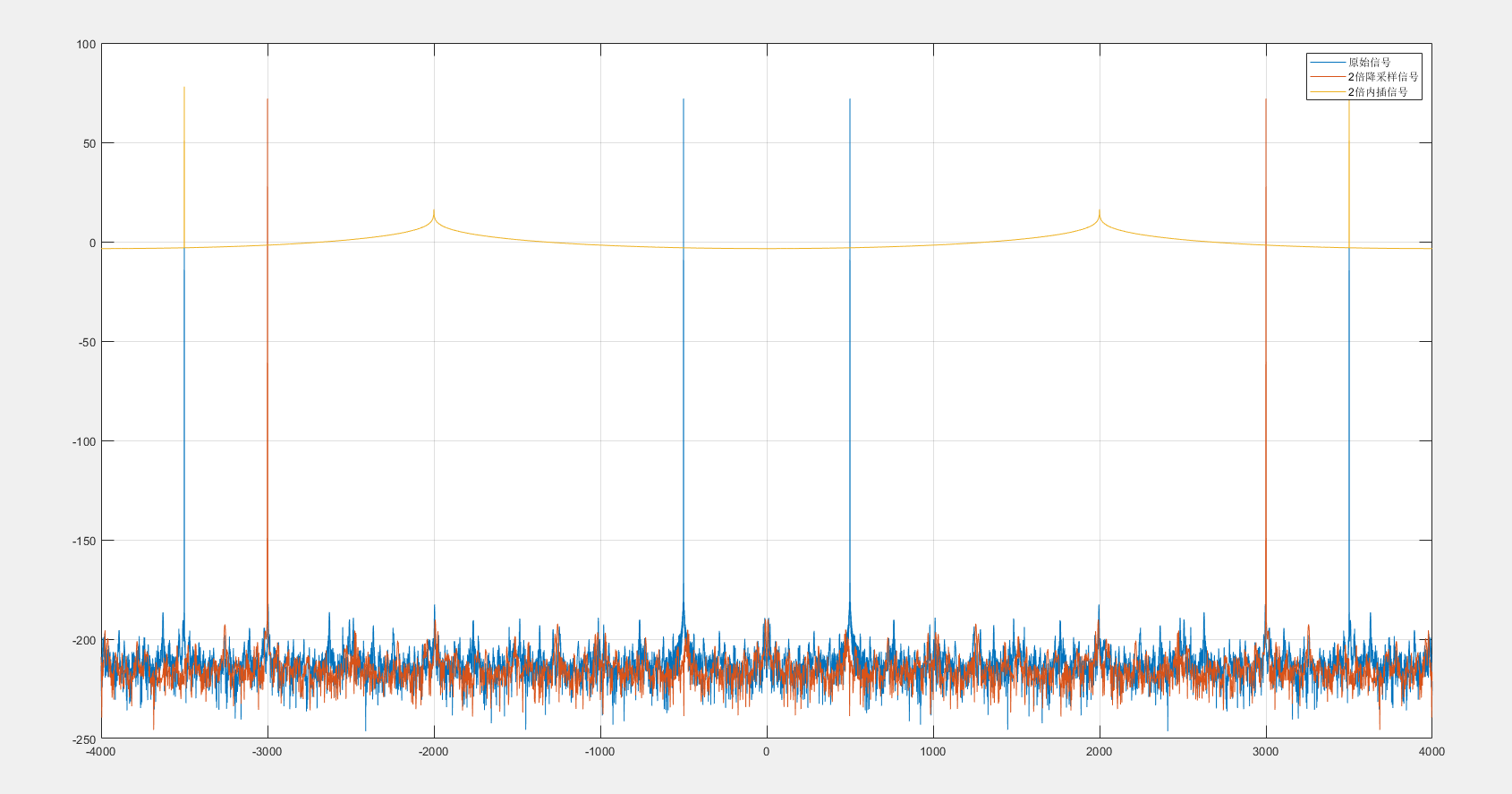
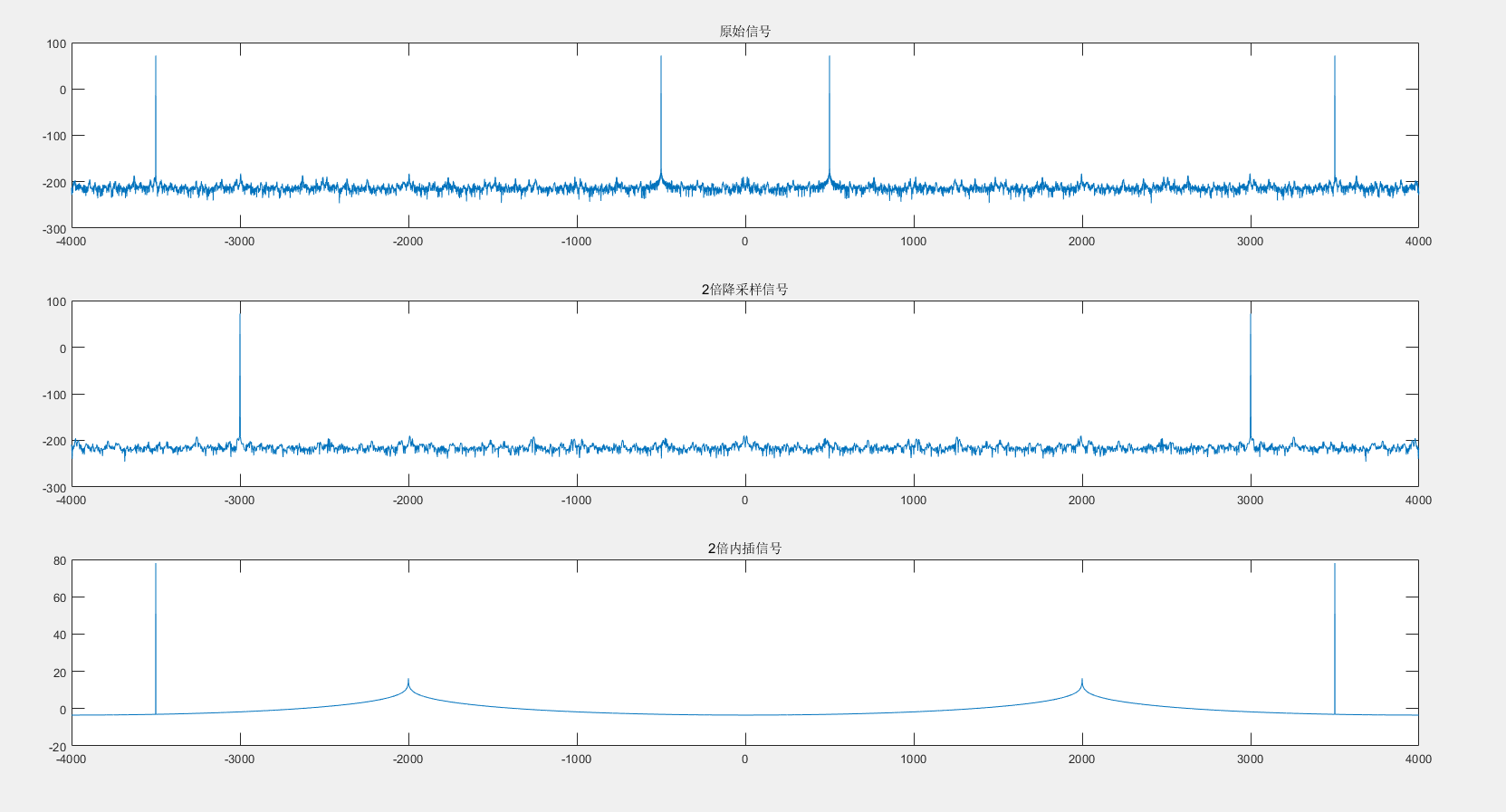
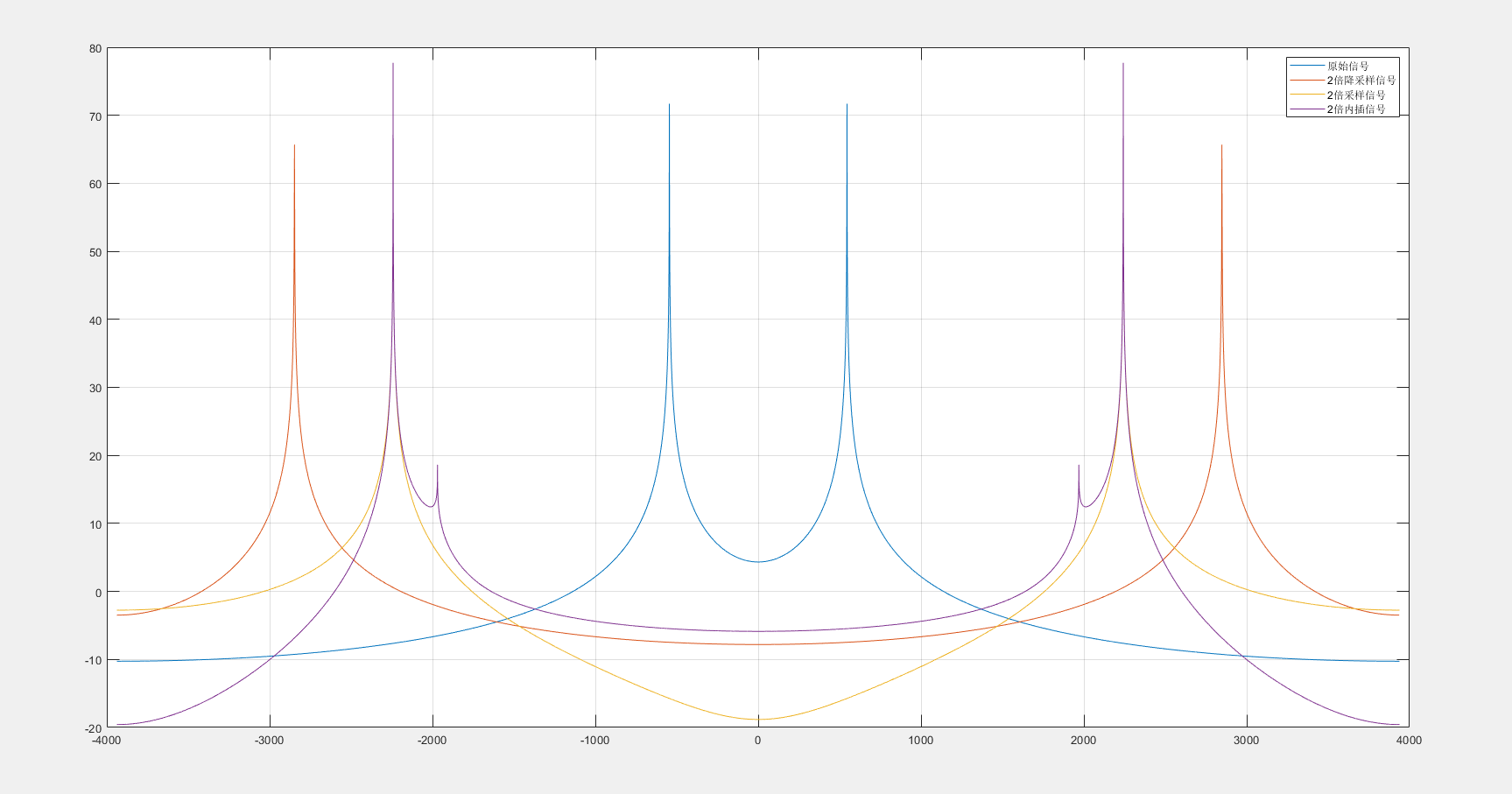
在一张图上,绘制原始信号、2倍降采样信号和内插信号的频谱图。
二、实验原理 滤波器设计与实现是数字信号处理中最基本的内容之一。滤波器分IIR滤波器(无限冲激响应滤波器)和FIR滤波器(有限冲激响应滤波器)两种。
FIR滤波器的设计方法以直接逼近所需离散设计系统的频率响应为基础。FIR滤波器可以很容易地获得线性相移特性,不存在不稳定的问题,是实际系统中广为采用的一种数字滤波器。FIR滤波器的设计,通常有窗函数设计法、频率抽样设计法和最佳逼近设计法。窗函数设计法比较简单,它的频率特性是理想滤波器频谱与窗的频谱的卷积,因而,其频率特性取决于窗的类型和长度。频率抽样设计法比较直观,但由于频域的采样会造成时域的混叠,从而滤波器叠性能不可能很高,为提高滤波器的性能,可以在过渡带加上0~1之间的过渡点。
三、实验条件 1.使用MATLAB及其函数进行实验
四、实验步骤 1.分析问题
2.MATLAB运行
3.分析实验结果
五、实验代码 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 clc clear all f0 = 3500 ; f1 = 500 ; fs = 8000 ; T = 1 /fs; tx = [0 :1 /fs:7999 /fs]; ty = [0 :2 /fs:7999 /fs]; x = cos (2 *pi *f0*tx) + cos (2 *pi *f1*tx); y = cos (2 *pi *f0*ty) + cos (2 *pi *f1*ty); z = zeros (1 ,8000 ); for t = 1 :1 :8000 for j = 0 :3999 if sin (pi *((t-1 )/(2 *fs)-j *T)/T) == 0 && ((t-1 )/(2 *fs)-j *T) == 0 z(t) = z(t) + y(j +1 ); else z(t) = z(t) + y(j +1 )*(sin (pi *((t-1 )/(2 *fs)-j *T)/T)/(pi *((t-1 )/(2 *fs)-j *T)/T)); end end end sound(z,fs*2 ) E = 0 ; for i = 1 :1 :8000 E = E + (z(i )-x(i ))^2 ; end E = E/8000 figure (1 )subplot(2 ,2 ,1 ) plot (tx,x)title('时域波形' ) hold onstem(tx,z) hold onsubplot(2 ,2 ,2 ) plot (tx,x-z)title('时域波形差' ) Xw = fft(x); Yw = fft(y); Zw = fft(z); fredraw = [-4000 /fs:1 /fs:3999 /fs]; freydraw = [-4000 /fs:2 /fs:3999 /fs]; figure (2 )subplot(3 ,1 ,1 ) plot (fredraw*8000 ,20 *log10 (abs (Xw)))title('原始信号' ) hold onsubplot(3 ,1 ,2 ) plot (freydraw*8000 ,20 *log10 (abs (Yw)))title('2倍降采样信号' ) hold onsubplot(3 ,1 ,3 ) plot (fredraw*8000 ,20 *log10 (abs (Zw)))title('2倍内插信号' ) hold onfigure (3 )plot (fredraw*8000 ,20 *log10 (abs (Xw)))hold onplot (freydraw*8000 ,20 *log10 (abs (Yw)))hold onplot (fredraw*8000 ,20 *log10 (abs (Zw)))hold onlegend ('原始信号' ,'2倍降采样信号' ,'2倍内插信号' )grid on
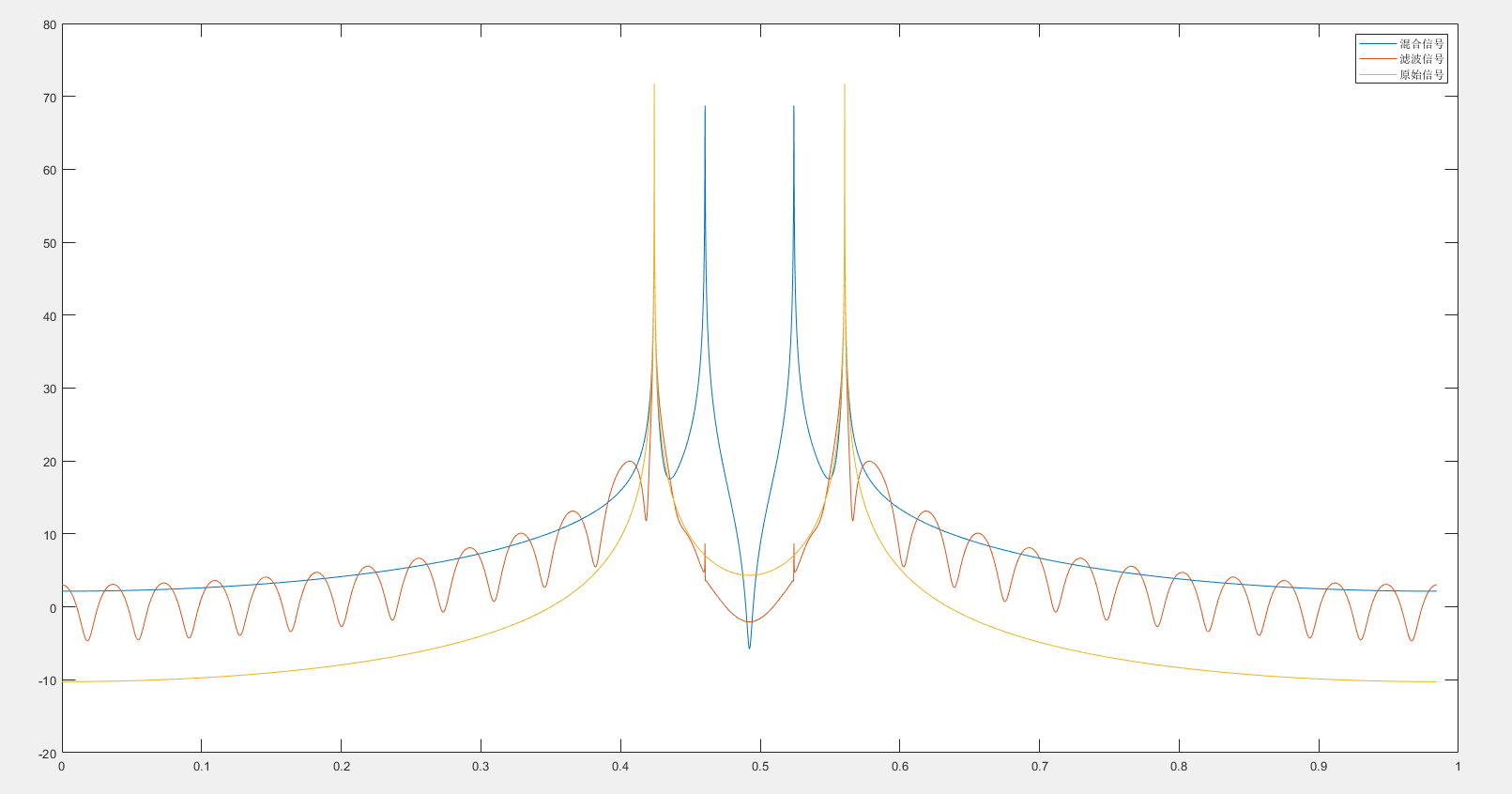
六、实验结果 1.原始信号与内插信号的时域波形相同。
2.采样频率越高,声音越尖锐,这也符合我们对声音音调与频率关系的认知。
七、结果分析 1.重构的效果较为理想,E与M取值相关:M越大E越小,M=1000时,E=0.8745。
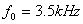 和
和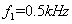 的双频正弦信号,
的双频正弦信号,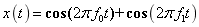 。现以采样率为
。现以采样率为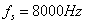 进行采样,得到
进行采样,得到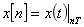 ,
,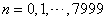
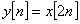
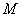 ):
):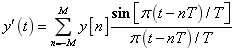
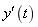 重新以2倍的
重新以2倍的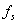 采样得到
采样得到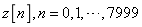 。使用MATLAB自带的播放器进行播放,听听该声音。并统计误差
。使用MATLAB自带的播放器进行播放,听听该声音。并统计误差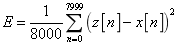
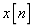 与内插信号
与内插信号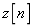 的时域波形。
的时域波形。