一、实验目的 1.将一个信号从某一给定的采样率转换到另一不同采样率,即采样率转换。
2.对信号进行滤波。
3.有一个模拟频率为
设计一个滤波器,提取出频率为
使用MATLAB自带的播放器进行播放,听听
统计滤波信号
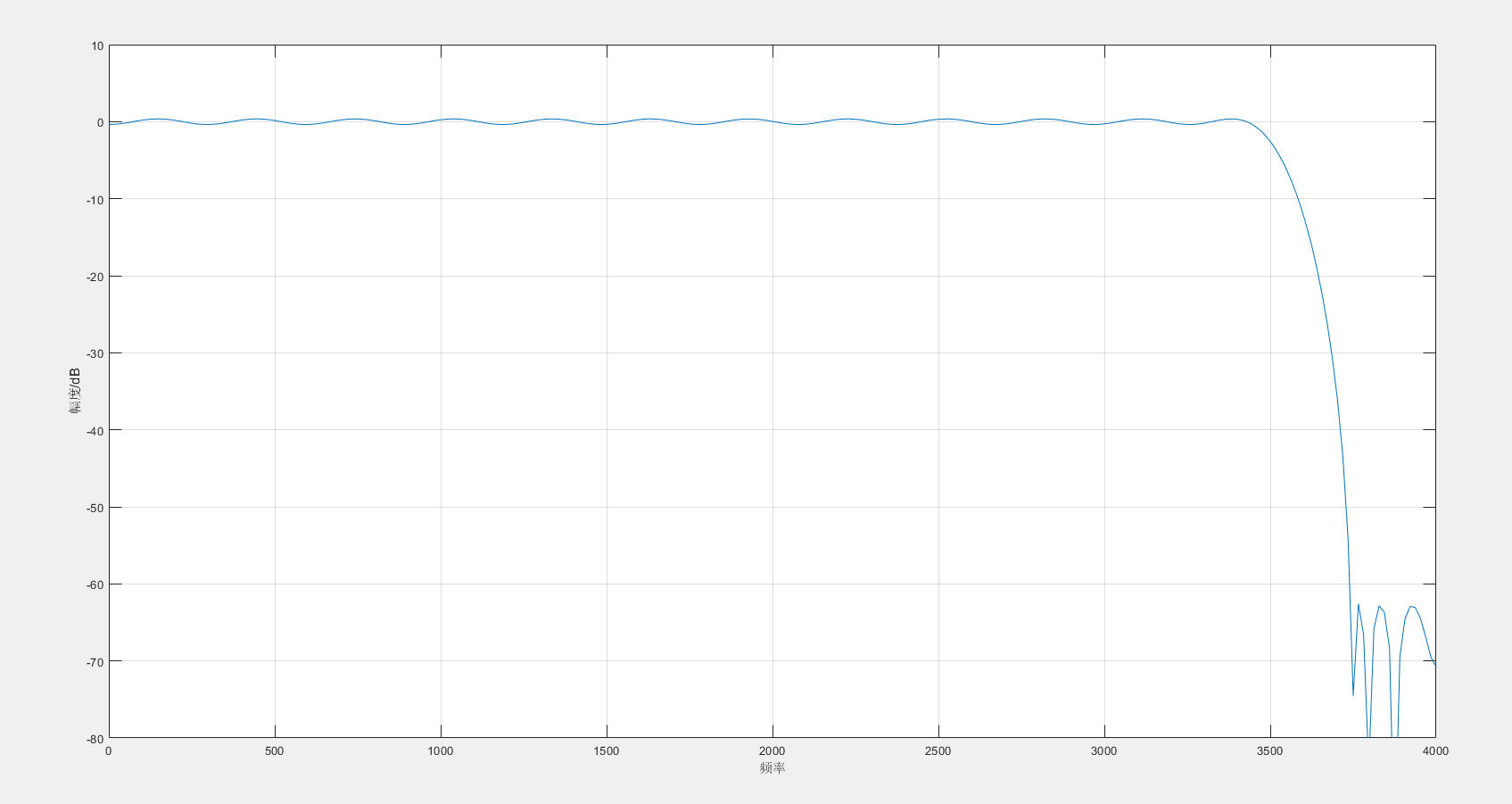
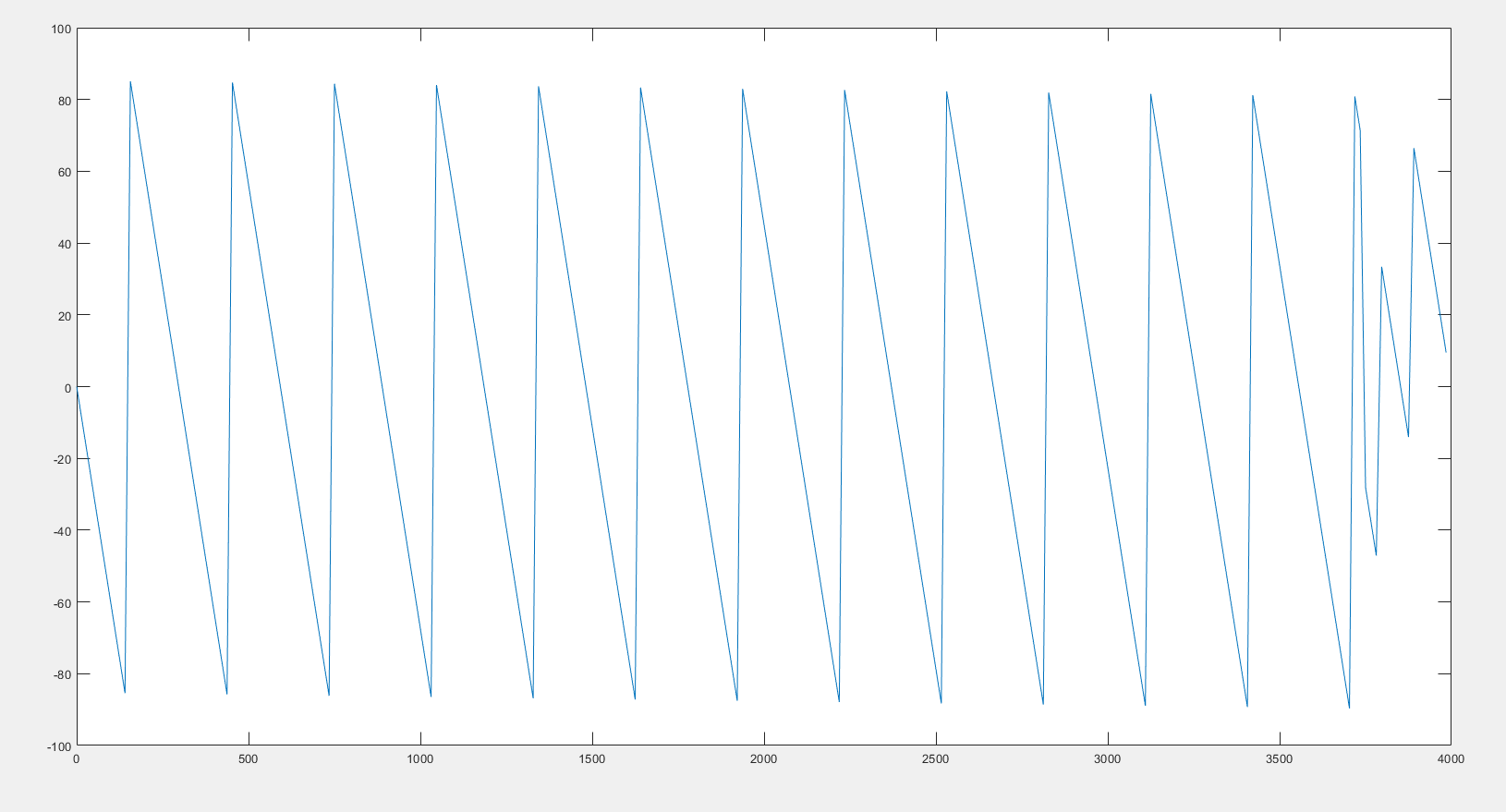
计算滤波器的长度M,绘制滤波器的幅频和相频响应(freqz函数)。
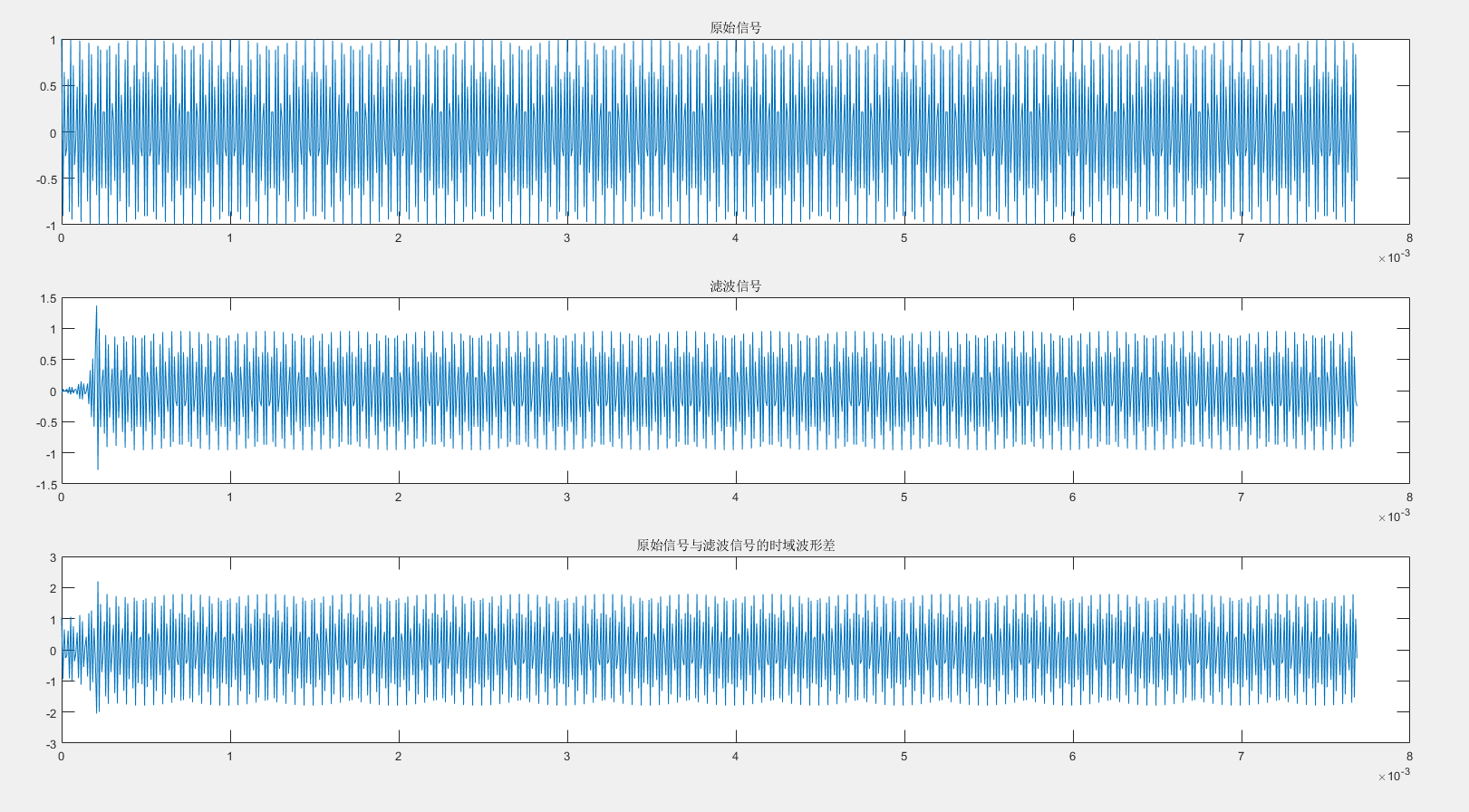
在一张图上,绘制原始信号和滤波信号的时域波形。
绘制原始信号与滤波信号的时域波形差。
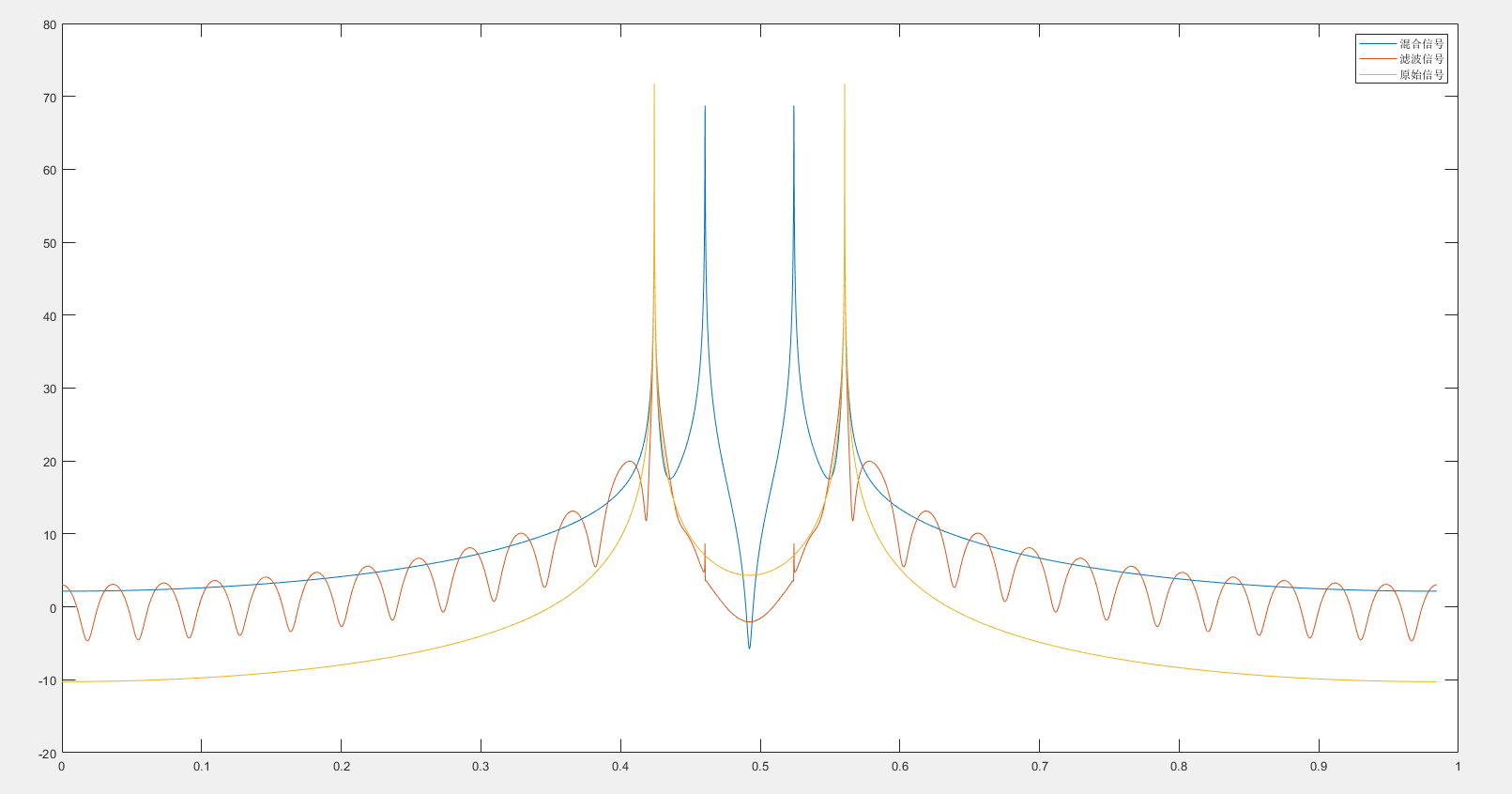
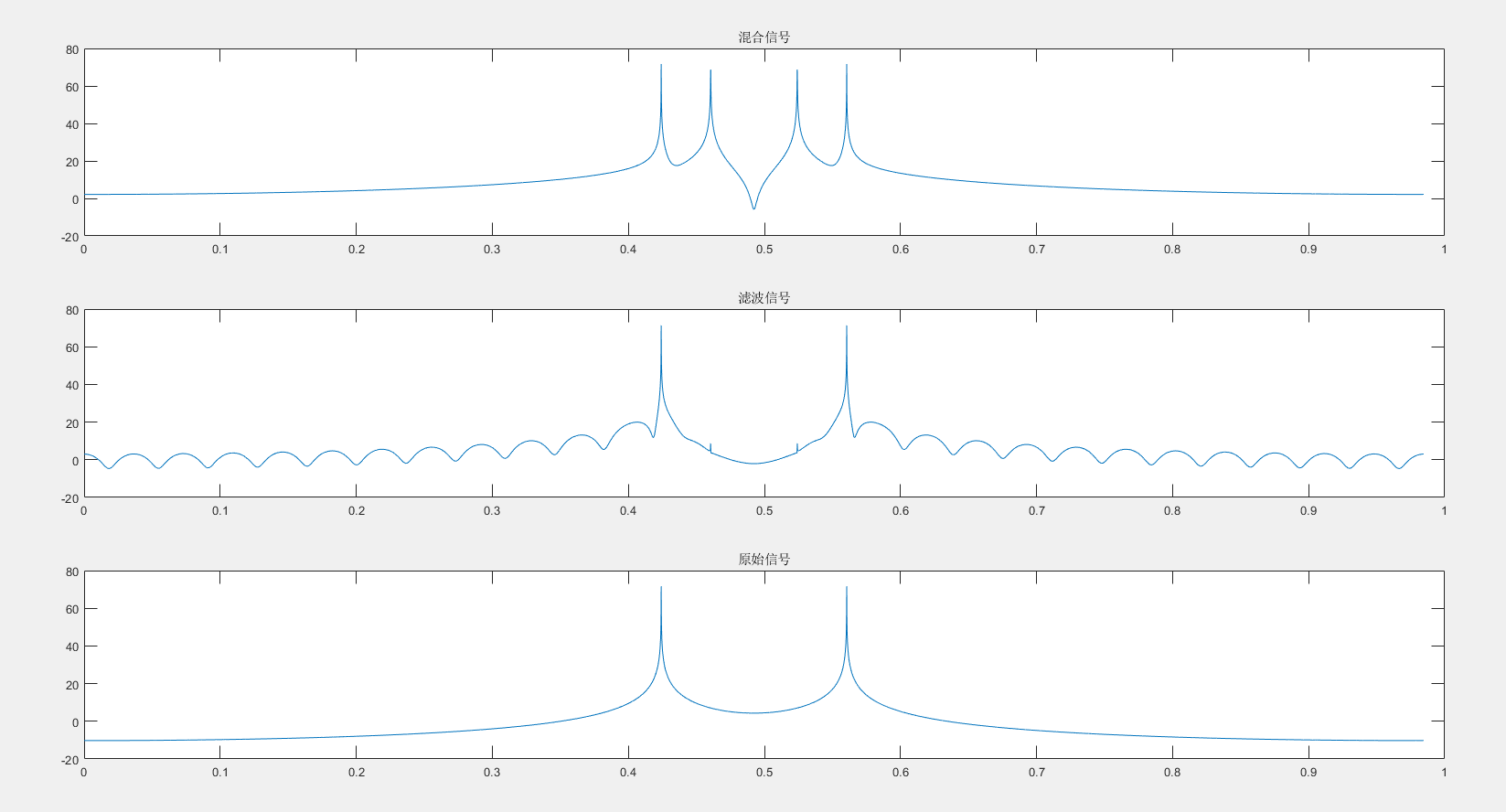
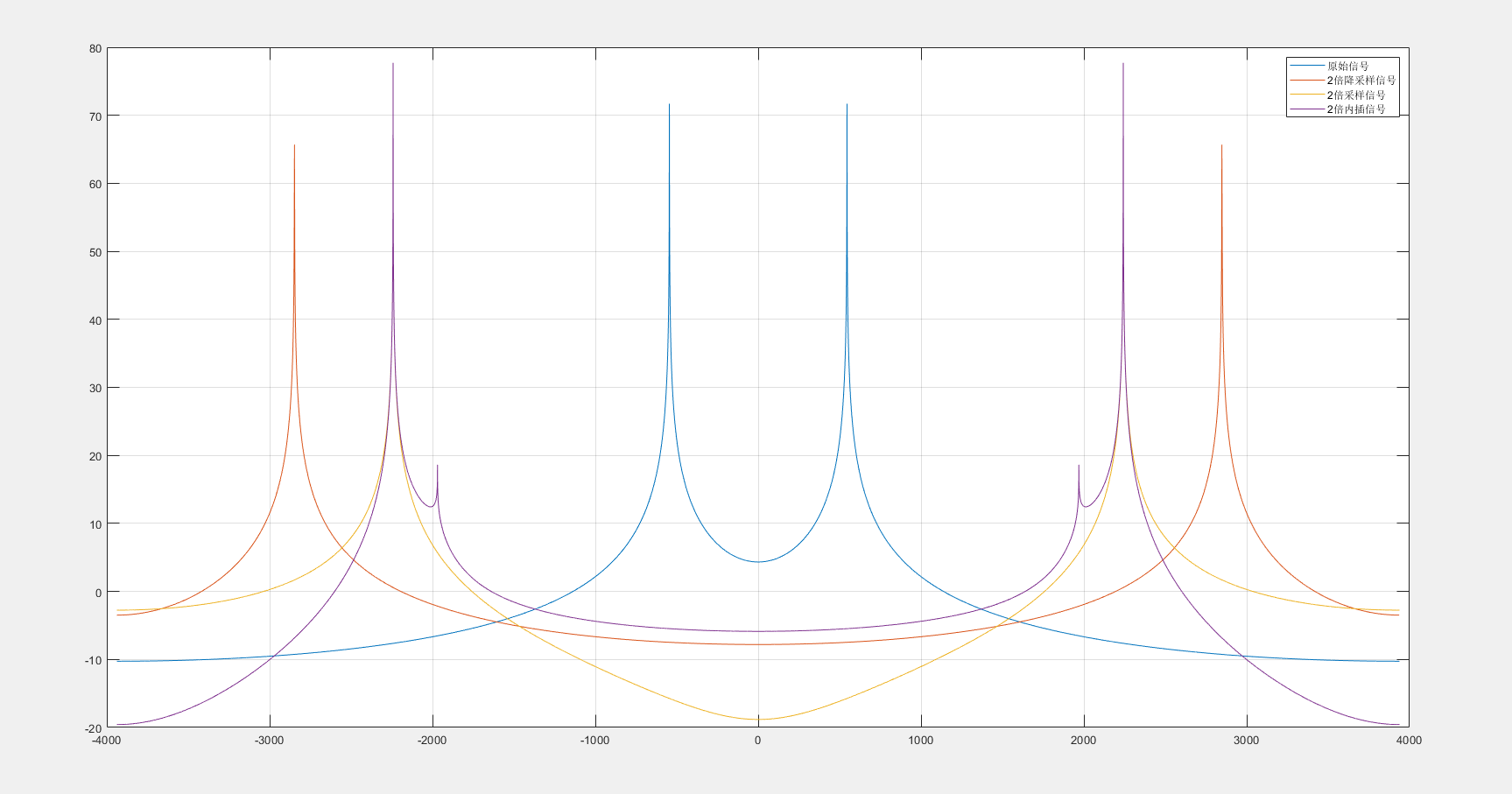
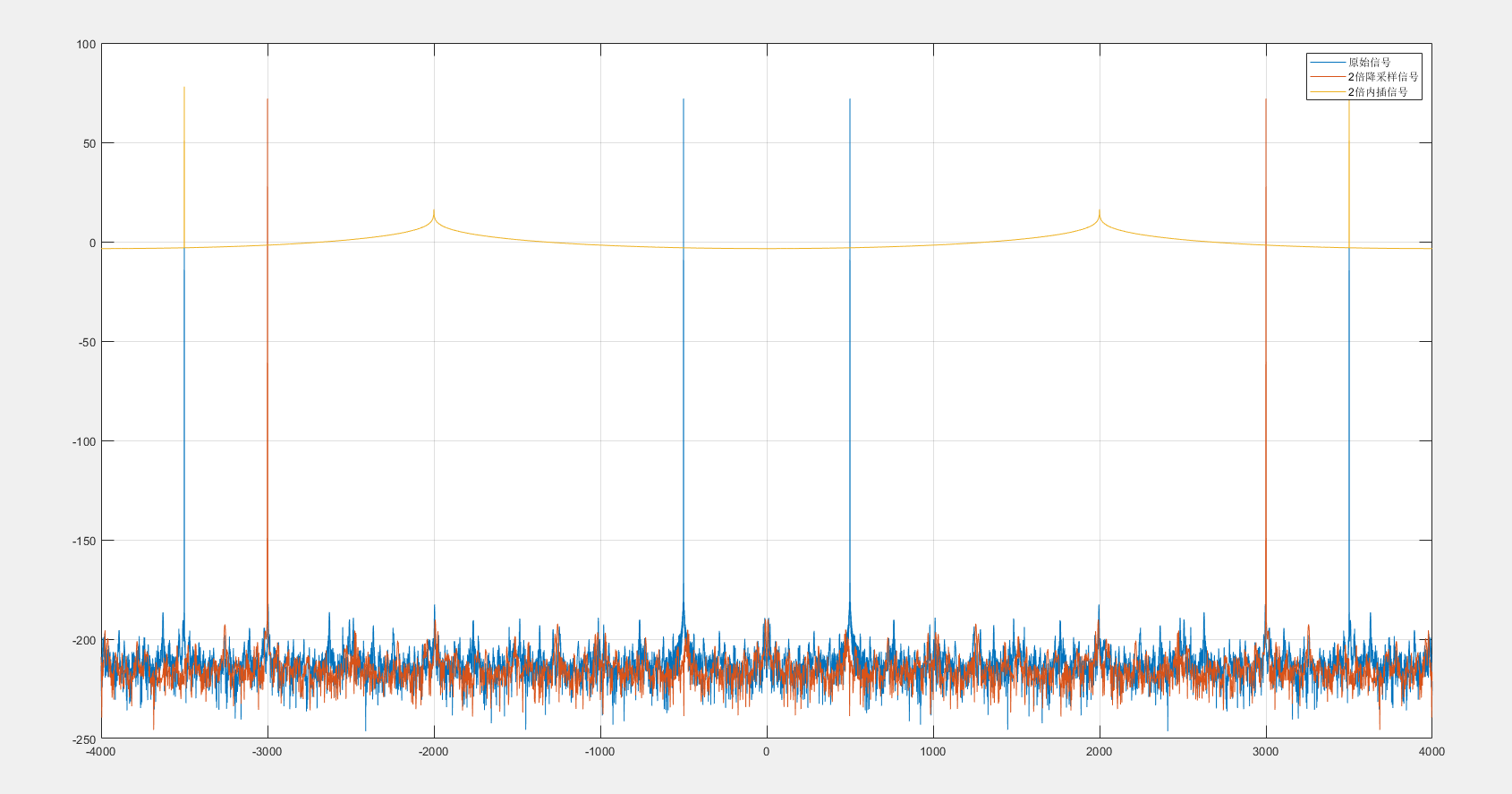
在一张图上,绘制原始信号、混合信号和滤波信号的频谱图;分析在滤波信号中,对干扰信号的抑制是否不低于
将正弦干扰信号的频率分别调整为
二、实验原理 滤波器设计与实现是数字信号处理中最基本的内容之一。滤波器分IIR滤波器(无限冲激响应滤波器)和FIR滤波器(有限冲激响应滤波器)两种。
FIR滤波器的设计方法以直接逼近所需离散设计系统的频率响应为基础。FIR滤波器可以很容易地获得线性相移特性,不存在不稳定的问题,是实际系统中广为采用的一种数字滤波器。FIR滤波器的设计,通常有窗函数设计法、频率抽样设计法和最佳逼近设计法。窗函数设计法比较简单,它的频率特性是理想滤波器频谱与窗的频谱的卷积,因而,其频率特性取决于窗的类型和长度。频率抽样设计法比较直观,但由于频域的采样会造成时域的混叠,从而滤波器叠性能不可能很高,为提高滤波器的性能,可以在过渡带加上0~1之间的过渡点。
三、实验条件 1.使用MATLAB及其函数进行实验
四、实验步骤 1.分析问题
2.MATLAB运行
3.分析实验结果
五、实验代码 主代码:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 clc clear all f0 = 3500 ; f1 = 3800 ; fs = 8125 ; t = [0 :1 /fs:7999 /fs]; t1 = [0 :1 /(16 *fs):7999 /fs]; x = cos (2 *pi *f0*t) + cos (2 *pi *f1*t); x1 = cos (2 *pi *f0*t); Hd = fir; yn = filter(Hd,x); b = Hd.Numerator; xdraw = cos (2 *pi *f0*t1); ydraw = filter(Hd,xdraw); tdelay = [2 /fs:1 /fs:8001 /fs]; xd = cos (2 *pi *f0*tdelay); sum = 0 ; for i =1 :8000 sum = sum + power((yn(i )-xd(i )),2 ); end sum = sum / 8000 figure (1 );[h1,w1]=freqz(b,1 ,'whole' ); plot (w1/pi *4000 ,20 *log10 (abs (h1))); axis([0 ,4000 ,-80 ,10 ]); grid; xlabel('频率' ) ; ylabel('幅度/dB' ) ; figure (2 );grid; xlabel('频率' ) ; ylabel('角度' ) ; plot (w1(1 :256 )/pi *4000 ,angle (h1(1 :256 ))*180 /2 /pi );figure (3 )subplot(3 ,1 ,1 ) plot (t1(1 :1000 ),x1(1 :1000 ))title('原始信号' ) hold onsubplot(3 ,1 ,2 ) plot (t1(1 :1000 ),yn(1 :1000 ))title('滤波信号' ) hold onsubplot(3 ,1 ,3 ) plot (t1(1 :1000 ),x1(1 :1000 )-yn(1 :1000 ))title('原始信号与滤波信号的时域波形差' ) hold onXw = fft(x); Yw = fft(yn); X1w = fft(x1); figure (4 )subplot(3 ,1 ,1 ) plot (t,20 *log10 (abs (Xw)))title('混合信号' ) hold onsubplot(3 ,1 ,2 ) plot (t,20 *log10 (abs (Yw)))title('滤波信号' ) hold onsubplot(3 ,1 ,3 ) plot (t,20 *log10 (abs (X1w)))title('原始信号' ) hold onfigure (5 )plot (t,20 *log10 (abs (Xw)))hold onplot (t,20 *log10 (abs (Yw)))hold onplot (t,20 *log10 (abs (X1w)))hold onlegend ('混合信号' ,'滤波信号' ,'原始信号' )
fir函数:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 function Hd = fir Fs = 8125 ; Fpass = 3500 ; Fstop = 3800 ; Dpass = 0.057501127785 ; Dstop = 0.001 ; dens = 20 ; [N, Fo, Ao, W] = firpmord([Fpass, Fstop]/(Fs/2 ), [1 0 ], [Dpass, Dstop]); b = firpm(N, Fo, Ao, W, {dens}); Hd = dfilt.dffir(b);
六、实验结果 1.设计的滤波器的幅频响应和相频响应符合要求。
2.滤波器对混合信号的处理效果很好。
3.通过滤波器的声音频率更高,与预期相符。
七、结果分析 1.设计的低通滤波器,使3.5kHz的频率分量可以通过,而抑制3.8kHz的频率分量。
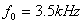 的正弦原始信号,和一个模拟频率为
的正弦原始信号,和一个模拟频率为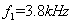 的正弦干扰信号,两个信号在时域上的混合信号为
的正弦干扰信号,两个信号在时域上的混合信号为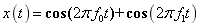 。现以采样率
。现以采样率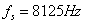 对混合信号进行采样,得到
对混合信号进行采样,得到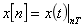 ,
,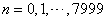
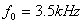 的正弦信号。要求对
的正弦信号。要求对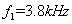 的正弦信号具有不低于
的正弦信号具有不低于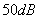 的抑制。将
的抑制。将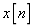 通过该滤波器获得输出
通过该滤波器获得输出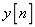 。
。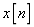 和
和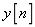 的声音。
的声音。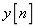 (考虑延迟)与原始信号
(考虑延迟)与原始信号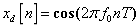 的误差。
的误差。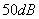 。
。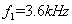 、
、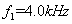 ,重复上述过程,并分析滤波器长度的变化规律。
,重复上述过程,并分析滤波器长度的变化规律。