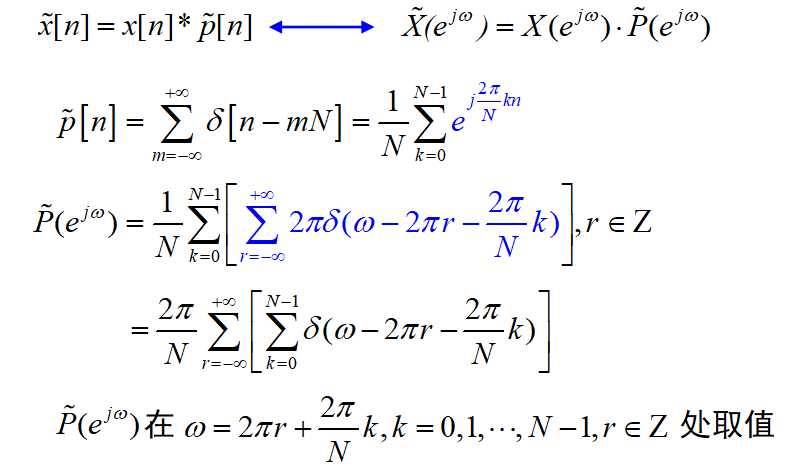数字信号处理总结（持续更新）
离散时间信号与系统
常用典型信号及其表示
连续复指数信号（连续正余弦信号）：
e^jΩt^ = cos(Ωt) + jsin(Ωt)
四个参数：振幅A、相位φ、衰减σ、频率Ω
离散时间正弦序列：
x[n] = A cos( ω0n + Φ )
周期 N：N = 2πm / ω0 为整数
离散时间正弦信号不一定具有周期性
单位阶跃序列
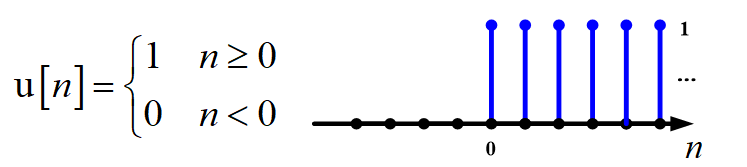
单位脉冲序列
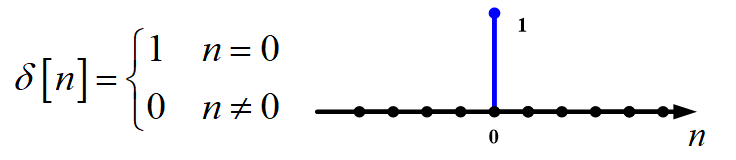
矩形序列
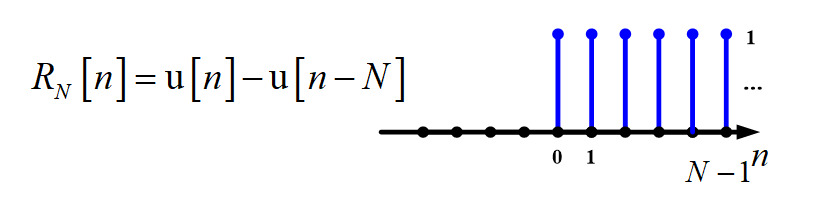
系统属性
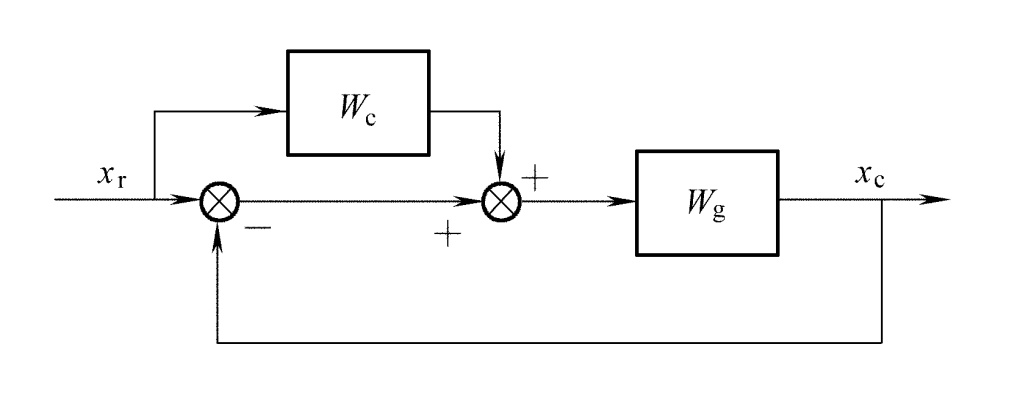
并联、级联、反馈
一般情况下，级联 顺序影响结果
线性时不变系统 跟 级联顺序 无关
LTI系统的卷积和表示
任意序列均可分解成加权延时脉冲线性组合
LTI系统单位脉冲响应及输入、输出间的关系：
交换律、结合律、分配律
N阶后向差分方程：
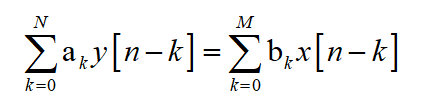
后向差分方程多用于 因果系统 与 数字滤波器 的分析
线性指的是 线性组合 ，并不是因为它对应于一个线性系统，边界条件决定了对应关系
差分方程求解：迭代法（不易求闭合解）、经典法（齐次解和特解）、卷积、Z变换法
差分方程与系统属性的关系：
1、同一个差分方程，不同边界条件，求解结果也不同
2、常系数差分方程不能唯一确定一个系统，给定边界条件才唯一
3、常系数差分方程是构成LTI系统的必要条件
4、零状态的线性常系数差分方程，才相当于线性时不变系统
特征函数及离散时间傅里叶变换
复指数信号是LTI系统的特征函数
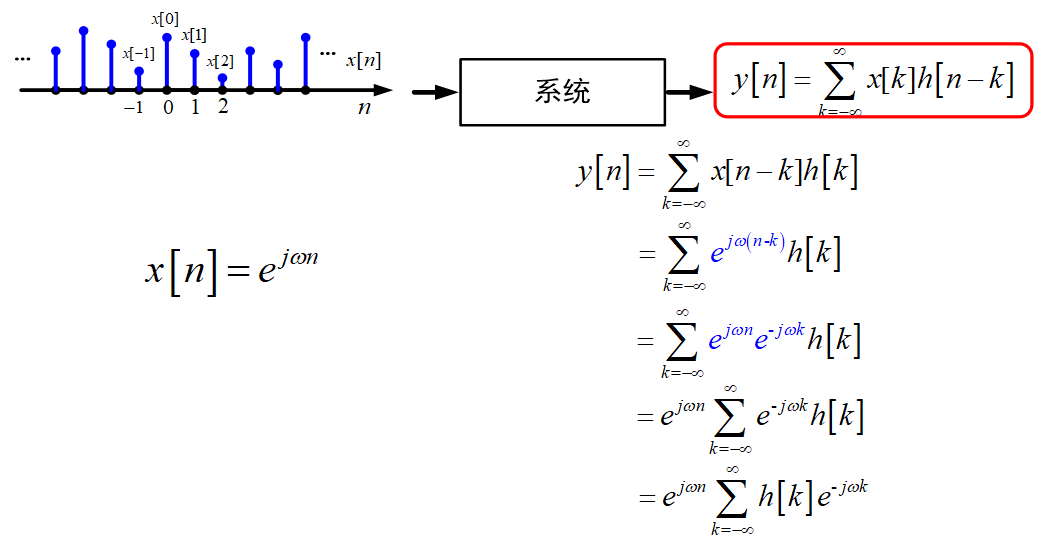
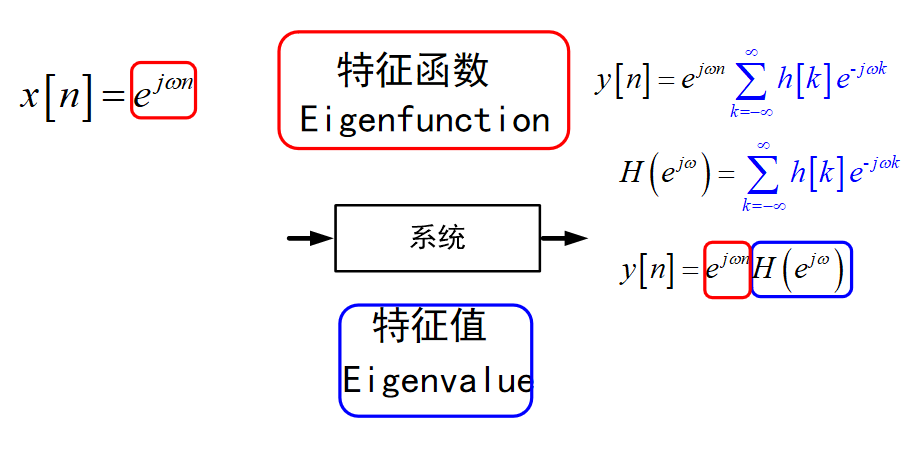
离散时间傅里叶变换（DTFT）
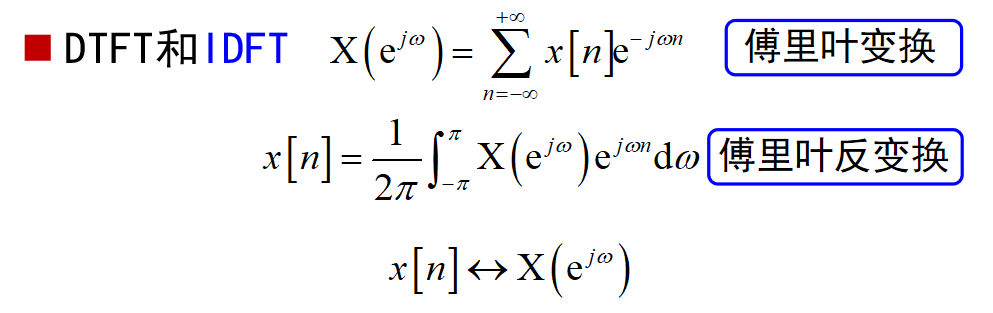
信号DTFT表示的三个条件
收敛条件1：x[n] 绝对可和
收敛条件2：x[n] 平方可和
收敛条件3： 特殊函数 δ(ω)
离散时间傅里叶变换的性质
DTFT的对称性质
1、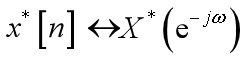
2、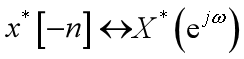
3、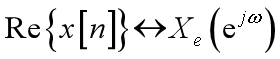
4、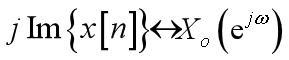
5、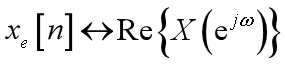
6、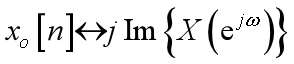
线性、时移、频移、时间反褶
线性：
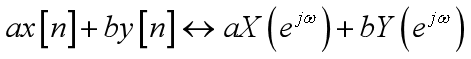
时移：
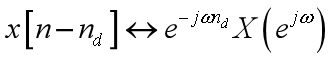
频移：
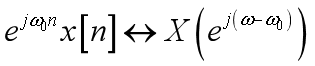
反褶：
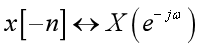
频域微分：
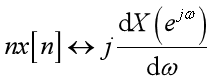
Parsaval定理、时域卷积、调制
帕斯瓦尔定理：
卷积定理：
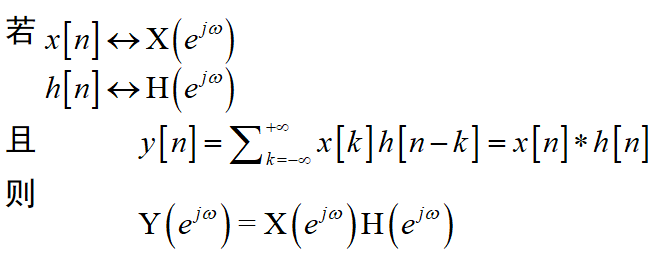
调制：
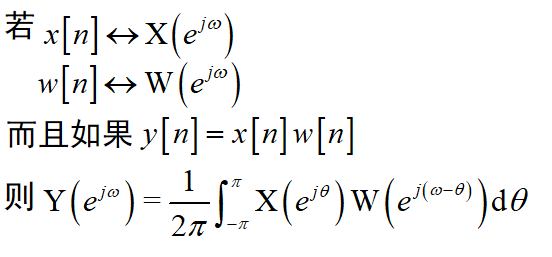
连续时间信号的采样
理想周期采样
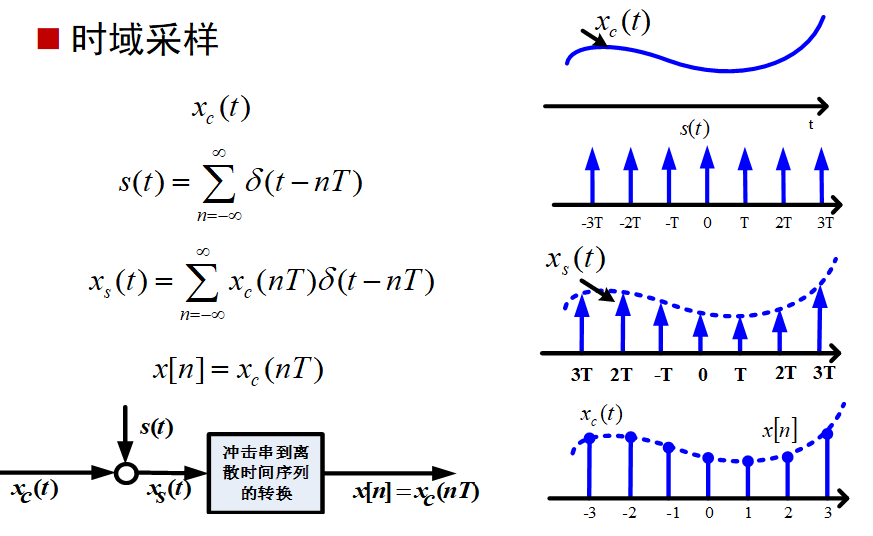
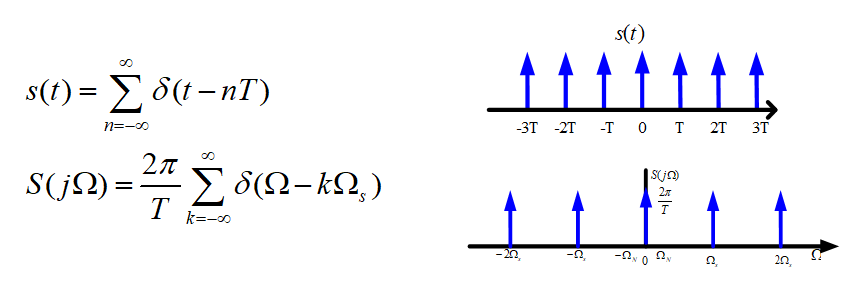
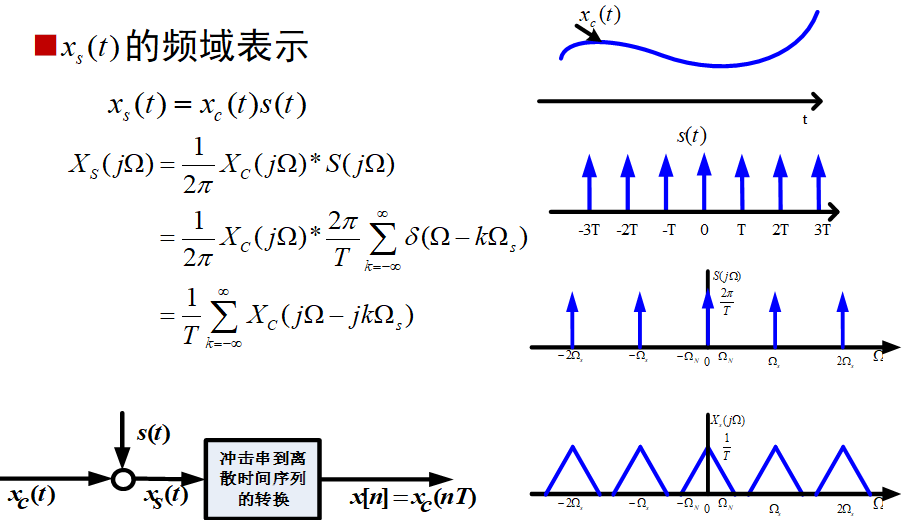
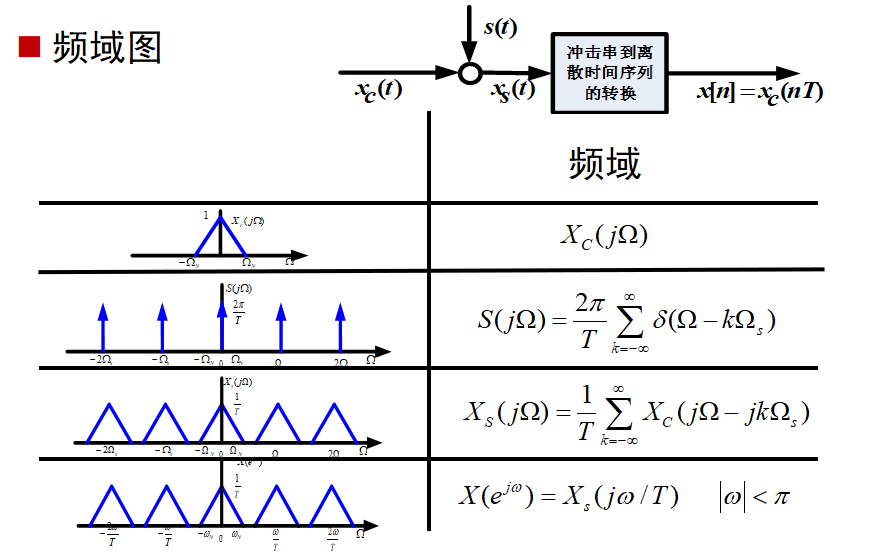
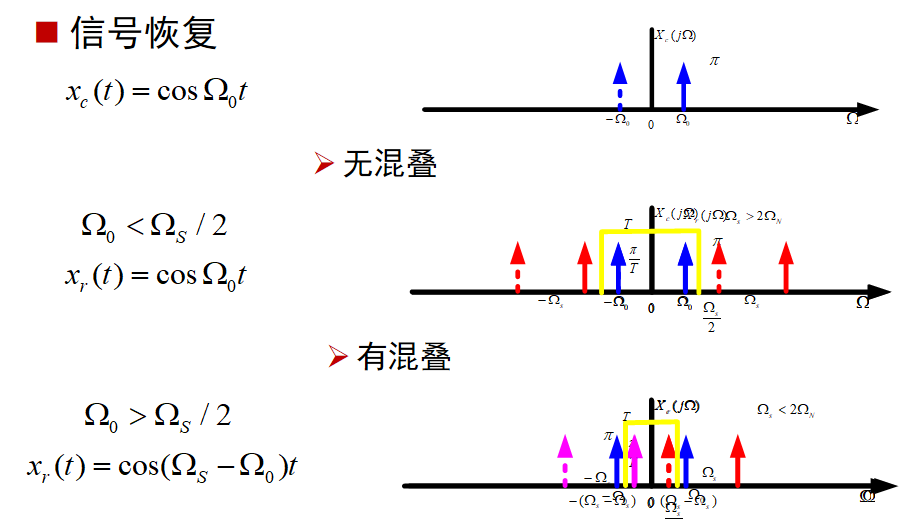
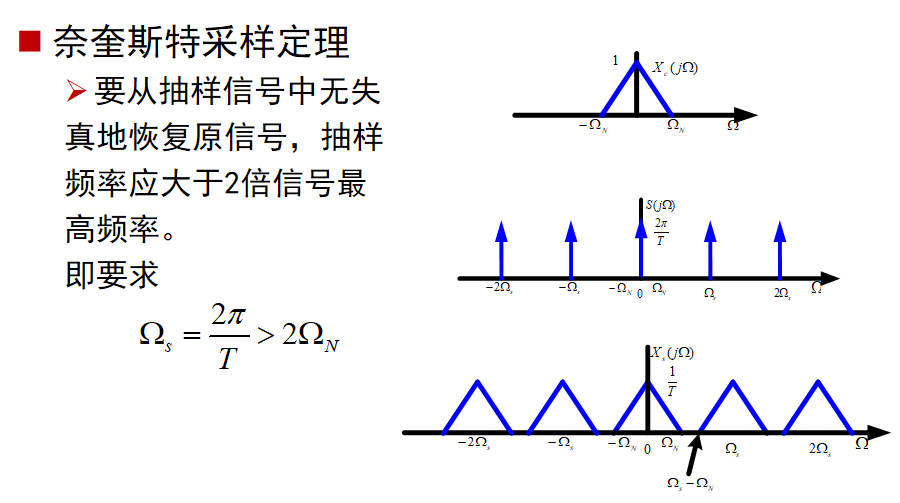
Nyquist采样定理
Z变换
Z变换及其收敛域
双边Z变换：
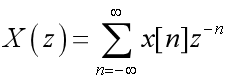
单边Z变换：
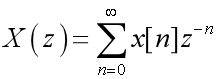
即傅里叶变换是Z变换的特例
收敛域：
1、序列的Z变换不是对所有序列都收敛
2、对给定的序列，使Z变换收敛的那一级Z值称为收敛域，缩写为ROC
3、Z变换收敛条件：
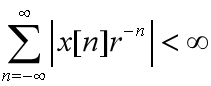
表示方法：
1、级数形式
2、解析表达式（注意只表示收敛域上的函数，同时要注明收敛域）
线性实系数差分方程
由代数基本定理可得出对于实系数差分方程其零点（极点）为实数或者成对出现的共轭复数
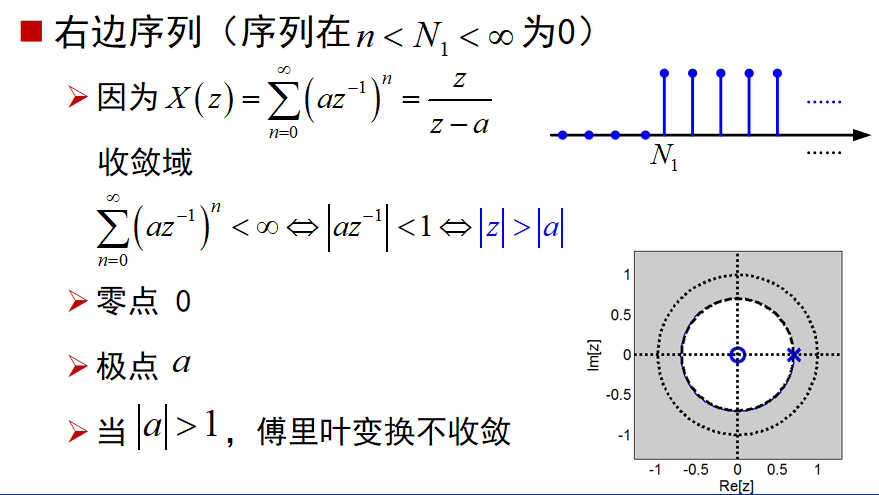
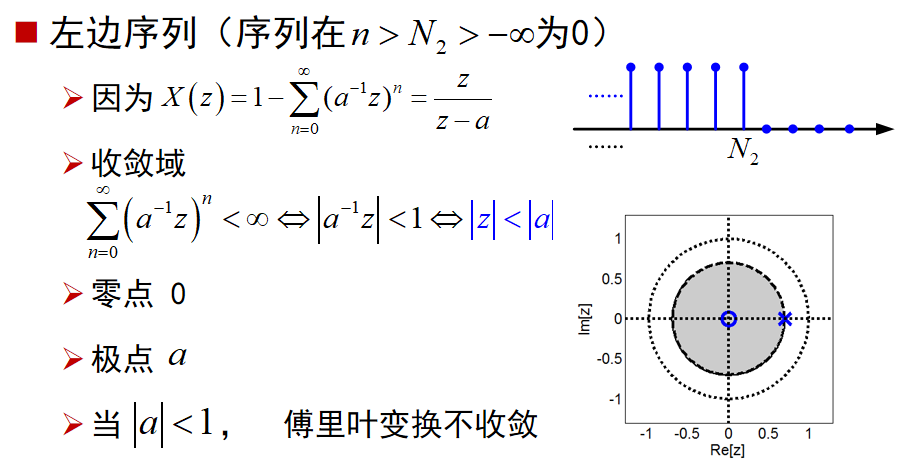
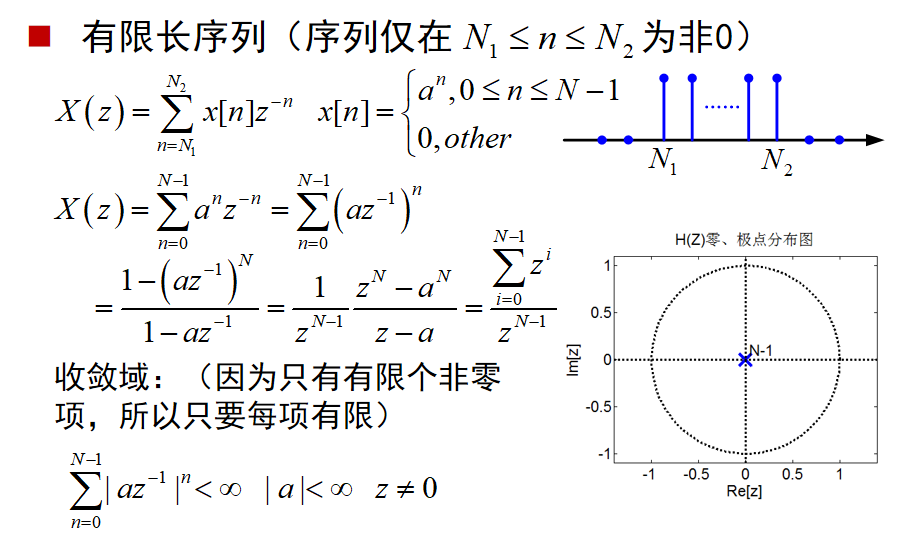
变换域的性质：
1、ROC在Z平面时中心在原点的圆环或圆盘
2、当且仅当 x[n] 的Z变换的 ROC 包括单位圆时，x[n] 的傅里叶变换才绝对收敛
3、ROC不能包括任何极点
4、若 x[n] 是一个有限长序列，其 ROC 就是除 z=0 或 z=∞ 的整个Z平面
5、若 x[n] 是一个右边序列，其 ROC 是从 x[n] 最外面（幅度最大）的有限极点向外延伸至（可能包括） z=∞
6、若 x[n] 是一个左边序列，其ROC是从 x[n] 的 X(z) 的最里面（幅度最小）的有限极点向内延伸至（可能包括） z=0
7、一个 双边序列 可看作一个 左边序列 和一个 右边序列 之和，因此，双边Z变换的收敛域是这两个序列Z变换收敛域的公共部分
8、ROC是一个连通域
系统函数的收敛域与稳定性、因果性的关系
稳定性、因果性和系统函数的ROC
稳定性（当且仅当每一个有界的输入序列都产生一个有界的输出序列，称为BIBO稳定）：
因果性（对每一个选取的 n0 ，输出序列在 n=n0 的值仅仅取决于输入序列在 n<=n0 的值）：
Z反变换及性质
观察法：
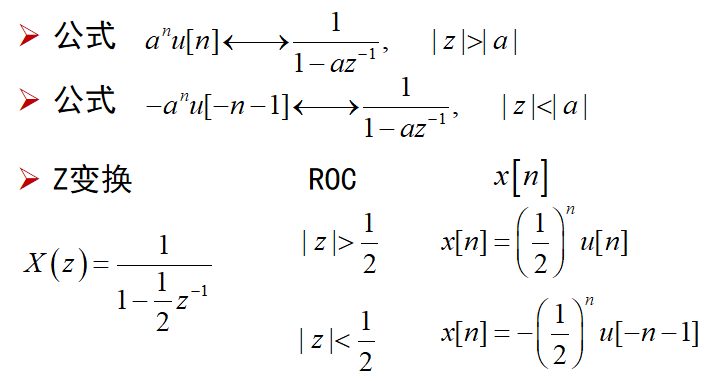
部分分式展开法：
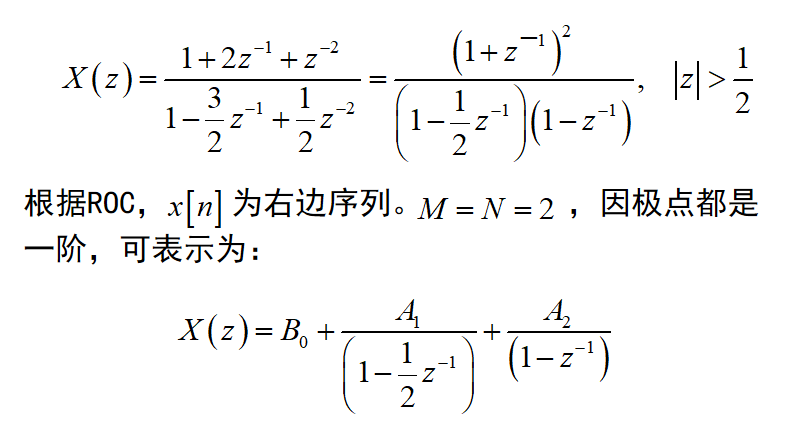
幂级数展开法：
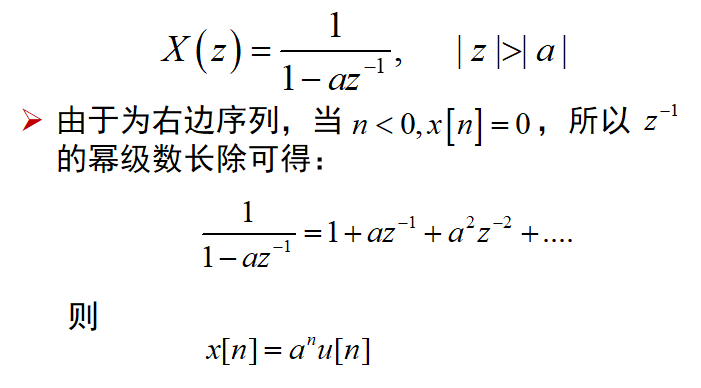
性质：
已知：
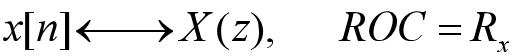
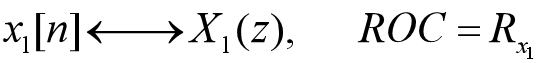
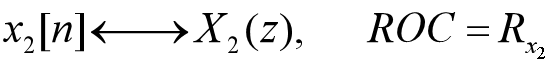
线性：
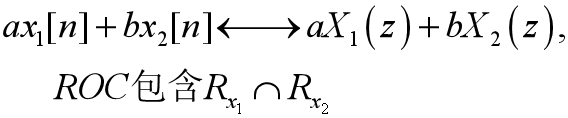
1、组合后序列的极点由 X1(z) 和 X2(z) 的极点组成
2、有可能出现零极点对消，从而扩大收敛域
时移：
微分：
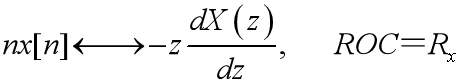
共轭：
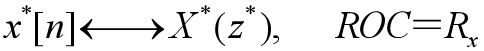
时间倒置：
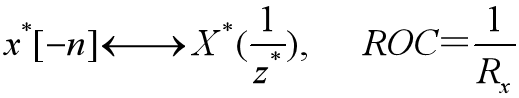
卷积：
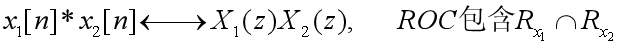
初值定理：
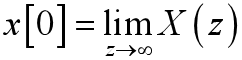
采样的频域表示与恢复
从频域恢复连续时间信号的频谱：
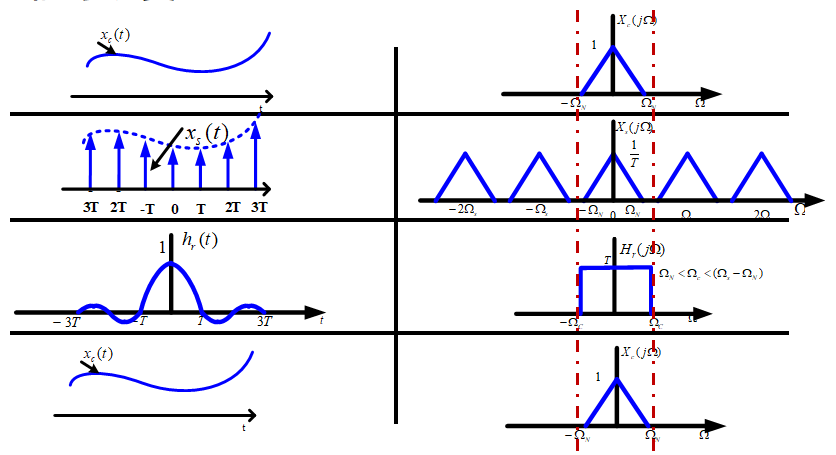
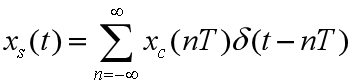
进行傅里叶变换得：
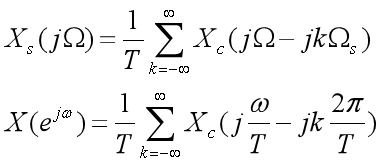
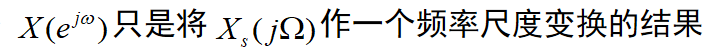：这种尺度变换可以被认为是一种频率轴的归一化，以使得 Ω 中的 Ωs 归一化到 ω=2π
建立连续角频率Ω 、数字角频率ω间尺度变换关系：
ƒ 和 Ω 分别表示 模拟频率 与 模拟角频率 。单位为赫兹（Hz）和弧度/秒（rad/s）,两者关系为：Ω = 2πƒ
ω 单位为弧度（rad）。模拟频率与离散（信号数字）频率之间的关系：ω=ΩT=2πƒ/ƒs **,主值范围 **[0, 2π)
模拟系统非带限时，离散时间处理是对原来的近似，采样频率越大，离散时间系统描述的频谱范围越宽，近似程度也越好
由样本重构带限信号
理想重构滤波器的单位冲激响应
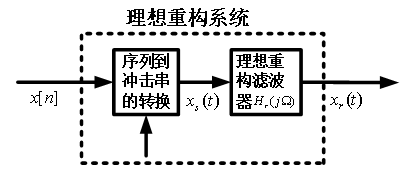
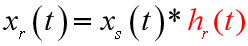
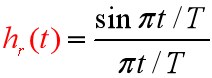
如果不存在混叠，低通滤波器就内插出样本之间的准确值
输入带限信号输出也为带限信号。
低通滤波器的截止频率一般取 Ωs /2 = π / T
离散时间系统设计 - 初步
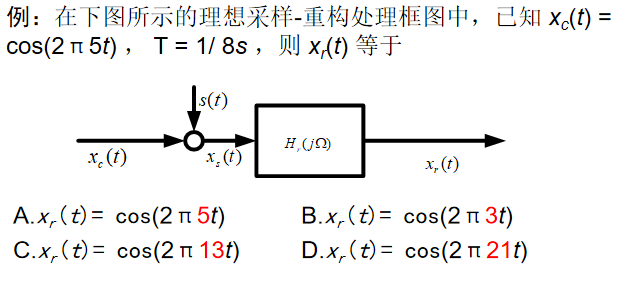
采样前的抗混叠滤波器
离散时间系统的处理流程
采样：
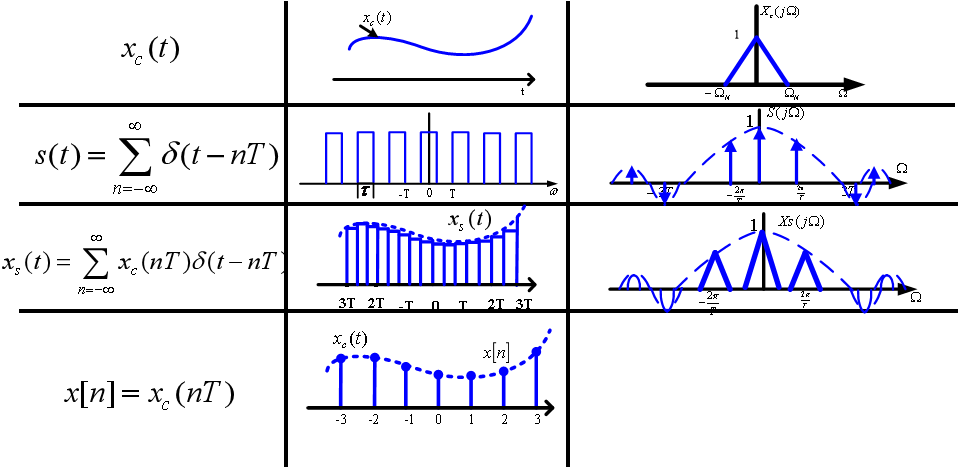
重构：
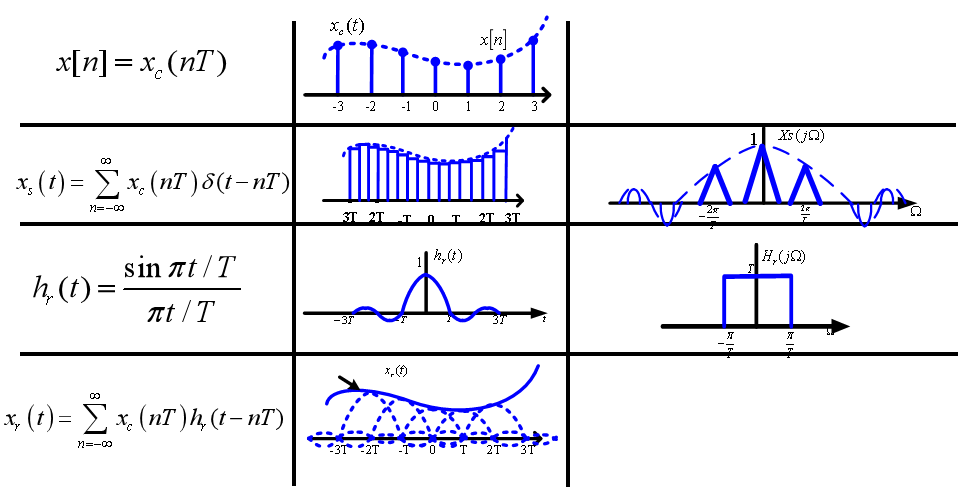
实际处理流程：
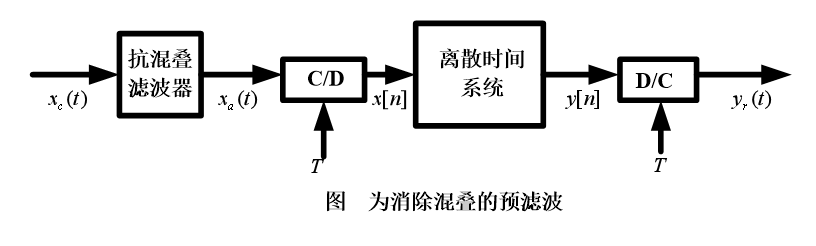
利用离散时间处理改变采样率：
改变采样率可以通过离散信号连续处理（模拟）的方法，也可以利用其离散域的性质在离散域得到。
根据采样率的增减变化可分为：采样率压缩器（压缩器）、采样率扩展器（扩展器）
也可分为：采样率按整数变换、按非整数变换
采样率按整数因子减小：
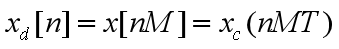
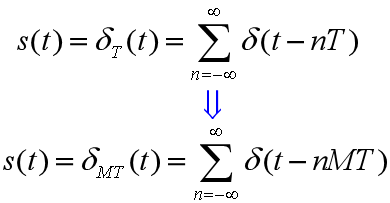
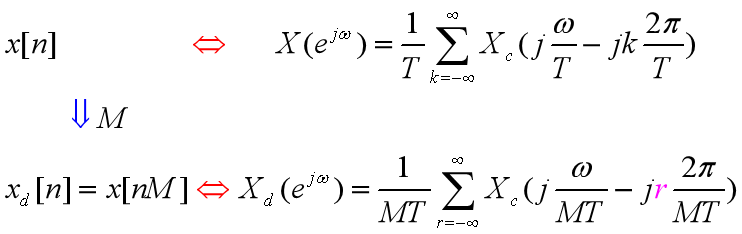
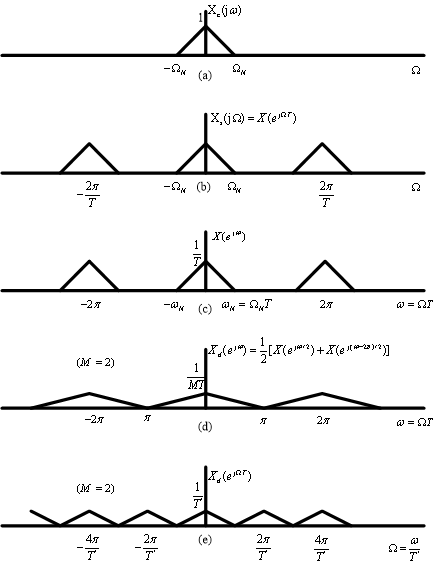
图4.22(d)~(f)具有为避免混叠的预滤波的减采样：
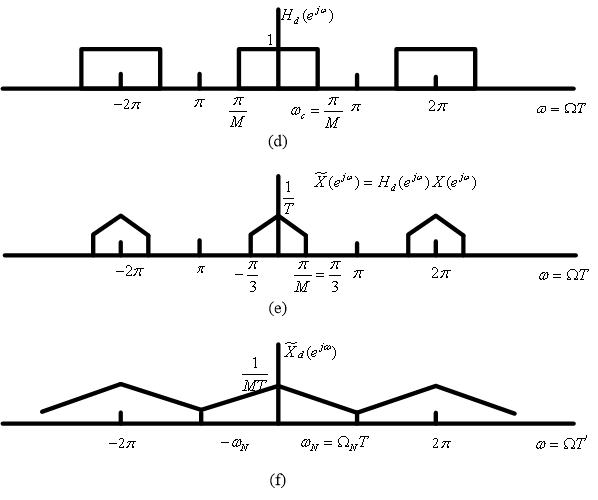
抽取器：
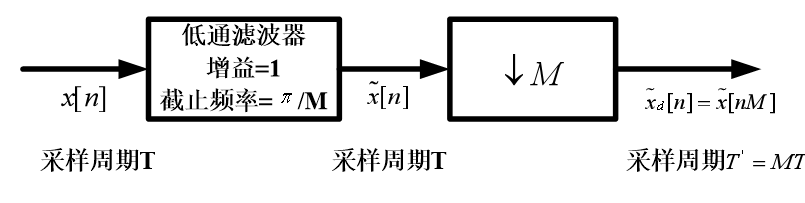
采样率按整数因子增加:
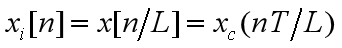
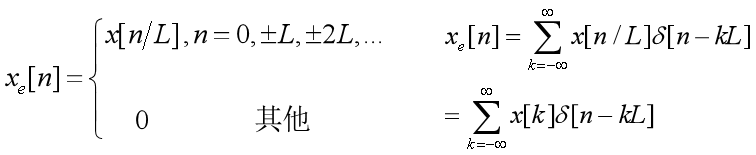
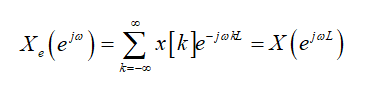
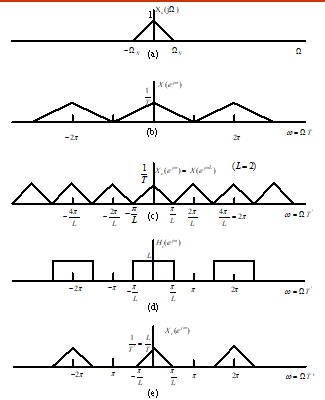
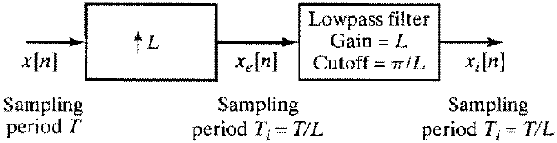
内插器：
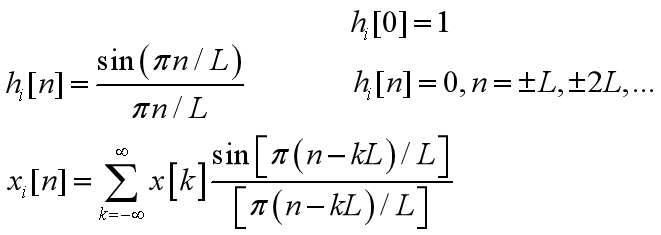
消除混叠的预滤波
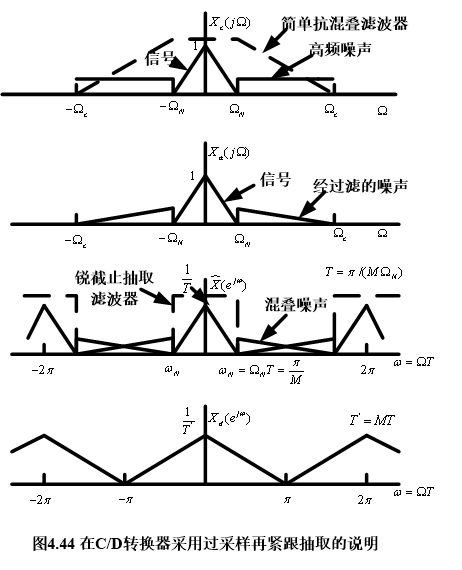
实际：所采样的信号＝有用信号 + 宽带噪声
要求滤波器是锐截至的，单其实现起来比较困难，且成本昂贵，有了数字信号处理技术，可以用简单的滤波器，便可以实现
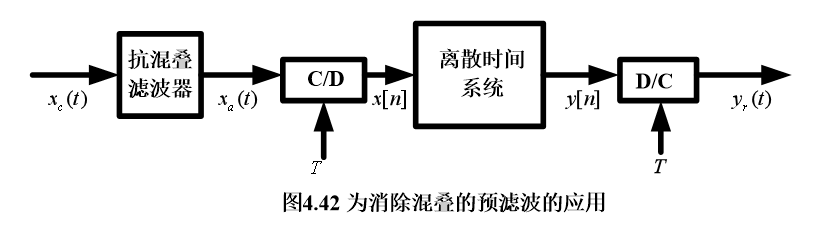
LTI系统的频率响应
选频滤波器的指标（幅度、相位、群延迟）
幅度平方响应：
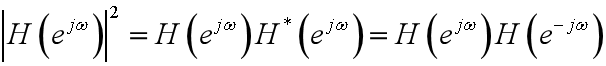
相位响应：
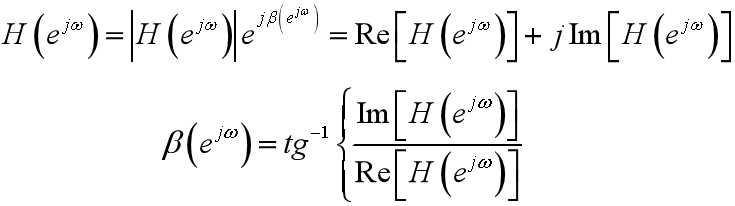
群延迟:
对相位特性线性程度的一种度量，理解成对信号所有频率成分在时域上的延时，线性相位系统的群延时是常数，相当于所有成分都延迟了相同的时间，对信号波形没有产生影响。
群延迟可以看成是由各种频率的波叠加构成的一个波包络，群延迟就是包络的延迟，当群延迟为一恒定值时，包络的形状就不会发生变化，无失真；反之，则各个频率的波延迟不同，组成的波包络形状发生变化，造成失真
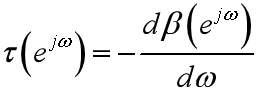
LTI系统的差分方程表示
逆系统、FIR系统、IIR系统
稳定性：
收敛域包含单位圆
因果性：
右边序列（收敛域包含）
逆系统：（零点变成极点，极点变成零点）
若 H(z)Y(z)=1 ，则此二系统互为 逆系统
特点：
系统与其逆系统级联后，总的系统响应为1
逆系统的幅度响应为原来系统的倒数
相位响应和群延迟为原来值的相反数
不是所有的系统都存在逆系统，例：低通滤波器不存在逆系统
最小相位系统：
当且仅当H(z)的零点和极点都在单位圆内时，一个稳定因果的线性时不变系统也有一个稳定因果的逆系统，这样的系统称为最小相位系统
FIR系统：
h[n] 是有限长的（只有前面的有限个累加项），没有非零极点
IIR系统：
h[n] 是无限长的，有非零极点
几何法确定单个零点提供的频率响应
对相位响应而言，零点因式提供的是加号，极点因式提供的是减号
(a)某一系统函数在单位圆上求值的连续相位曲线
(b)相位曲线的主值
(c)为得到 arg[H(e^jw^)] ，需要在 ARG[H(e^jw^)] 上加的 2π 倍数
群延迟的算法：
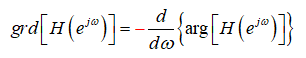
幅度响应与相位响应之间的关系
幅度响应与相位响应之间的关系
任何给定的系统总有一个另一个系统的幅度响应与之相同，但相频响应不同
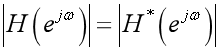
幅度平方可表示为：
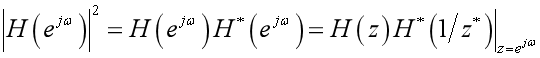
全通系统的零极点分布、相位响应、群延迟特性
当系统的幅频响应满足下式时，为全通系统：
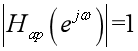
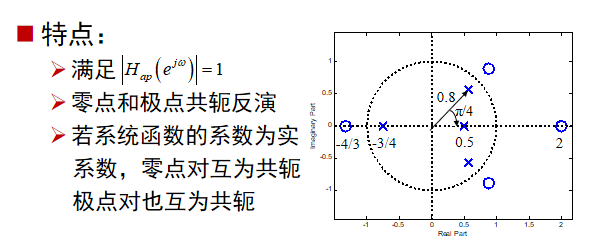
每一个极点都有一个与之配对的共轭倒数零点。
作用：
①延迟均衡器，补偿相位失真
②幅度失真
最小相位系统
定义：
当且仅当 H(z) 的零点和极点都在单位圆内时，一个稳定因果的线性时不变系统也有一个稳定因果的逆系统，这样的系统称为最小相位系统。
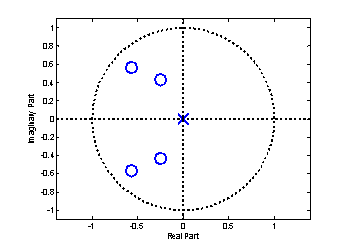
最小相位与全通分解
任何有理系统函数都可写成：
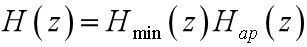
其中包含最小相位系统和全通系统
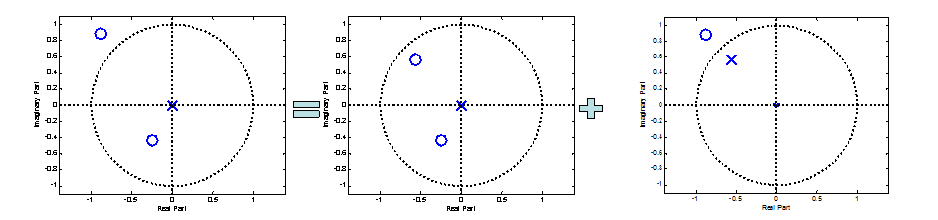
有理系统函数H(z)因式分解，分离出相应的单位圆外的零点，该零点被一个全通系统所吸收。全通系统为原系统提供一个单位圆内的零点，该零点也是全通系统的极点
最小相位的应用及线性相位的引入
最小相位、全通分解 → 频率响应的补偿
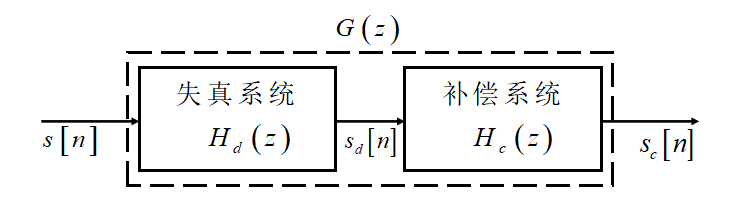
若能实现完全补偿，那么 sc[n] = s[n] ，即 Hd(z) 与 Hc(z) 互为逆系统
若失真系统是稳定、因果的，并且要求补偿系统也是稳定、因果的，那么只有当 Hd(z) 是最小相位系统，且有一个稳定、因果的逆系统，才能完全补偿
eg：
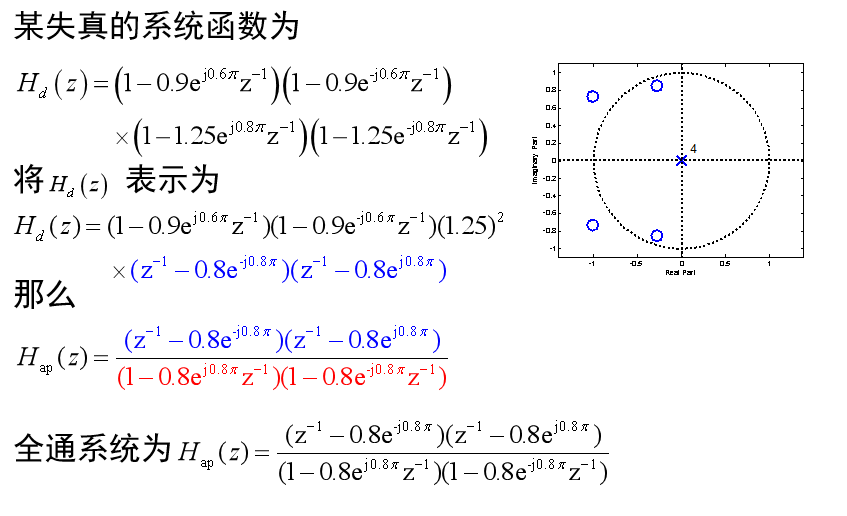
最小相位系统（相位滞后、能量滞后、群延迟）
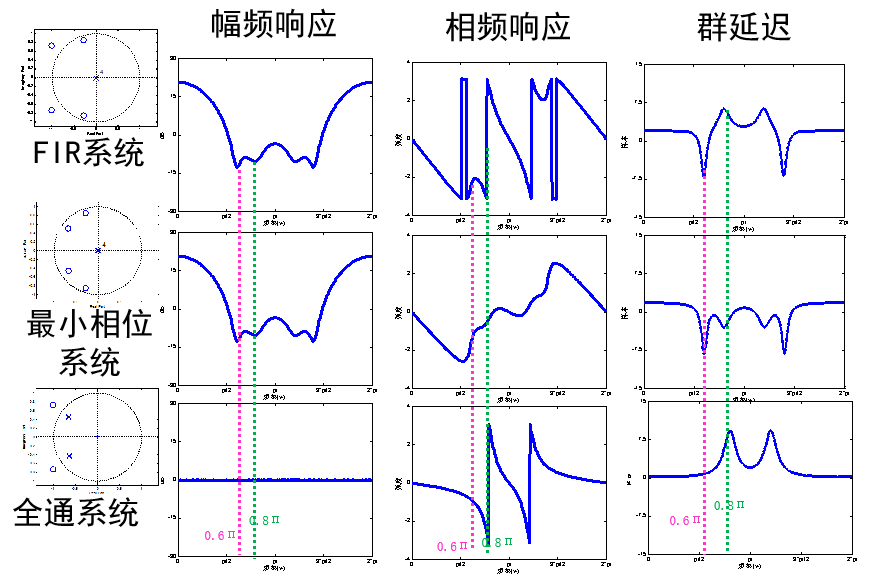
线性相位系统h[n]对称性的引入
当 a 为整数时，单位脉冲响应对 n=a 是对称的，否则不对称
四类因果广义线性相位系统
广义线性相位系统的 h[n] 需满足的条件
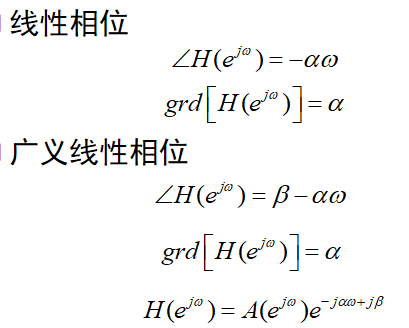
尽管 h[n] 关于M/2对称是广义线性相位的充分条件
具有 有理系统函数 的因果系统，要使它具有 线性相位 ，须为 有限长FIR
四类因果广义线性相位系统
利用广义线性系统关于 M/2 对称，故 n>M 时等于 n<0 ，所以序列长度为 M+1
M分为 偶数和奇数，h[n] 是 奇函数（β=π/2或3π/2） 和 偶函数（β=0或π） 有 四种线性相位
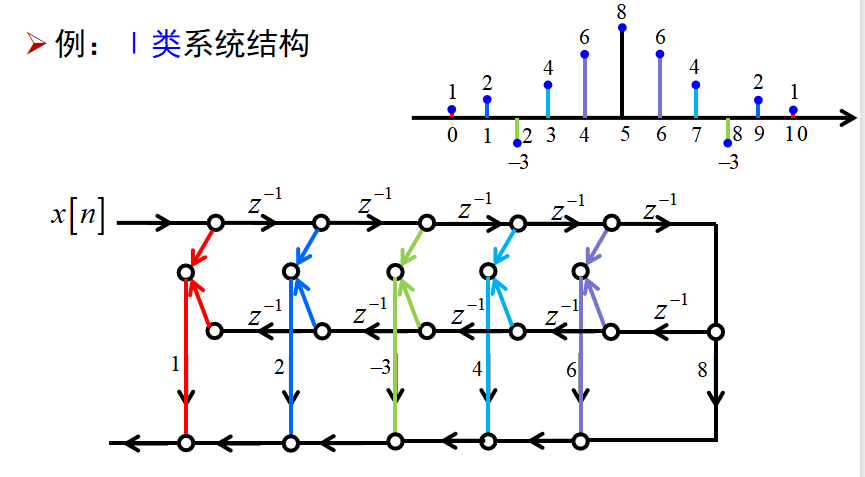
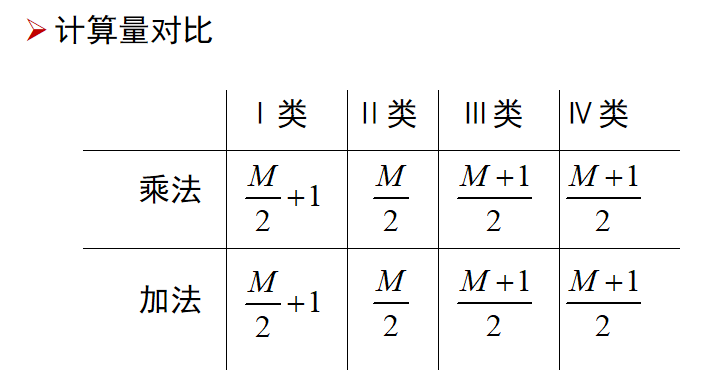
I类FIR线性相位系统：
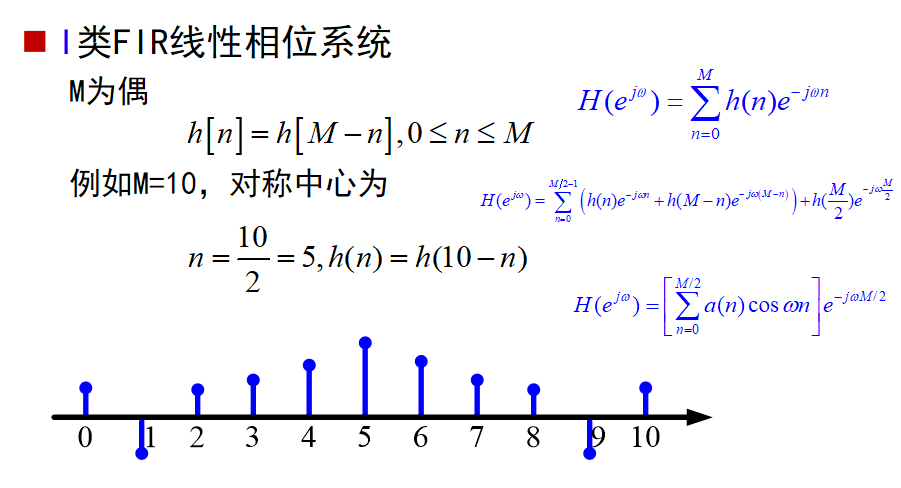
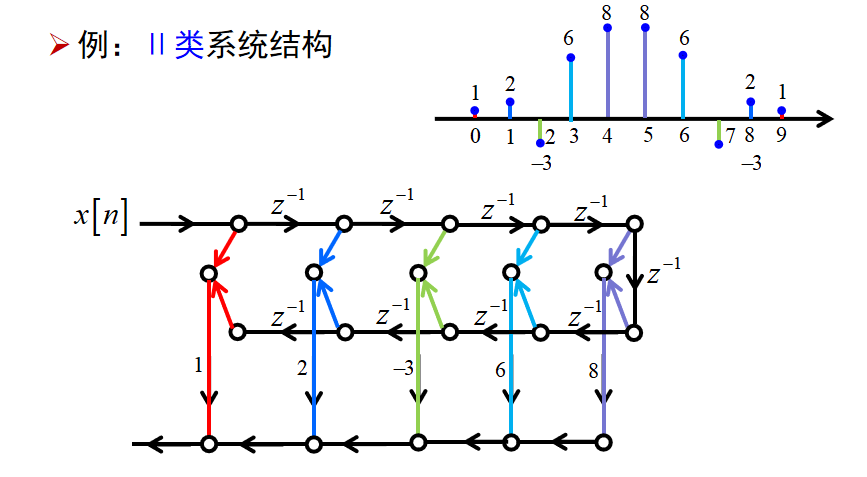
II类FIR线性相位系统：
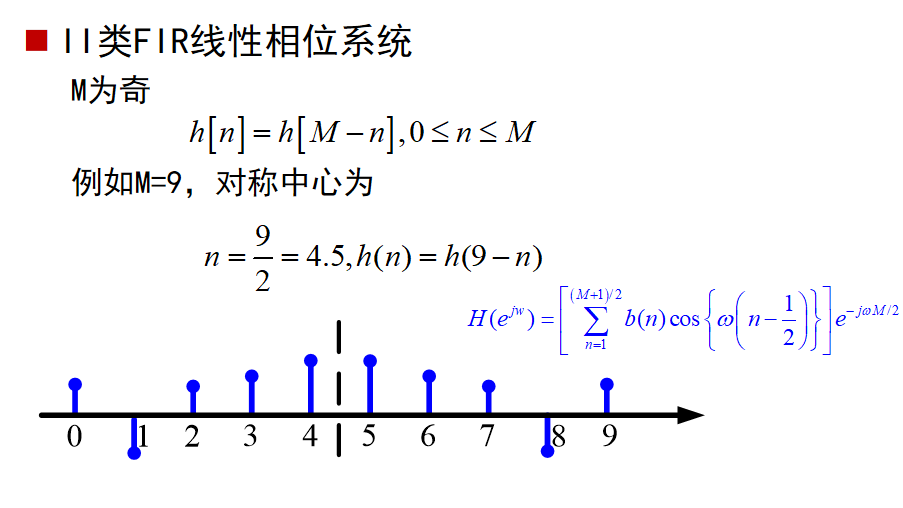
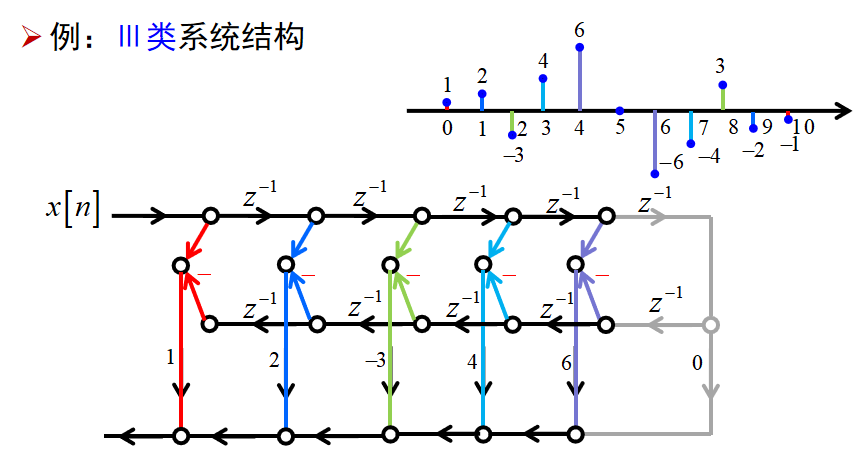
III类FIR线性相位系统：
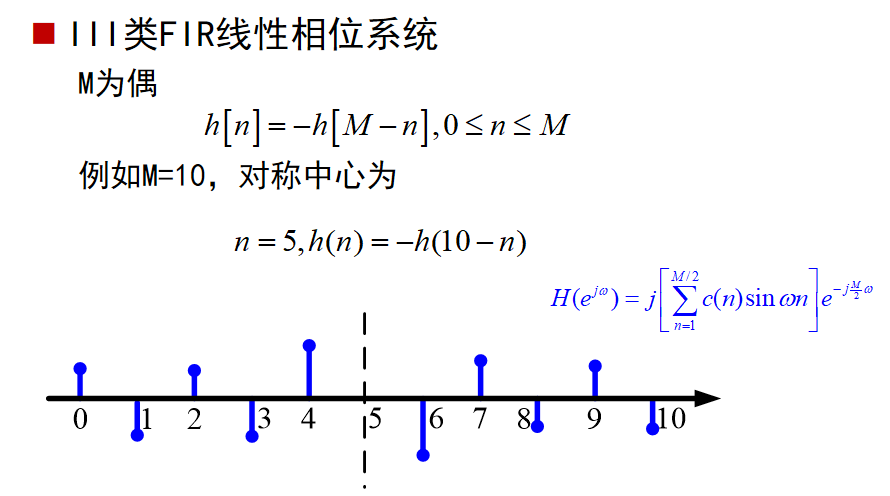
IV类FIR线性相位系统：
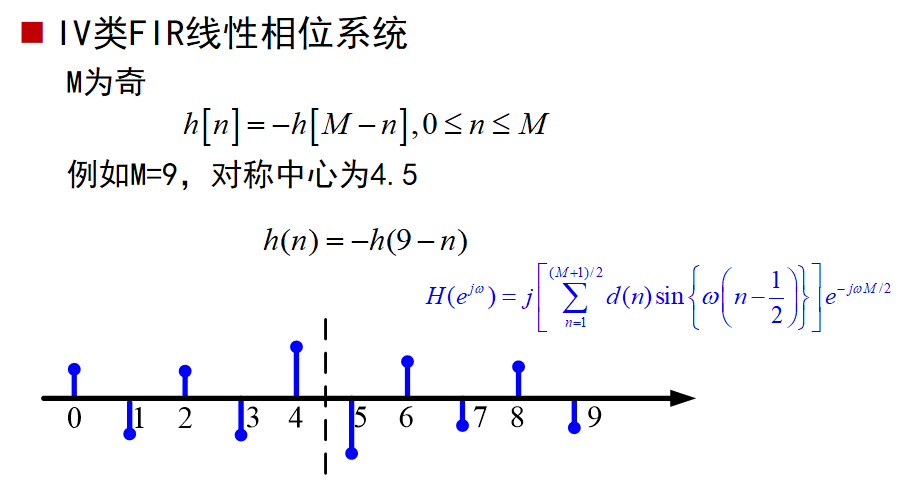
FIR线性相位系统的零点位置
FIR线性相位系统的零点位置
I、II类零点的分布规律：
零点既不在实轴上，也不在单位圆上，则零点是互为共轭倒数的
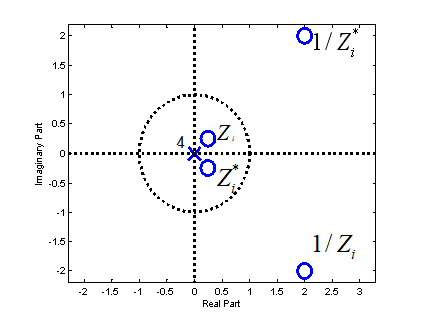
零点不在实轴上，在单位圆上，共轭对的倒数就是他们本身
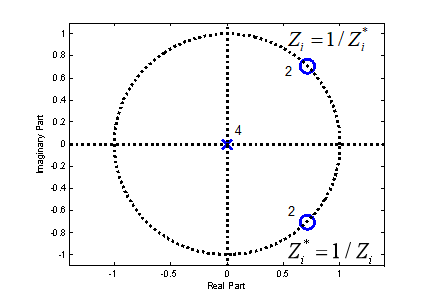
零点在实轴上，不在单位圆上实数零点，没有共轭，只有倒数
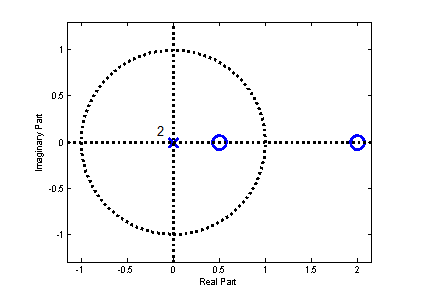
零点既在实轴上，又在单位圆上此时只有一个零点，且有两种可能 ±1
M为偶数，只是恒等式；M为奇数，函数必有一个零点在 z=-1 II类
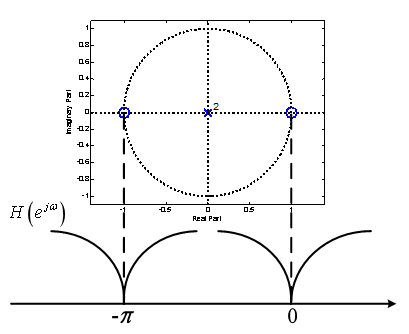
III、IV类系统零点的分布规律：
单位脉冲响应是反对称的：
z=1 时，不论M为奇还是偶，必有 z=1 为零；
z= -1 时，若M-1为奇（M为偶，III类），此时必有 z=1 的零点。
小结：
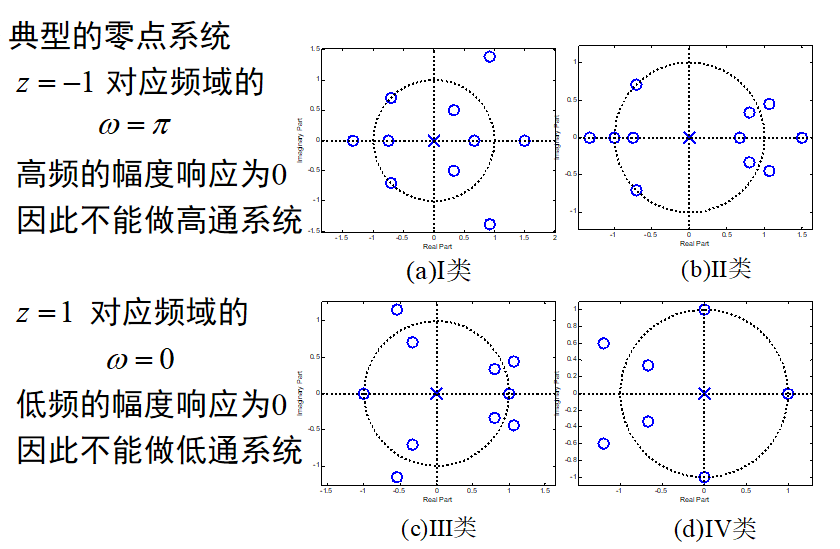
I类应用最广泛，可用于低通、高通、带通和带阻等；
II类不能用于高通、带阻；
III、IV类系数向量奇对称，累加后为0，抑制直流分量；
III类高频时幅频为0，零点还包括 (1+z^-1^) ；
III 、IV类零频处相位π/2 ，用于数字微分器、Hilbert变换器。
IIR系统的结构
直接型、级联型、并联型
离散时间系统结构
FIR滤波器——有限项，可通过卷积实现
IIR滤波器——无穷项，不可通过卷积实现
线性常系数差分方程的方框图表示
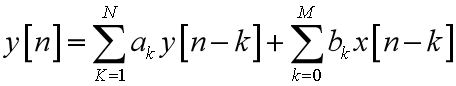
滤波器就是对输入序列 x[n] 进行一定的运算操作，从而得到输出序列 y[n] ，滤波器实现只需3种运算：乘法 、加法 和 单位延迟
乘法次数：N+M+1
加法次数：N+M
延迟次数：N+M
信号流图的基本概：
源节点就是没有流进支路的节点，也称输入节点
汇节点就是仅有流进支路的节点，也称输出节点
分支节点就是一个输入，一个或者一个以上输出的节点
相加节点就是有两个或两个以上输入的节点
第一个网络实现零点，第二个网络实现极点
直接Ⅰ型：
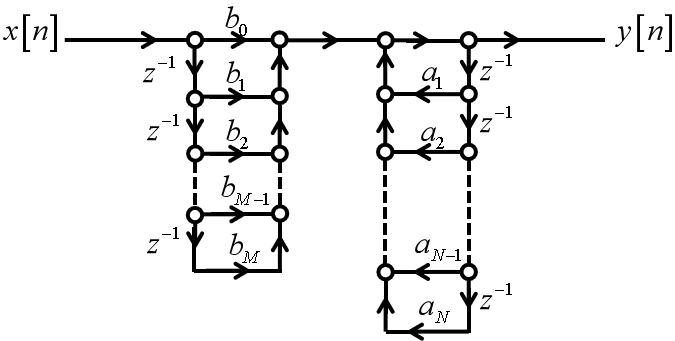
直接Ⅱ型：
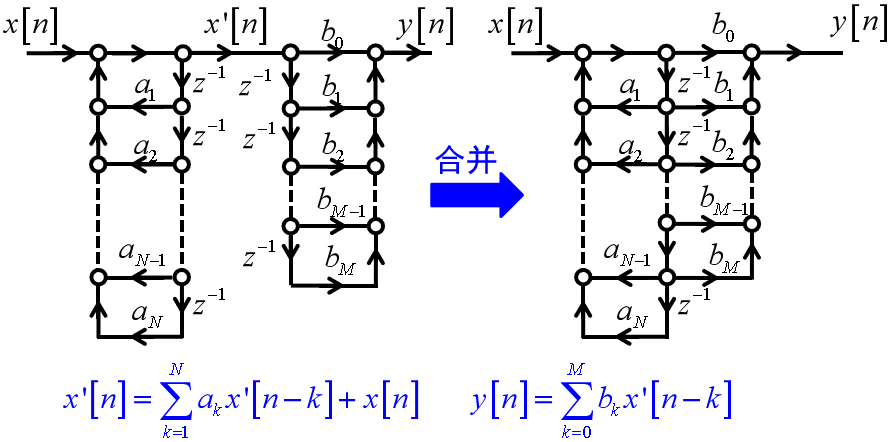
同一种系统有不同的实现方法，其消耗资源的多少不同，我们需要的系统往往是资源和计算量最少的系统。
直接Ⅱ型也称为规范型，其延迟单元最少。
缺点：
①系数对性能的控制作用不明显；
②极点对ak的变化较为敏感。
eg:
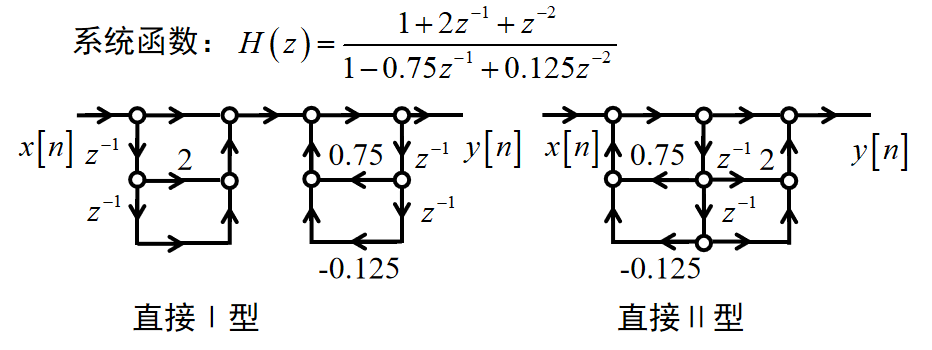
级联型：
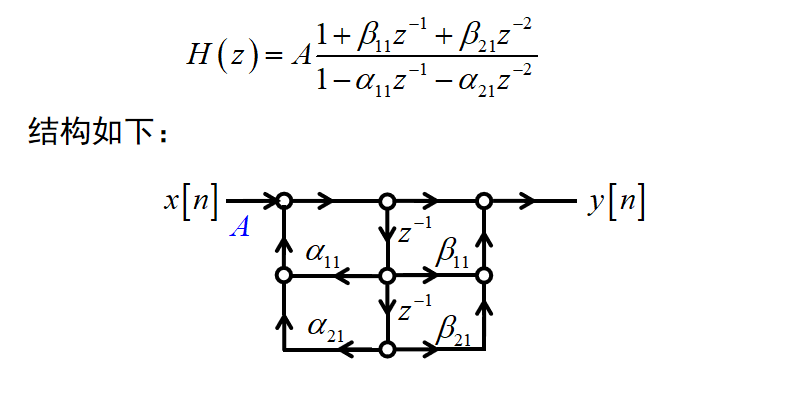
特点：β1k，β2k仅影响第k对零点，α1k，α2k仅影响第k对极点
优点：
①便于调节滤波器特性；
②运算累积误差比直接型小；
③相同结构的子网络结构，可以时分复用。
并联型：
当 M=N 时，将两个一阶实极点合为一项，将共轭极点化成实系数二阶多项式
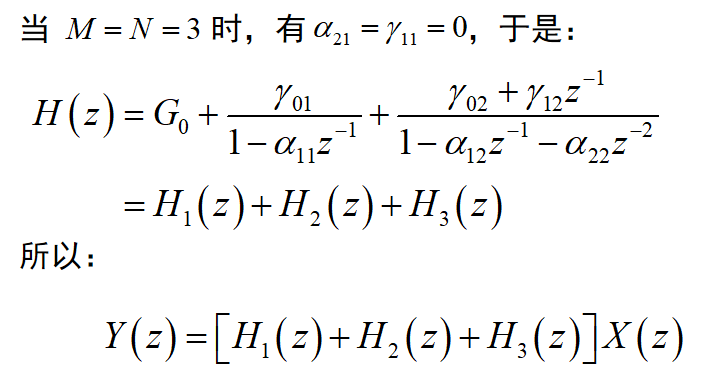
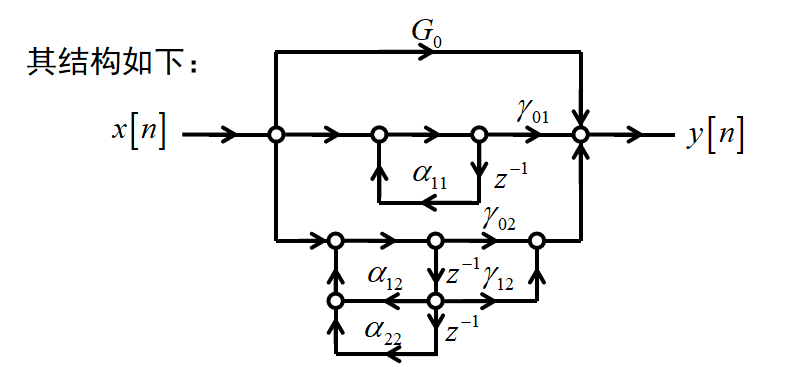
优点：
①调整极点；
②运算累积误差小；
③并联，可同时对输入信号运算，速度最高，多核同步运行
IIR系统的基本结构
IIR系统中的反馈
反馈回路：闭合路径，该路径从某一节点出发，以箭头方向穿过某些支路又回到该节点
IIR系统：存在反馈回路，但不是充分条件
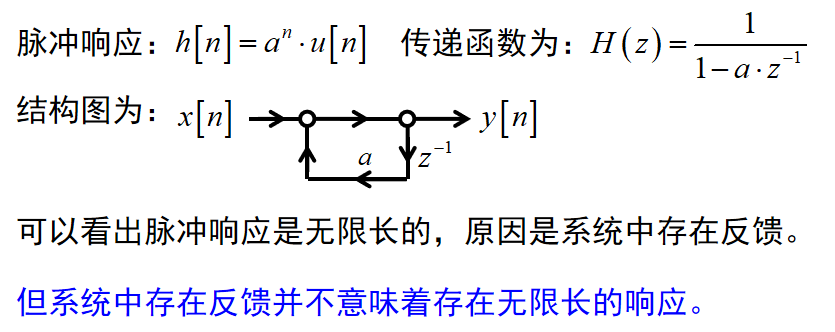
转置型结构、FIR系统的结构
转置型结构
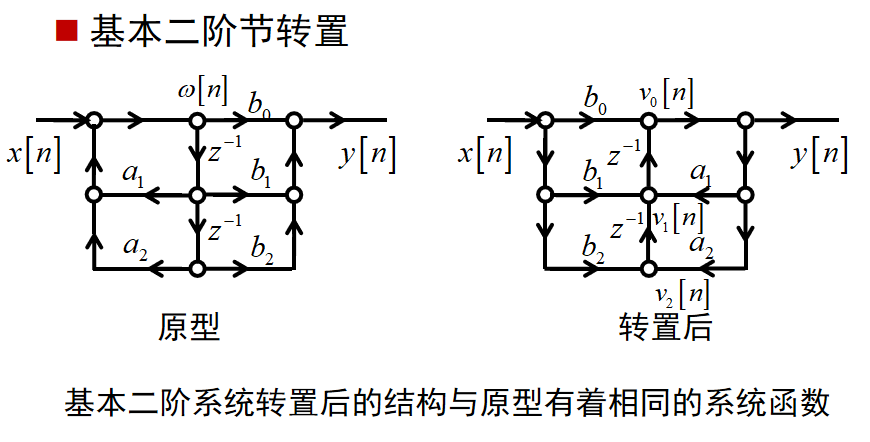
转置前后延迟支路数和系数的个数都不变
直接Ⅱ型结构先实现极点，而转置直接Ⅱ型先实现零点。
在使用有限精度数字实现量化时，存在差别。
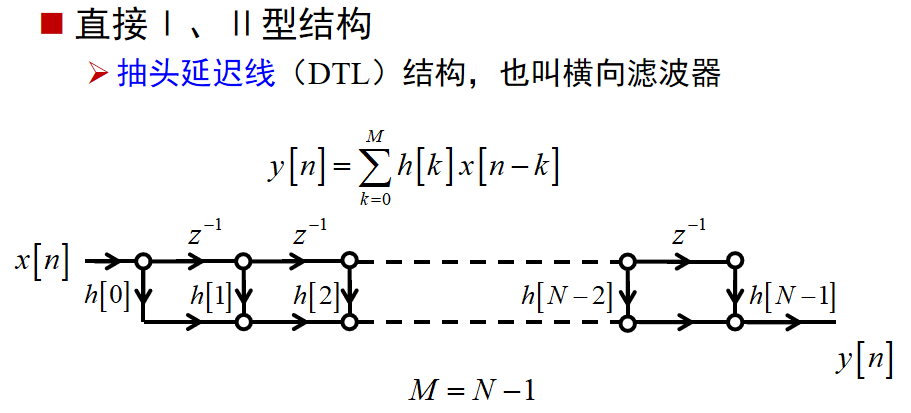
FIR系统的基本结构
直接型：
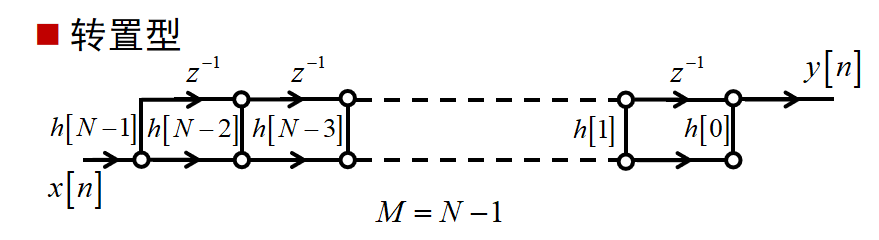
级联型：
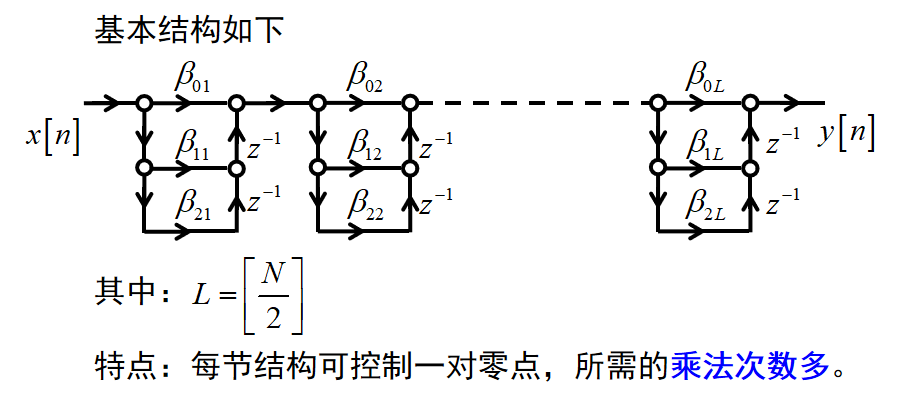
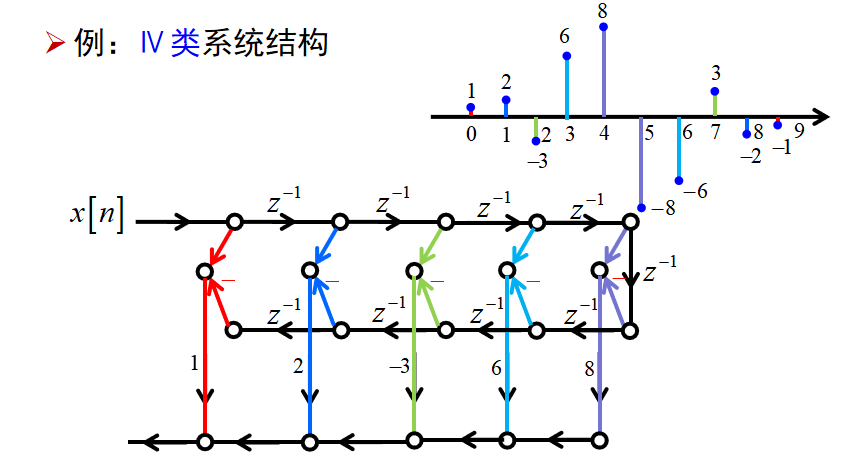
线性相位FIR系统的结构：
对称性可以使乘法器的数目减半
滤波器设计方法
选频滤波器
能让某些频率分量通过，而完全拒绝其他频率分量
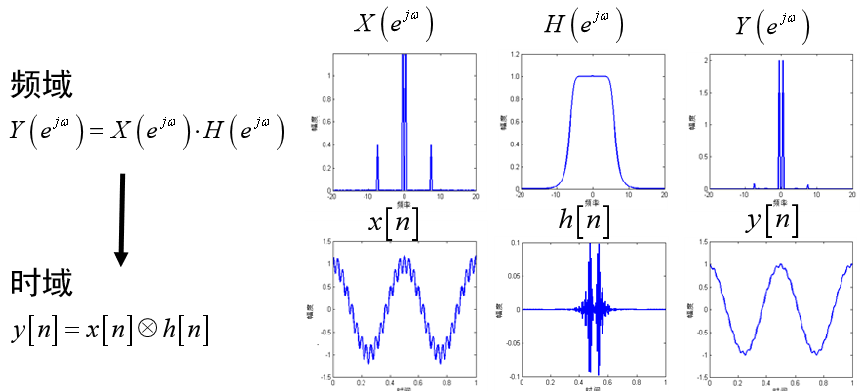
广义滤波器
任何能对频率进行修正的系统(我们需要的是线性时不变的因果系统)
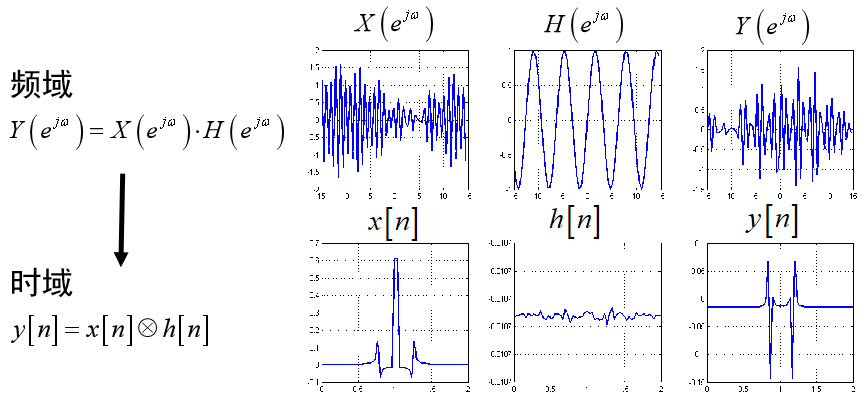
滤波器的设计步骤:
给出系统的性能指标，用因果离散时间系统逼近这些性能指标
频域的形式：低通、带通、高通、带阻
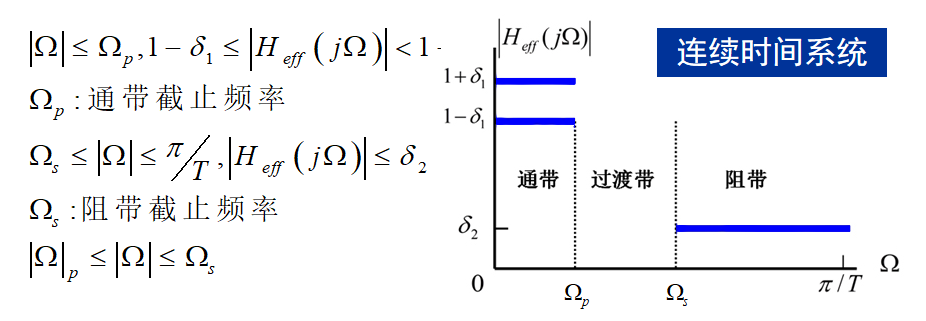
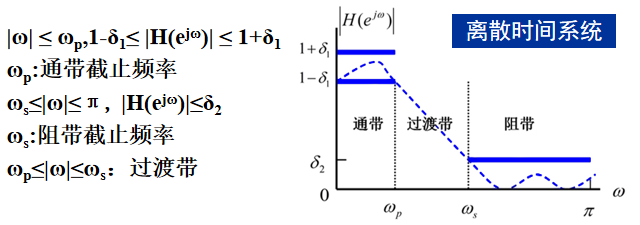
所示LTI连续系统,可通过 ω = ΩT 将有效连续时间滤波器的指标转换为离散时间滤波器的指标
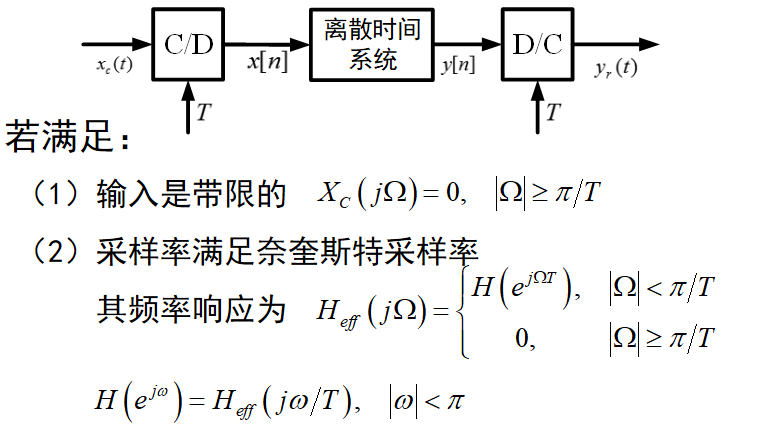
由连续时间滤波器设计离散时间IIR
利用数字计算的方法实现系统，该离散时间滤波器称为数字滤波器。
按照离散系统时域特性，可分为无限冲激响应（IIR） 和 有限冲激响应（FIR）
冲激响应不变法：
乘上Td 是为了在一个周期中与h[n] 的幅度相同；只要采样，就有可能产生频谱混叠
H（s） ？–> H（z） ：z = e^st^
如果有极点是sk ，会被映射到e^skTd^ ，零点不满足这种对应关系
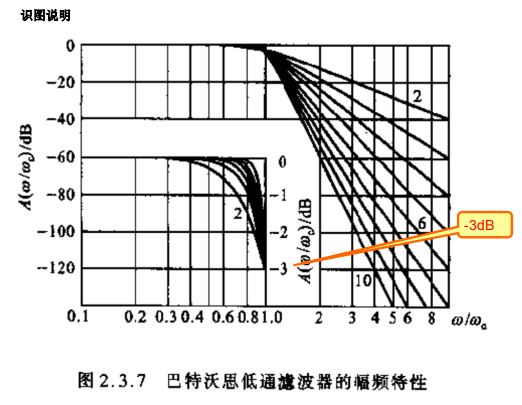
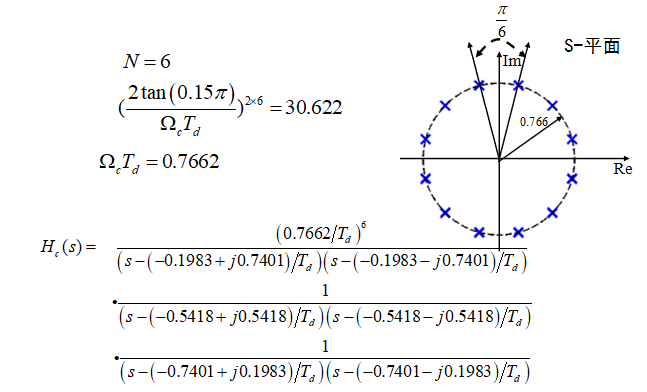
Buttworth滤波器设计及举例
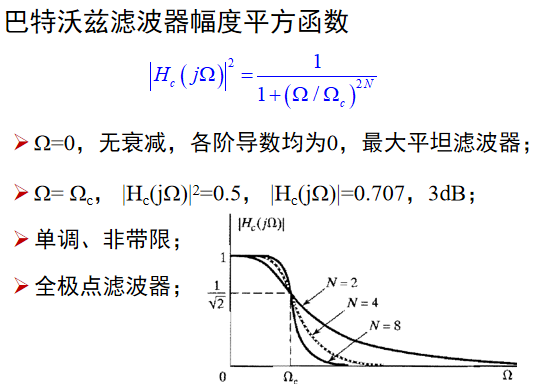
虚轴左面是N各点平分180°，例如N=3，分别为120°、180°、240°
例题：
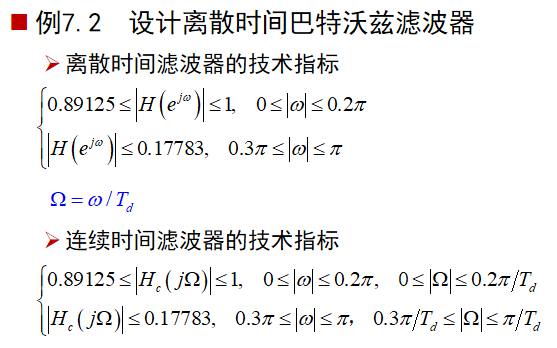
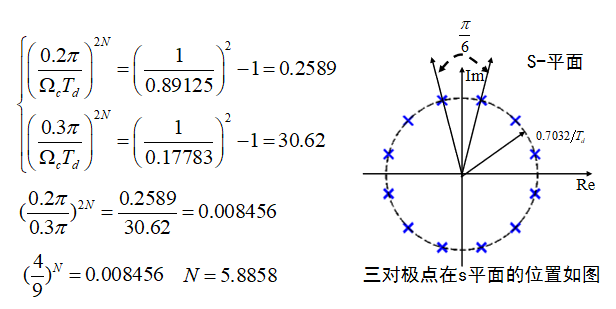
把N = 6代入通带 ！！！可能会混叠，余量给阻带，N尽量大一些
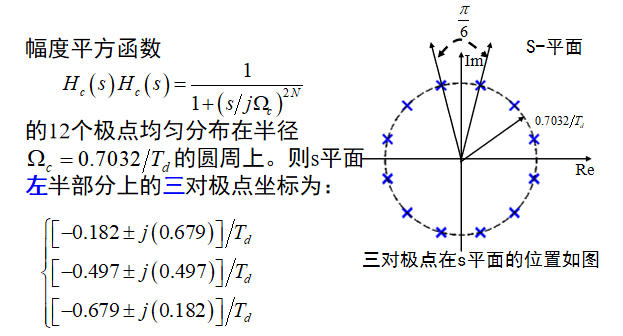
Td 的作用：采样周期 Td 不影响滤波器的设计，不能控制混叠
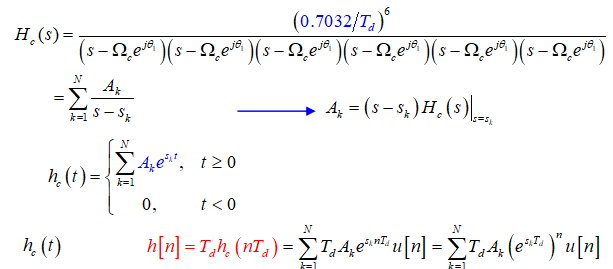
若采样率增加（Td 减小），连续时间系统的截止频率必须成比例的增加
超标设计，尤其是阻带指标
采样周期越小（采样频率越高），混叠越小
除非原来的模拟滤波器带限的，通带截止频率小于 Ωs / 2
如果连续时间滤波器在高频部分趋于零，则混叠就很小，可以忽略。
高通 和带阻 滤波器不满足以上要求，会产生混叠，∴ 该方法不适用
双线性变换法：
重点是找到单点映射
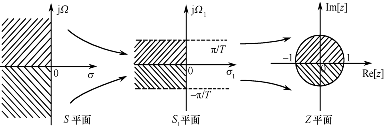
变换公式：
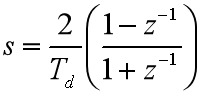
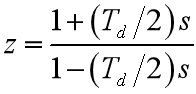
注意收敛域，即s的左半平面和z平面单位圆之间的映射关系
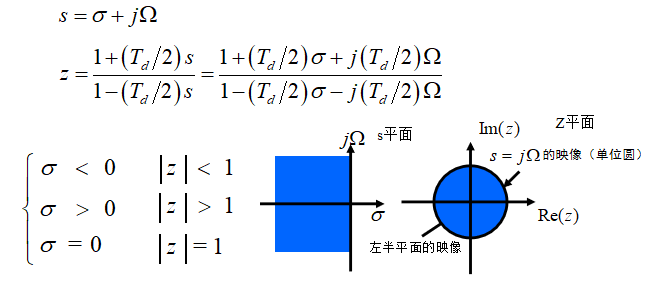
ω 和 Ω 的映射关系：
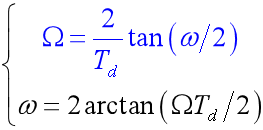
• 避免了混叠
• Ω与ω的非线性关系
• 适于分段常数型的滤波器设计
• 在双线性变换后各个分段边缘的临界频率点将会产生畸变
• 频率预畸变
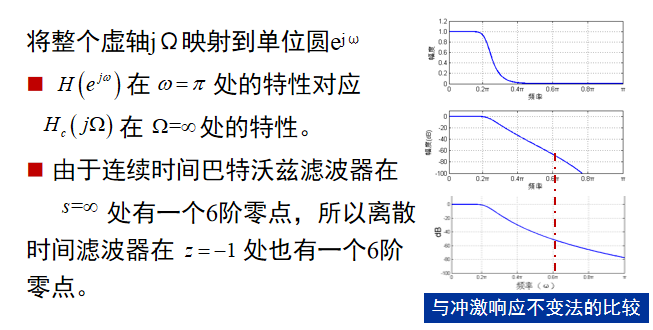
例题：
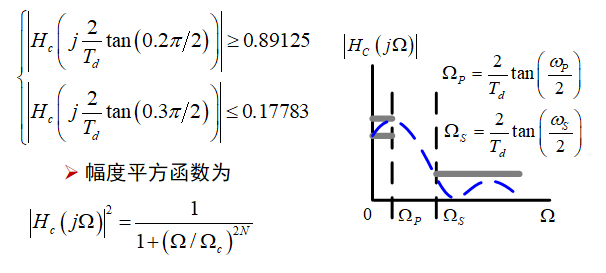
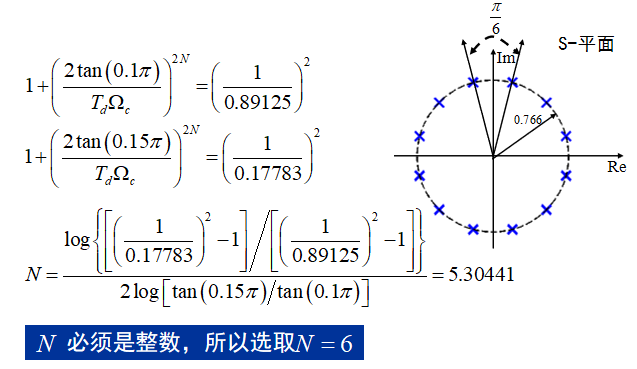
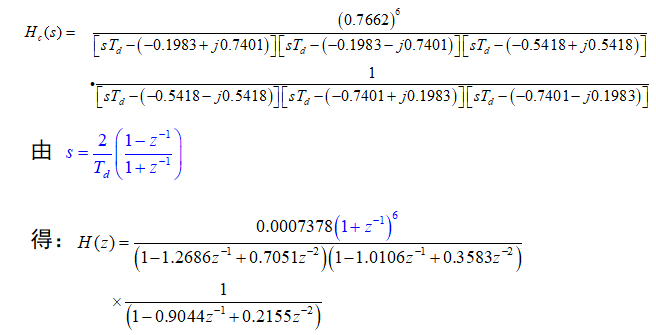
总结：
s域 与 z域 变换关系：
冲激响应不变法：
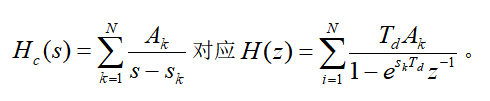
双线性变化法：
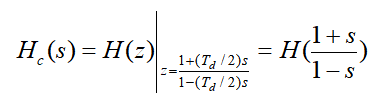
窗函数法设计FIR滤波器
IIR滤波器中有反馈回路，因此量化误差、运算误差迭代累积，增加了不确定因素，如稳定性问题；
FIR滤波器不考虑极点，避免了设计中的频谱因式分解问题，可以设计出严格线性相位；
窗函数法：
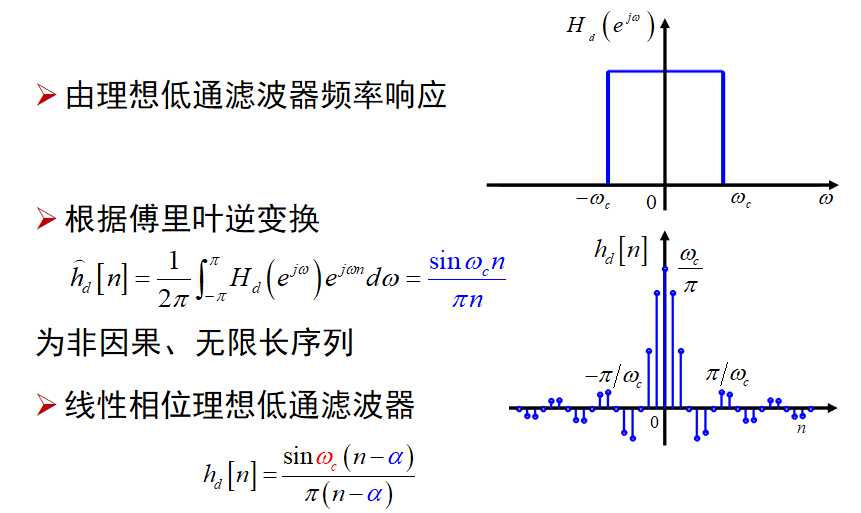
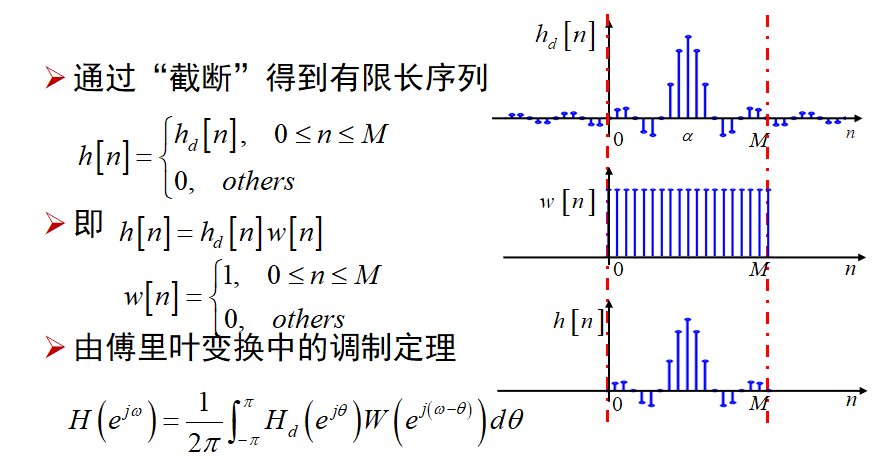
矩形窗的频谱
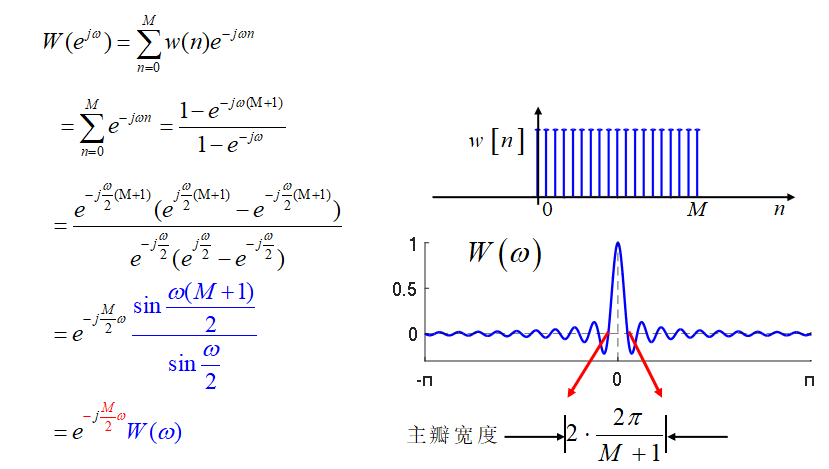
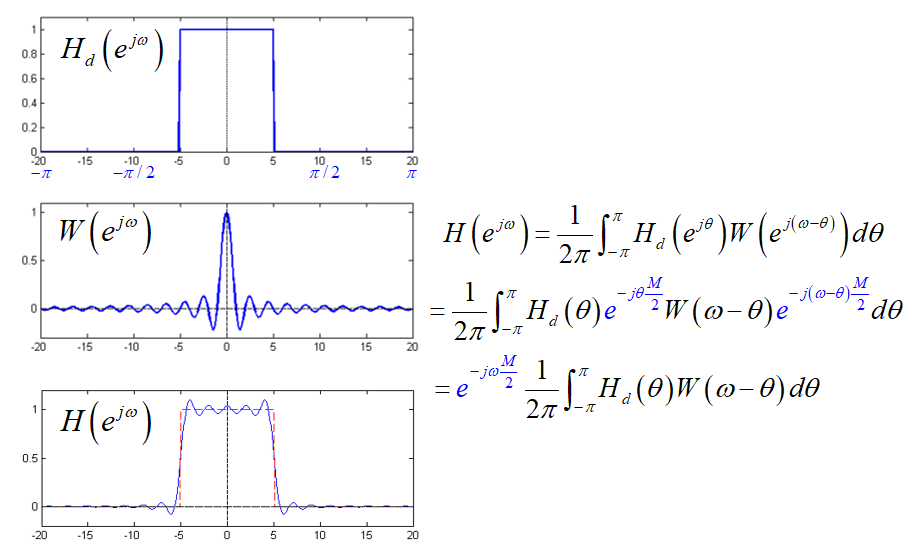
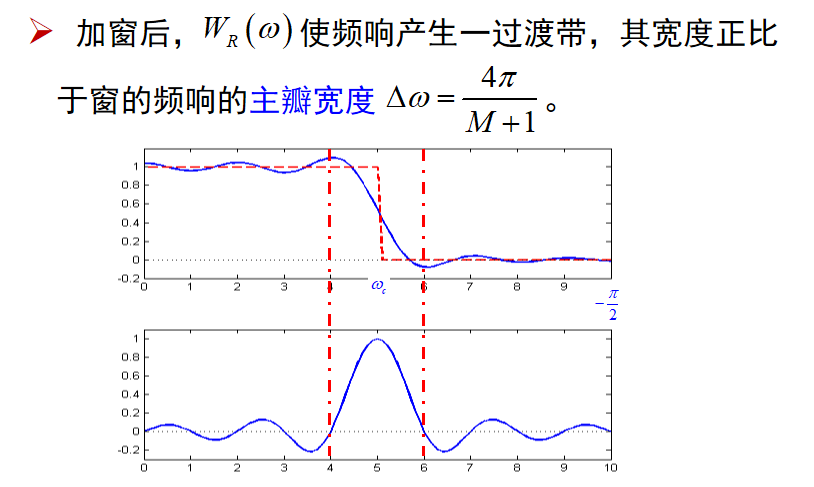
吉布斯(Gibbs)效应
对于矩形窗最大相对肩峰8.95%，不管N怎样改变，最大肩峰总是8.95%，或阻带衰减21dB
FIR滤波器的Kaiser窗设计法
窗谱：窗函数的频响的幅度函数亦称作窗谱。
对窗函数要求：
希望窗谱主瓣尽量窄，以获得较陡的过渡带，这是因为过渡带正比于主瓣宽度。
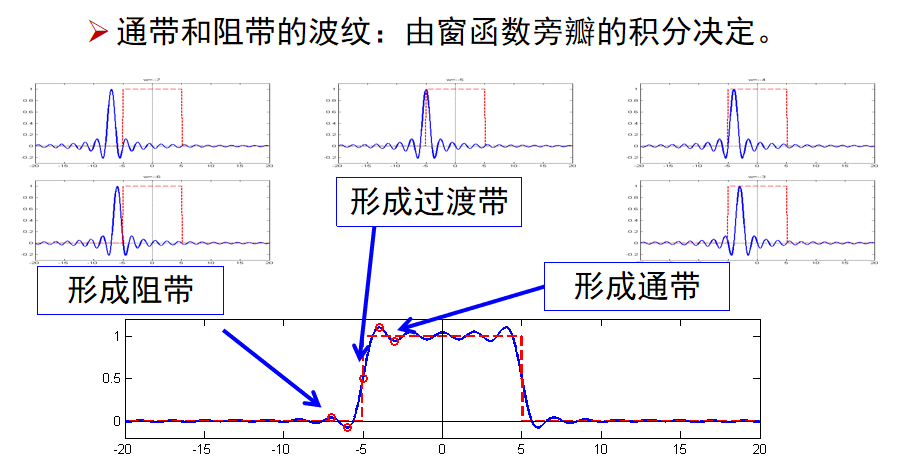
尽量减少窗谱最大旁瓣的相对幅度，这样可使肩峰和波纹减小。
常用窗函数的性质
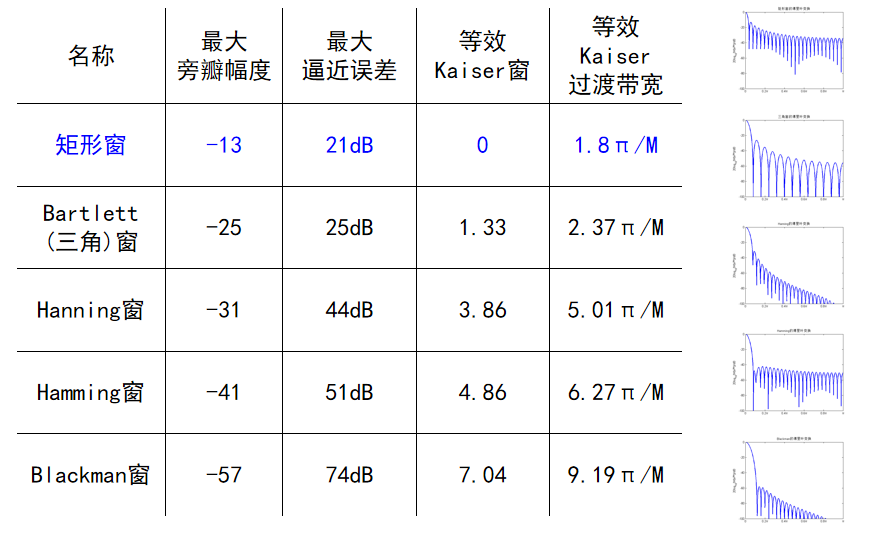
广义线性相位的合并
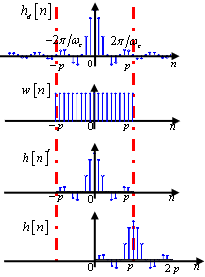
系统为广义线性相位
幅度响应部分就是两个实函数的卷积
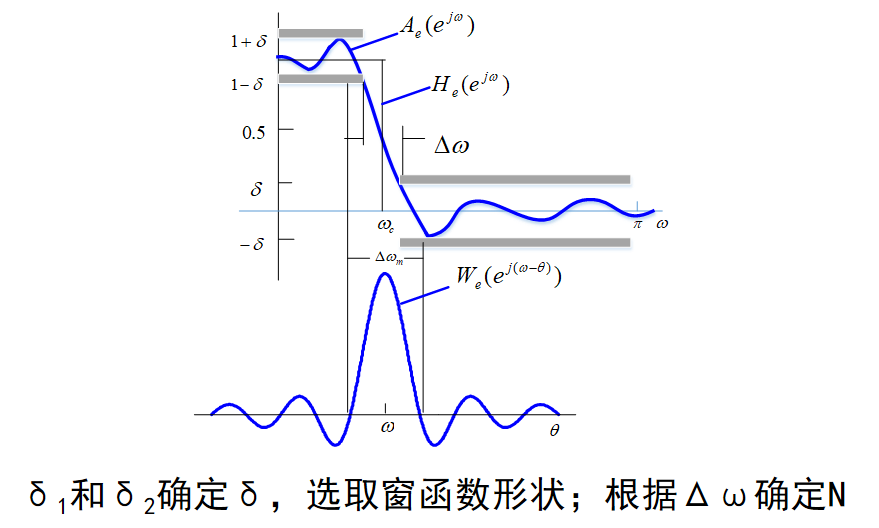
Kaiser窗滤波器设计法
例题：
用Kaiser窗设计高通滤波器
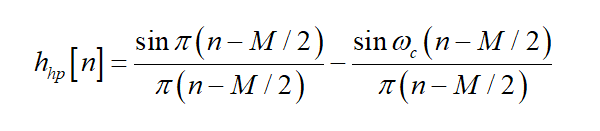
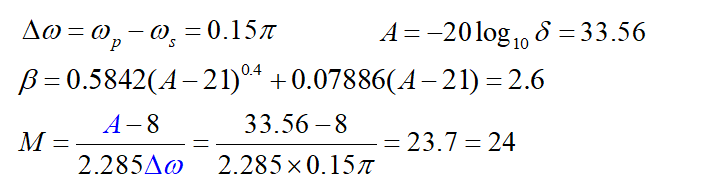
IIR和 FIR滤波器的评价
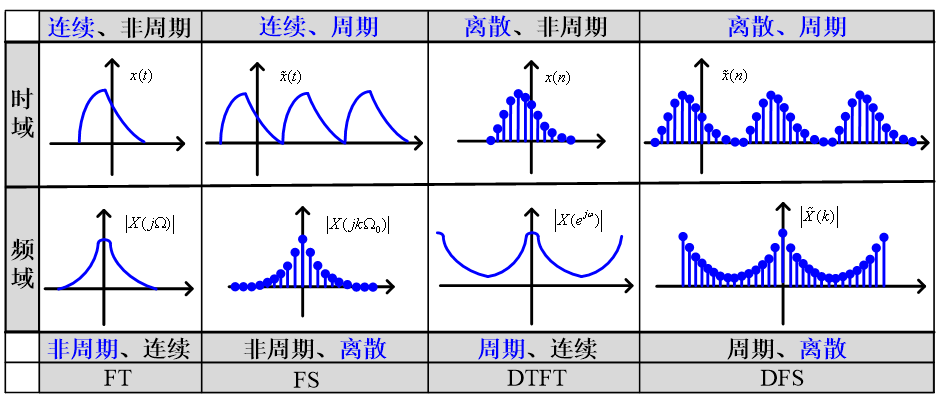
周期序列的离散傅里叶级数DFS
连续时间、连续频率 —傅里叶变换FT
连续时间、离散频率 —傅里叶级数FS
离散时间、连续频率 —序列傅里叶变换DTFT
离散时间、离散频率 —离散傅里叶级数DFS
复指数正交性：
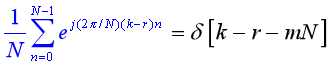
定义及性质：
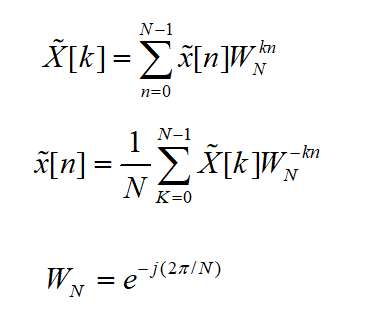
线性：
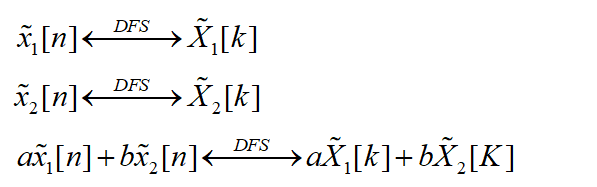
时移：
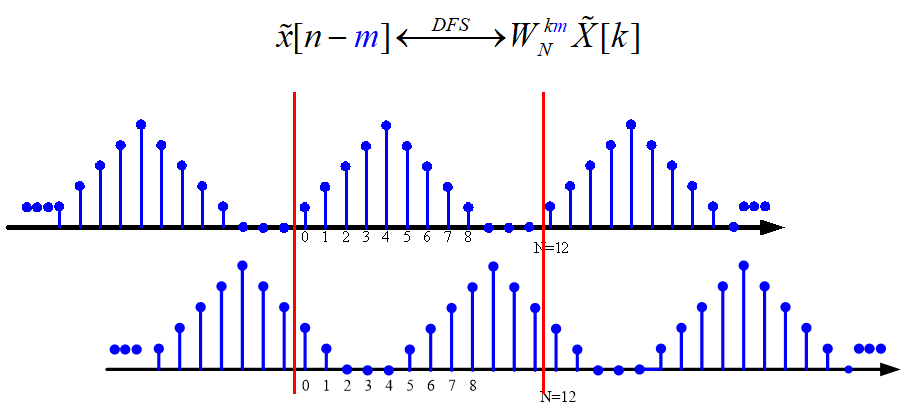
频移：
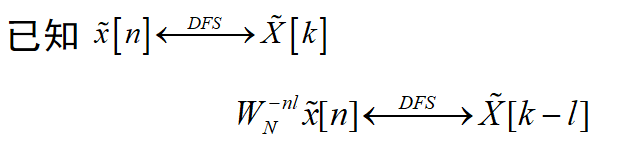
对偶性：
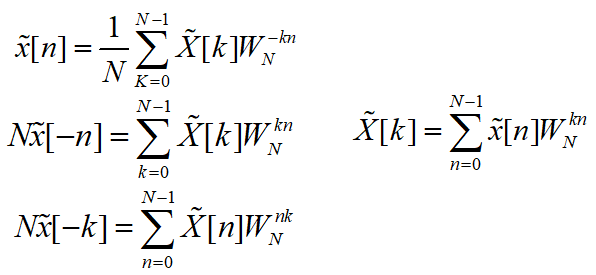
周期卷积：
注意：周期卷积与线性卷积的区别
周期信号的傅里叶变换
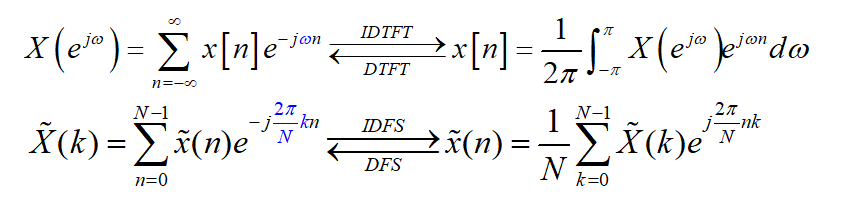
离散信号的周期化:
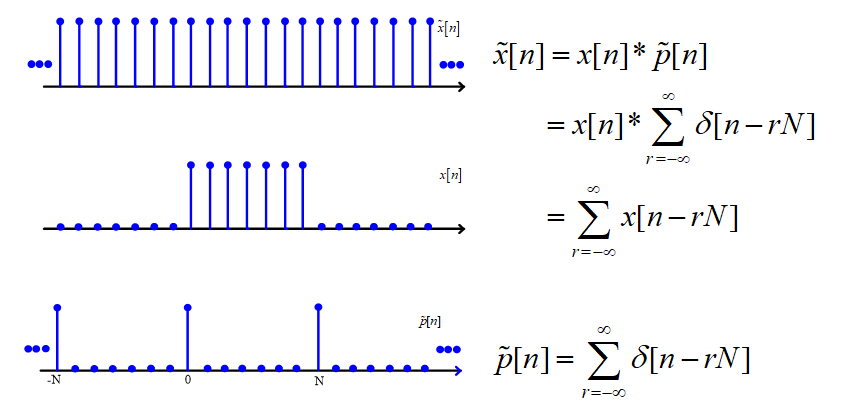
频域的冲激函数:
wechat
alipay
