数字电路与系统总结(持续更新)
数制和编码
几种常用的数制
十进制 - D
二进制 - B
八进制 - O
十六进制 - H
十进制数转换为R进制数的方法类似: 整数部分采用基数除法 小数部分采用基数乘法

二进制算数运算
二进制正负数的表示法
原码:
最高位表示正负号:0表示正, 1表示负 ; 其余各位表示数的绝对值
反码:
最高位表示正负号,0表示正,1表示负
正数的反码与它的原码相同
负数的反码可通过将原码的数值位逐位求反得到
有效数字(不包含符号位)为n位的二进制数N的反码

补码:
最高位表示正负号,0表示正,1表示负
正数的补码与它的原码相同
负数的补码可通过将原码的数值位逐位求反,然后在 最低位加1得到
有效数字(不包含符号位)为n位的二进制数N的补码

补码表示的二进制数相加
和的符号位:两加数的符号位和来自最高有效位的进位相加, 舍弃产生的进位
补码加法运算应在相应位数表示的数值范围内进行
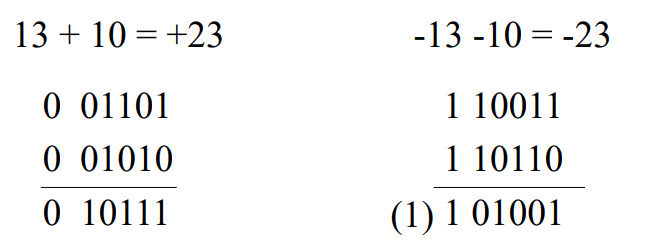

几种常用的编码
格雷码
每一位的变化按一定顺序循环:自右向左每一位状态循环中连续0、1 数目增加一倍
按照“相邻性”编码:相邻代码间只有一位变化,最大数与最小数间也仅一位变化,代码变换不会产生过渡噪声
BCD码转换成格雷码:
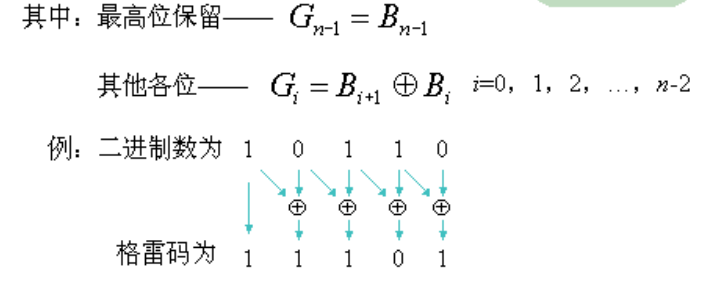

逻辑代数基础
逻辑运算的数学方法:布尔代数(开关代数、 逻辑代数)
逻辑变量与逻辑函数
逻辑代数中的变量称为 逻辑变量
用字母A、B、C、…表示
只能有两种可能的取值:真或假
常把真记作“1”,假记作“0”
“1”和“0”不表示数量的大小,表示完全对立的两种状态
逻辑代数中的三种基本运算
基本逻辑运算:
逻辑与(逻辑相乘,AND)
表达式: Y=A·B=AB; “·”为逻辑与运算符 也可以省略
逻辑与的含义:只有当决定一件事情的所有条件都 部具备时,这件事情才会发生
在逻辑电路中,把能实现与运算的基本单元叫作 与门

逻辑或(逻辑相加,OR)
表达式: Y=A+B; “+”为或运算 符
逻辑或的含义:在决定一件事情的各条件中,只要有一个 或一个以上条件具备,这件事情就发生
在逻辑电路中,把能实现或运算的基本单元叫作 或门

逻辑非(逻辑求反,NOT)
表达式: Y=A’;读作A非
逻辑非的含义:当条件不具备时,事情才会发生
在逻辑电路中,把实现非运算的基本单元叫作 非门(反相器)

复合逻辑运算
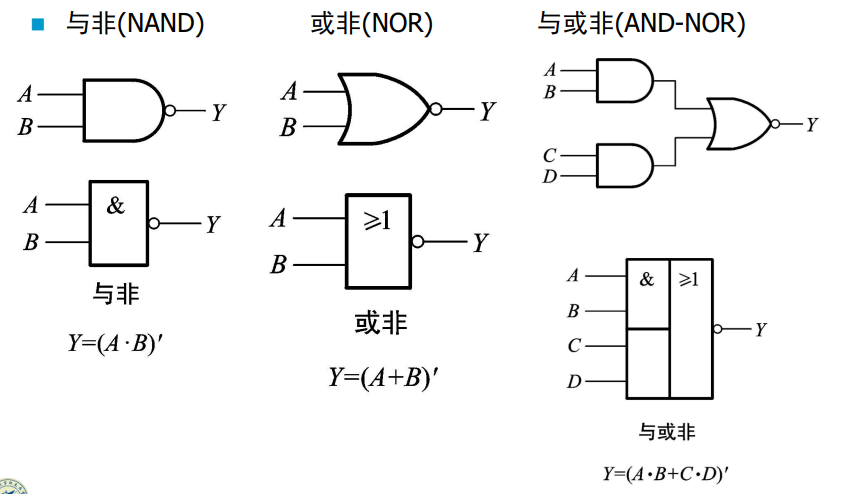
异或:
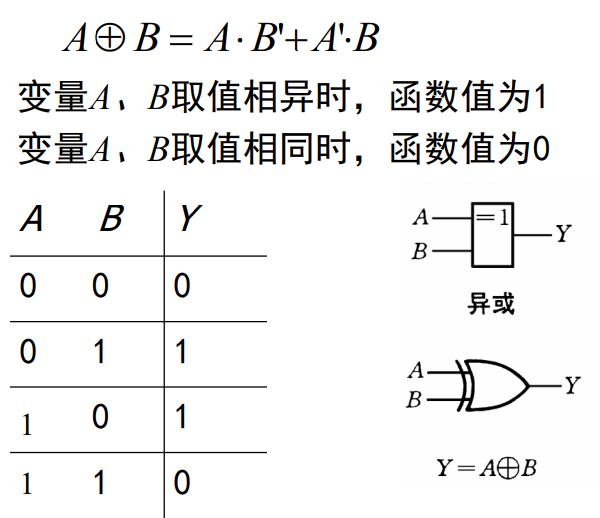
同或:

逻辑运算的优先顺序:
(1)圆括号 (2)非运算 (3)与运算 (4)或运算
逻辑代数的基本公式和常用公式

逻辑代数的基本定理
代入定理
在任何逻辑等式中,如果等式两边所 有出现某一变量的位置都代以一个逻辑式,则等式仍然成立
代入规则可以用来扩大基本公式和常 用公式的应用范围
反演定理
求Y的反函数 :将函数式中所有的“·” 换成“+” , “+”换成“·”; “0”换 成“1” , “1”换成“0”;原变量换成反变量,反变量换成原变量
注意:
•变换时要保持原式中逻辑运算的优先顺序
•不是一个变量上的反号应保持不变
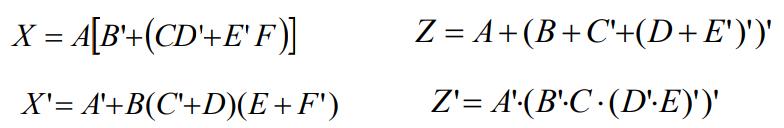
对偶定理
求Y的对偶式 :将式中所有的“·”换成 “+” , “+”换成“·”; “1”换成“0” , “0”换成“1”
注意:
• 原变量反变量保持不变
• 变换时要保持原式中逻辑运算的优先顺序
如果两个逻辑表达式相等,那么 它们的对偶式也相等
逻辑函数及其描述方法
逻辑函数的描述
逻辑函数 (logic function) (二值逻辑函数):
逻辑关系中输出与输入间的函数关系 Y = F(A,B,C,…)
逻辑函数的表示方法: 逻辑真值表、逻辑函数式、逻辑图、波形图、 卡诺图、硬件描述语言
描述方法间的相互转换
由逻辑表达式列出真值表
由真值表写出逻辑表达式
由逻辑式画出逻辑图
由逻辑图写出逻辑式
逻辑函数的两种标准形式
函数的最小项及其性质
最小项 :
在一个有n个变量的逻辑函数中,包含全部n个变量的乘积项称为最小项m,其中每个变量必须而且只能以原变量或反变量的形式出现一次。
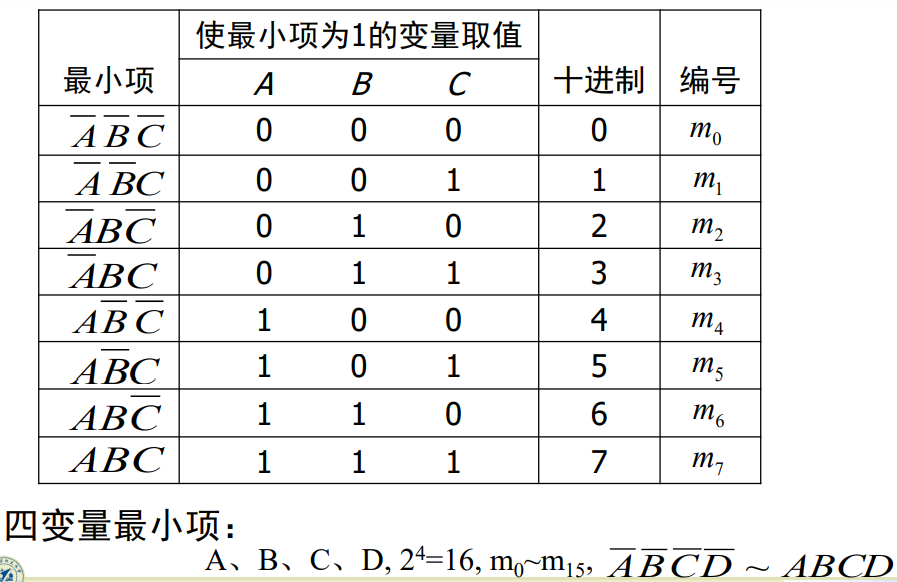
性质:
每一个最小项与变量的一组取值相对应,只有该组 取值才使其为1
任意两个最小项的乘积恒为0
全体最小项之和恒为1
具有相邻性(逻辑相邻)的两个最小项之和可以合并成一项并消去一对因子。
逻辑函数的最小项之和形式(标准与或表达式) :
每个与项都是最小项的与或表达式,称为标准与或表达式,也称为最小项之和表达式
从真值表求标准与或表达式
从一般与或表达式求标准与或表达式
对于任何一个逻辑函数,它的真值表是唯一的,因而它的标准与或式也是唯一的
函数的最大项及其性质
最大项 :
在一个有n个变量的逻辑函数中,包括 全部n个变量的和项称为最大项M,其中每个变量必须而且只能以原变量或反变量形式出现一次。
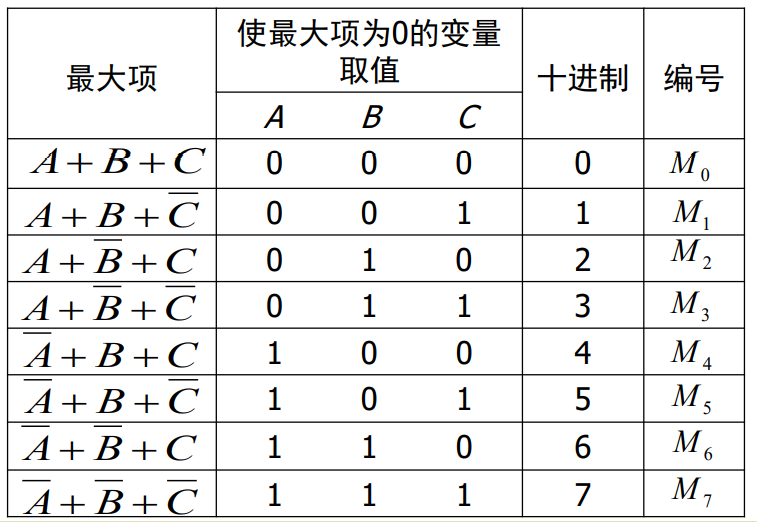
性质:
每一个最大项与变量的一组取值对应, 即只有这一组取值才使该最大项为0
任意两个最大项之和恒为1
所有最大项之积恒为0
只有一个变量不同的两个最大项的乘积等于各相同变量之和
最大项与最小项关系:摩根定律
逻辑函数的最大项之积形式(标准或与表达式) :
每个或项都是最大项的或与表达式称为标准或 与表达式,也称为最大项之积表达式
从函数真值表求标准或与表达式
在真值表中找出使逻辑函数Y为0的行
对于Y=0的行,写出对应的最大项
每个使函数Y为0的变量取值组合对应一个最大项, 其中取值为0的写入原变量,取值为1的写入反变量
将所得到的最大项相与
逻辑函数的化简方法
逻辑函数的最简形式
同一个逻辑函数可以写成各种不同形式的表达式:
表达式越简单,所表示的逻辑关系越明显,可用越少的电子器件来实现
需要通过化简的方法找出逻辑函数的最简形式
判别与或表达式是否最简的条件:
乘积项(与项)最少
每个乘积项中变量最少
常用的化简方法
公式化简法
并项法

吸收法

消项法

消因子法

配项法

卡诺图化简法
卡诺图是由美国工程师卡诺首先提出的一种 用来描述逻辑函数的特殊方格图。 n变量最小项的卡诺图:将n变量的全部最小 项各用一个小方格表示,而且几何相邻的小方 格具有逻辑相邻性,即两相邻小方格所代表的 最小项只有一个变量取值不同。
特点:
卡诺图中的小方格数等于最小项总数,若逻辑函 数的变量数为n,则小方格数为2^n^个
卡诺图行列两侧标注的0和1表示使对应方格内最小项为1的变量取值。同时,这些0和1组成的二 进制数大小就是对应最小项的编号。
在卡诺图中,几何相邻的最小项具有逻辑相邻性。 因此,变量的取值按循环码(格雷码)排列
卡诺图几何相邻:相邻;对称(上下或左右)
变量应按顺序分组
逻辑函数的卡诺图表示法:
根据逻辑函数的逻辑式画出其卡诺图,先把函数写成最小项之和的形式,然后在卡诺图上与这些最小项对应的位置上填入1,在 其余位置上填入0,这样就可得到该逻辑函数的卡诺图。
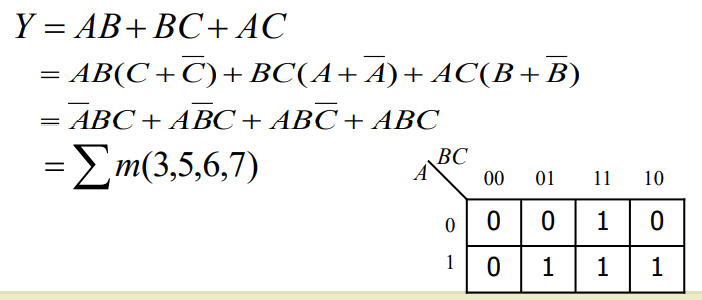
逻辑函数的卡诺图化简法(图形化简法)
具有相邻性的最小项可以合并,并消去不同的因子。
规则1:卡诺图中两个(2^1^)相邻1格(方格为1)的最 小项可以合并成一个与项,并消去一个变量。
规则2:卡诺图中四个(2^2^)相邻1格的最小项可以合 并成一个与项,并消去两个变量。
卡诺图中,如果有2^n^个最小项相邻(n=1,2,…) 并排列成一个矩形组,则它们可以合并为一 项,并消去n个因子。合并后的结果中仅包含这些最小项的公共因子
用卡诺图化简法求最简与或表达式
画出函数的卡诺图
合并最小项
写出最简与或表达式
用卡诺图化简,关键是画圈,五个规则:
(1) 1格不能漏圈;
(2) 1格允许被一个以上的圈所包围; (A+A=A)
(3) 圈的个数尽可能少; (乘积项最少)
(4) 圈的面积尽可能大; (乘积项包含的因子最少)
(5) 每个圈至少应包含一个新的1格
卡诺图化简得到的最简与或式不 一定是唯一的
合并卡诺图中的0,通过合并卡诺图中的0化简函数,求反函数的最简与或式,求函数最简与或非式
具有无关项的逻辑函数及其化简
具有约束项的逻辑函数(输入逻辑变量的某些取值组合禁止出现)
对应的最小项称为约束项(恒等于0)
输入逻辑变量的某些取值组合出现时,输出逻辑值可以是任意的(0或1)
对应的最小项称为任意项
卡诺图中常用符号“×”或“φ”表示,可以认为是1或0
合并最小项时,究竟把卡诺图上的×作为1 (即认为函数式中 包含了这个最小项)还是0(即认为函数式中不包含这个最小 项)对待,应以得到的相邻最小项矩形组合最大、而且矩形 组合数目最少为原则。
多输出逻辑函数的化简
不应孤立求出每个输出函数的最简式
利用共用项,总体最简(门数和总输入端数最少)
所用门电路数目减少,连线数目减少
逻辑函数形式的变换
与—或 → 与非 — 与非
将与或式两次求反,再使用一次摩根定理(反演定理)

与—或 → 与或非
用摩根定理变换
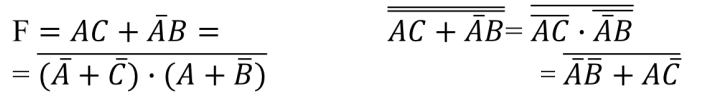
与—或 → 或非 — 或非
首先得到与或非形式,然后利用反演定理将其中的每个乘积项化为或非形式。
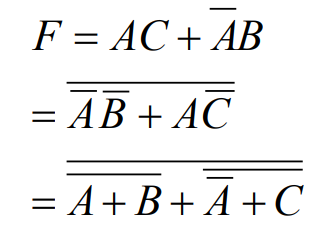
小结
• 数制和码制、逻辑代数的基本运算公式和定律、逻辑函数的表示形式及化简方法
• 二进制、八进制、十六进制和十进制,各种计数体制之间的转换。BCD码、格雷码(Gray)、校验码和字符编码 三种基本运算,与、或、非
• 逻辑函数真值表、表达式、卡诺图、逻辑图等常用的表示方法,各具特点并可以相互转换
• 逻辑函数化简的方法主要有公式法和卡诺图法
• 卡诺图法特点是简单、直观,不易出错,但是化简的逻辑变量不能太多
• 除了上述两种基本的化简方法之外,对于较多变量的复杂逻辑函数,可采用计算机辅助化简,目前已有多种实用的逻辑化简分析工具或软件
门电路
概述
门电路(Gate Circuit) / 逻辑门(Logic Gate)
• 数字集成电路中实现基本逻辑运算 和复合逻辑运算的单元电路
• 常用门电路:与门、或门、非门、 与非门、或非门、与或非门、异或门等
基本开关电路
• 获得高、低电平
• 单开关电路:功耗较大
• 互补开关电路:功耗极小
正逻辑与负逻辑
高低电平允许一定范围,数字电路中对元器件参数精度和电源稳定度要求不高
数字电路运算精度通过增加数字信号的位数达到
半导体二极管门电路
半导体二极管(Diode)的开关特性
近似伏安特性与等效电路
VCC 和 RL 很小, VON 和 RD 不能忽略(a)
VON 不能忽略, RD 可以忽略(b)
• 硅二极管,外加正向电压大于导通电压VON=0.7V, 则导通,导通后其压降保持在0.7V不变;
• 外加电压小于电压0.7V时,则截止,截止后近似认 为其电流为0,如同断开了的开关。
VON 和 RD 可以忽略(c)
二极管的动态开关特性
PN结上电荷的建立和消散有一个过程,二极管从导通到截止需要一个恢复时间。通常把它称 为反向恢复时间 ,一般在纳秒数量级,它 的存在限制了二极管的工作速度。
二极管门电路
二极管与门电路
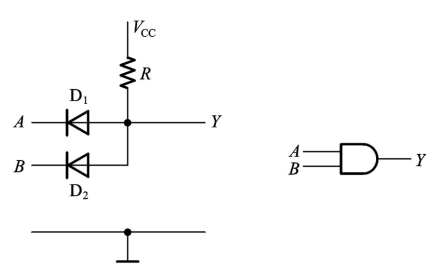
缺点:
•输出高、低电平偏移
•负载电阻的改变会影响输出的高电平
二极管或门电路
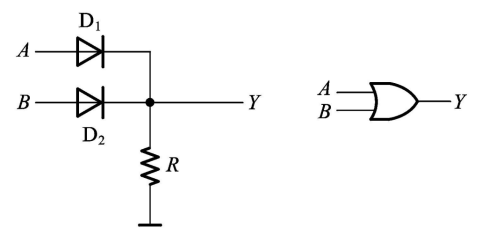
缺点:
•输出电平偏移
CMOS门电路
MOS管的输入特性和输出特性
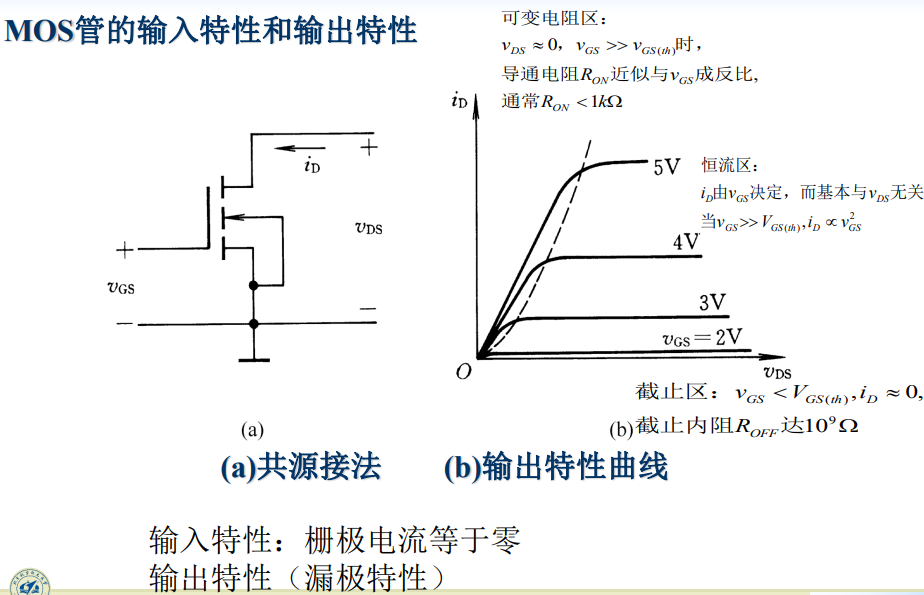
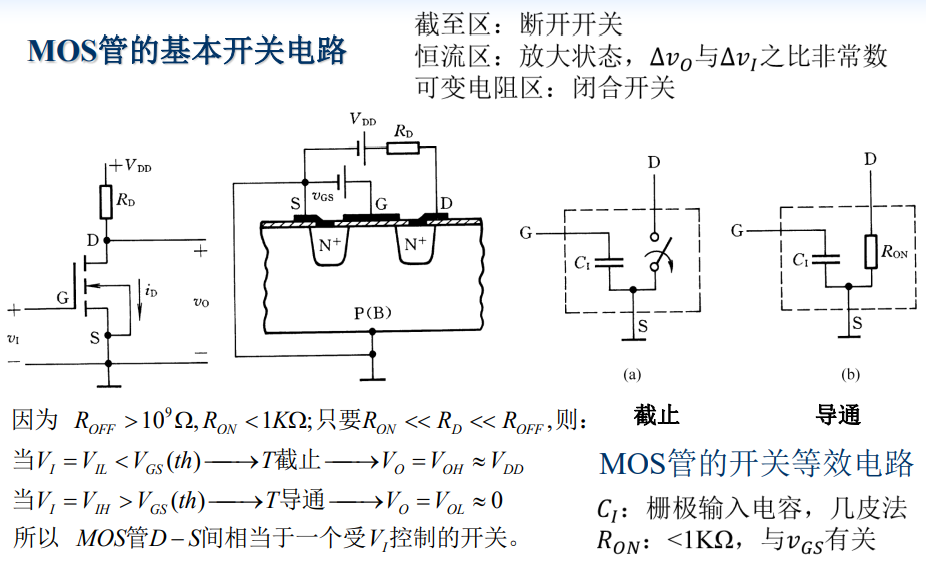
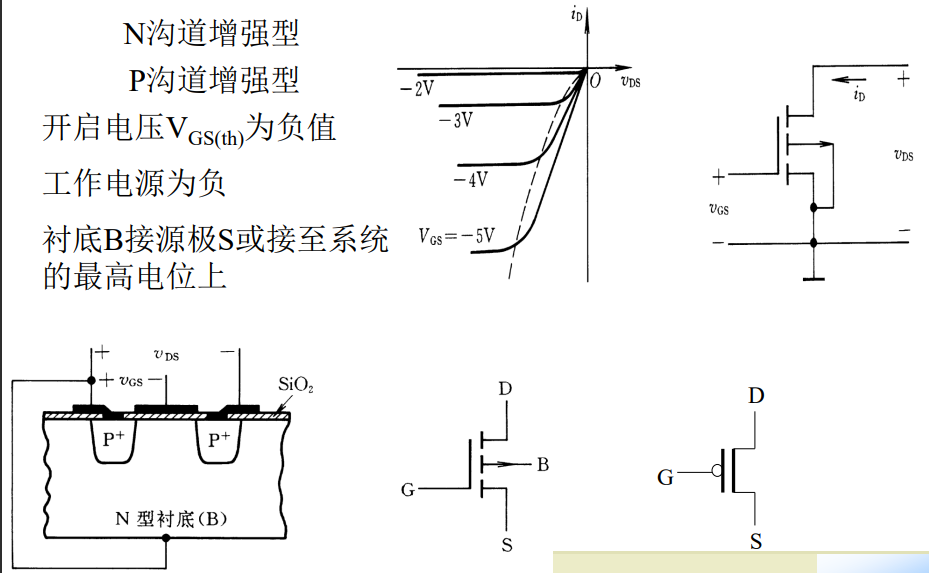
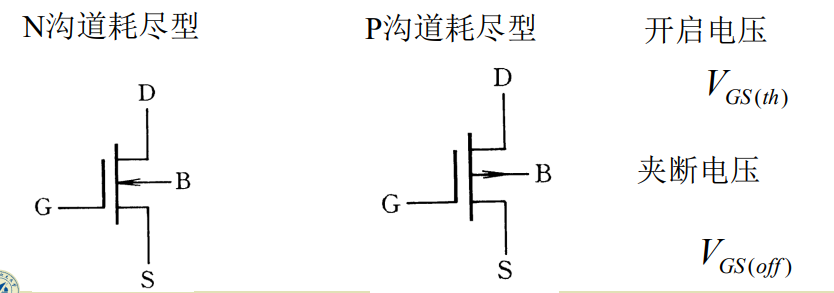
MOS管的四种类型
CMOS非门
CMOS逻辑门由参数对称的 增强型N沟道和P沟道 MOSFET构成,通常称为互补型MOS逻辑电路
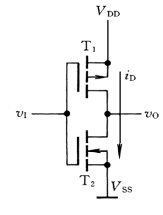
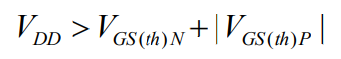
电压传输特性:
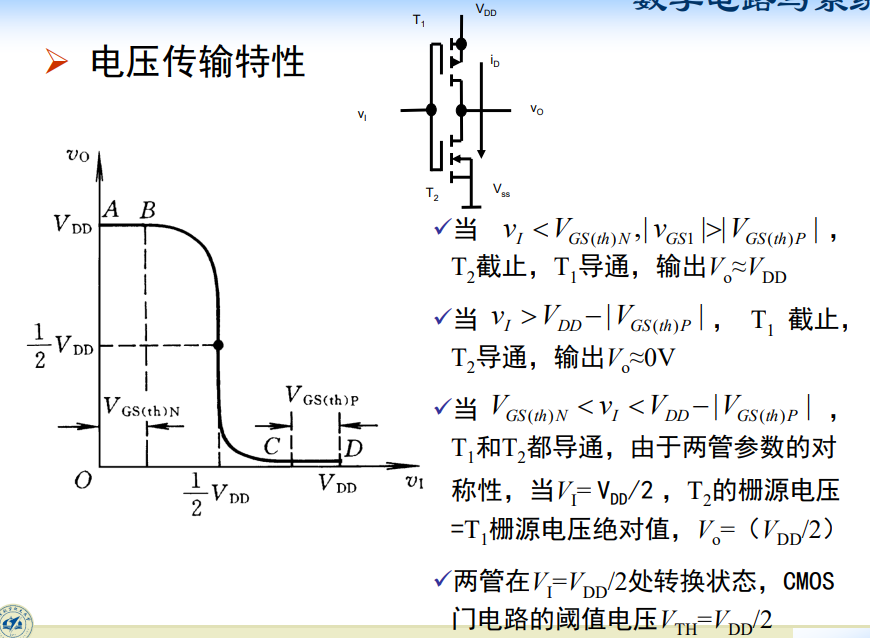
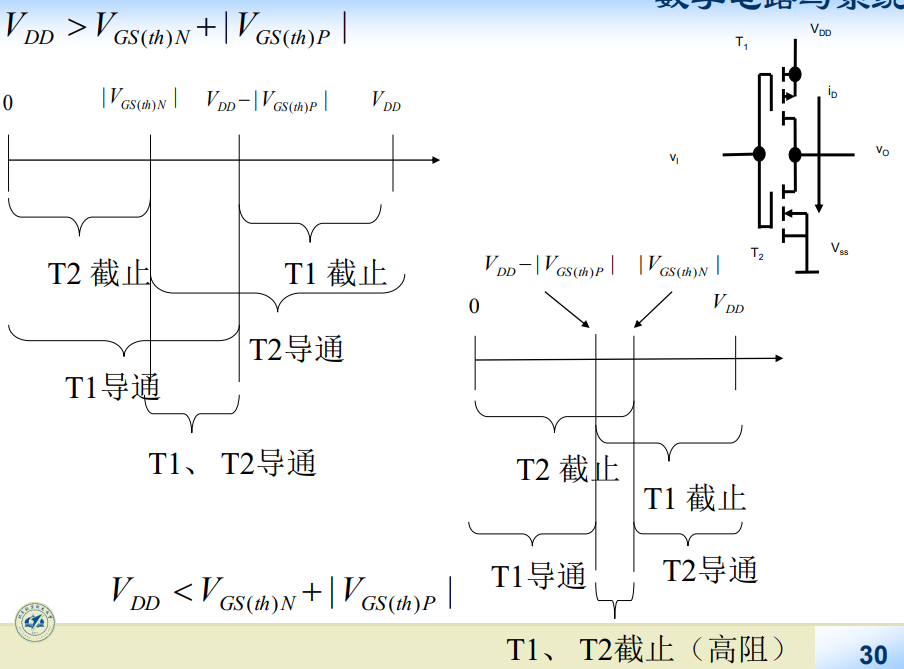
电流传输特性:
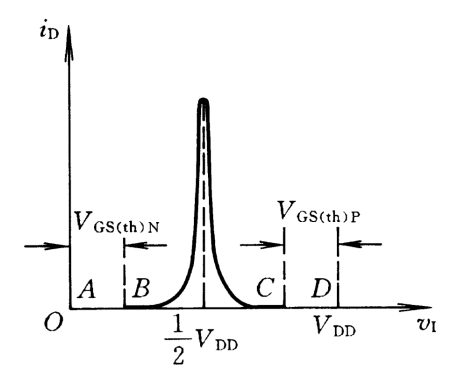
输入噪声容限:
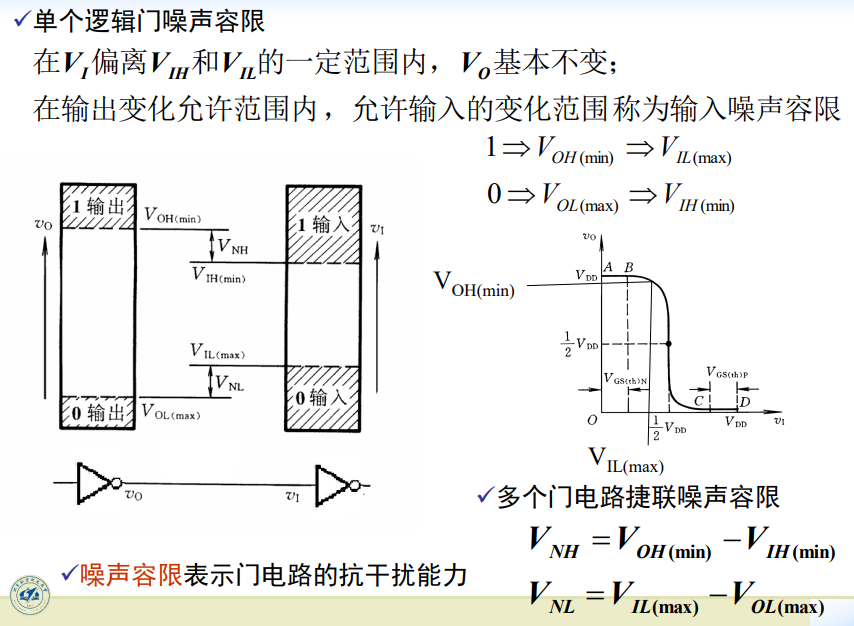
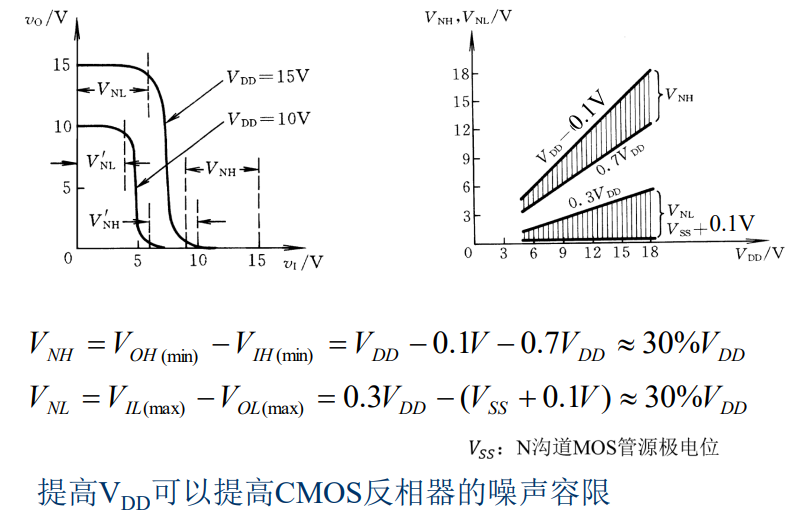
静态输入特性:
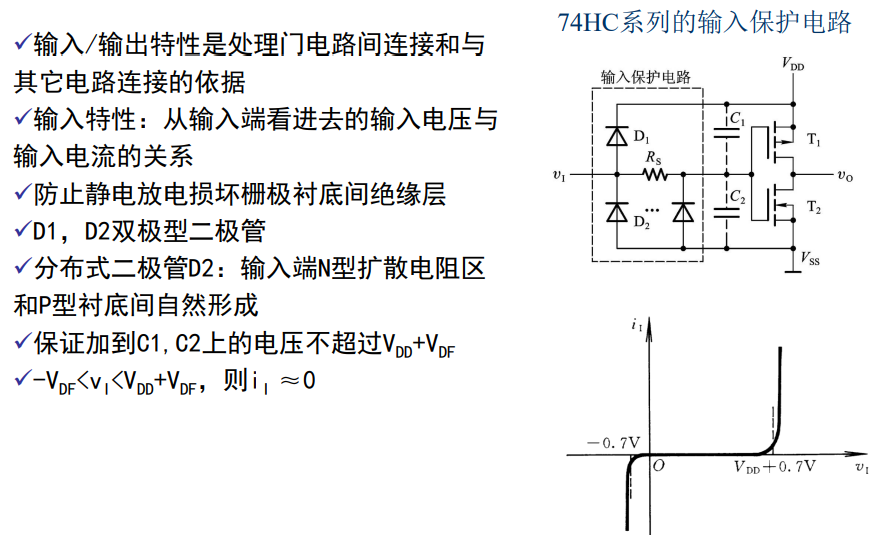
静态输出特性:
低电平输出特性:
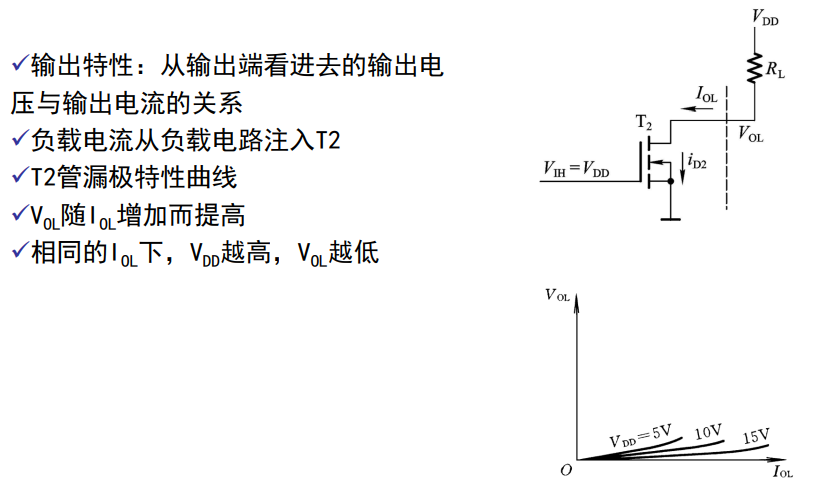
高电平输出特性:


动态特性:
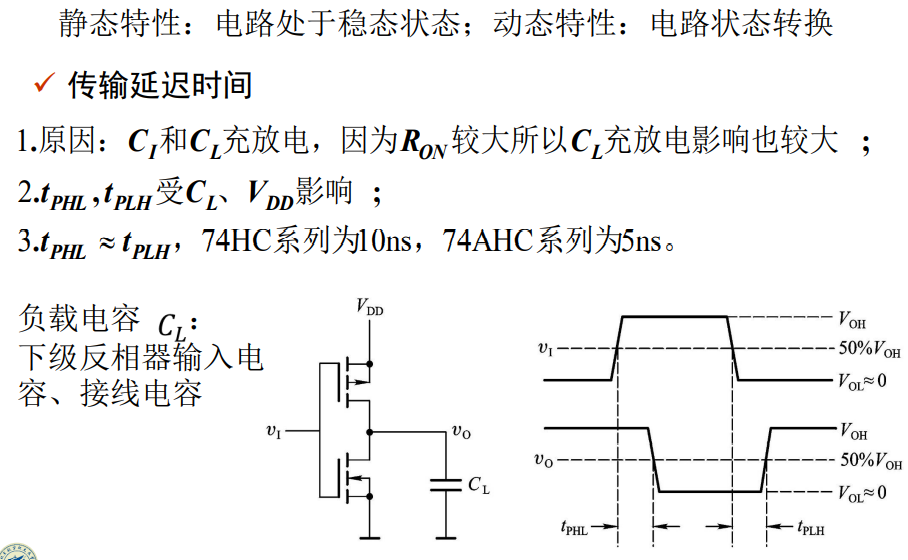
交流噪声容限:

动态功耗:

扇出数:

其他的CMOS门电路
与非门:
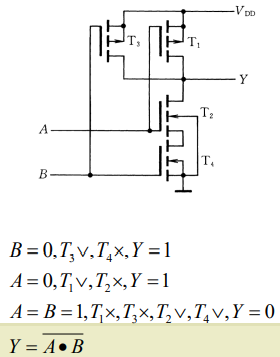
或非门:
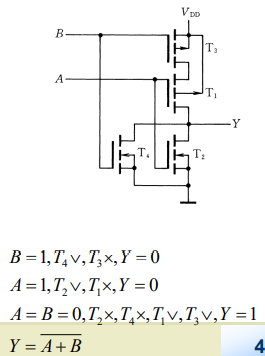
无缓冲级的CMOS门电路的缺陷:
输出电阻Ro受输入端状态的影响
输出高/低电平受输入端数目的影响 输入端数目增加时,与非门串联的NMOS管数目要增加,引起输出低电 平变高;或非门串联的PMOS管数目增加,引起输出高电平变低
输入端工作状态不同对电压传输特性的影响
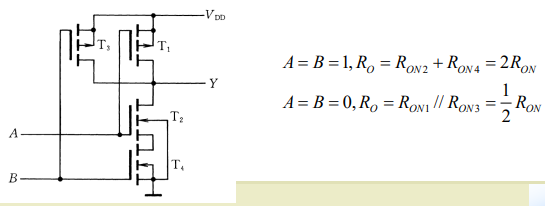
带缓冲级的与非门:
4000和74HC系列CMOS门电路中在输入输出端 分别加入反相器作缓冲级
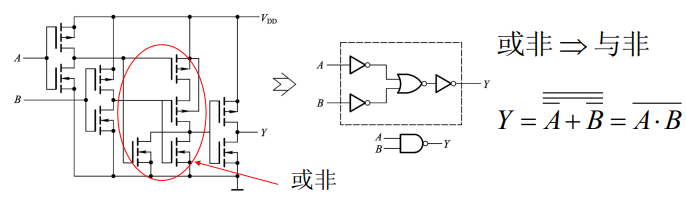
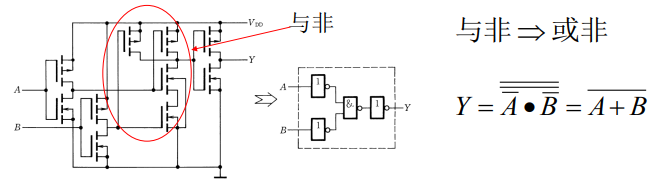
输出电阻、高低电平、电压传输特性不受输入端状态的影响
电压传输特性的转折区更陡
反相器的输入输出特性对其它门电路仍适用
漏极开路输出门电路(OD门):
把输入的电平(VDD1/0V)转换为输出电平 (VDD2/0V)
线与逻辑
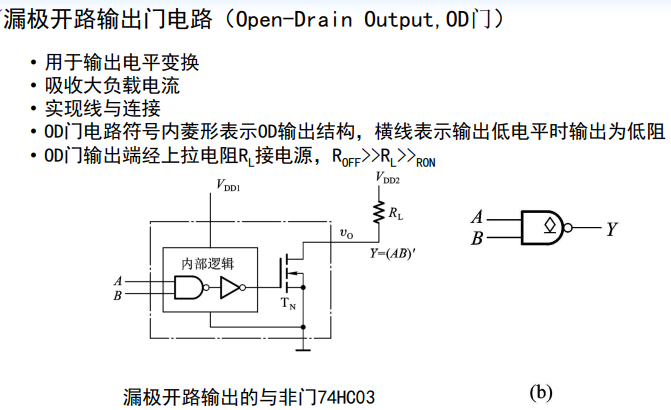
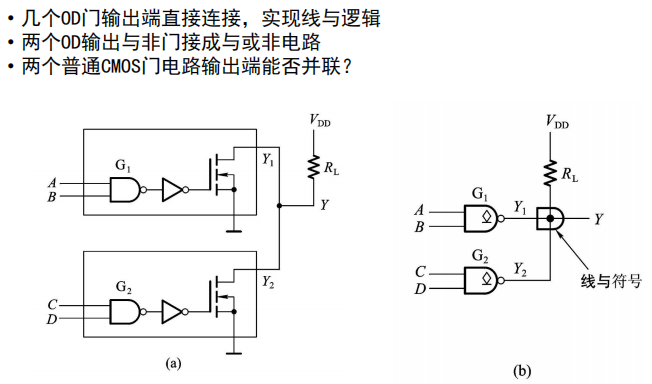
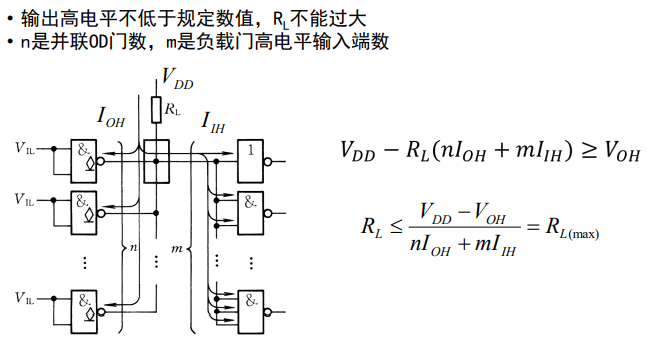
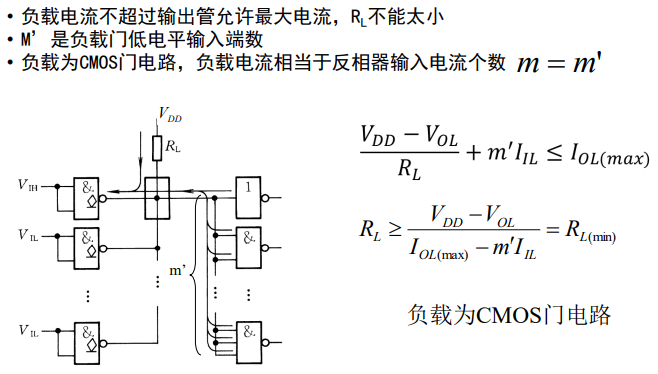
OD门线与连接中外接电阻RL阻值计算方法:
CMOS传输门:
CMOS传输门的电路结构和逻辑符号:
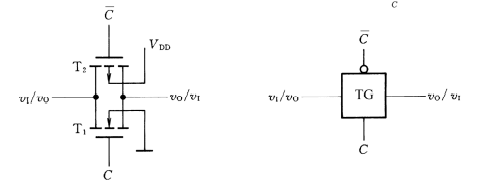
C和C’互为相反的控制信号:若控制信号是0,输出为输入的反;若控制信号是1,输出为输入

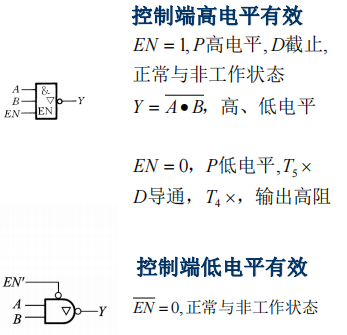
三态输出的CMOS门电路(三态门):
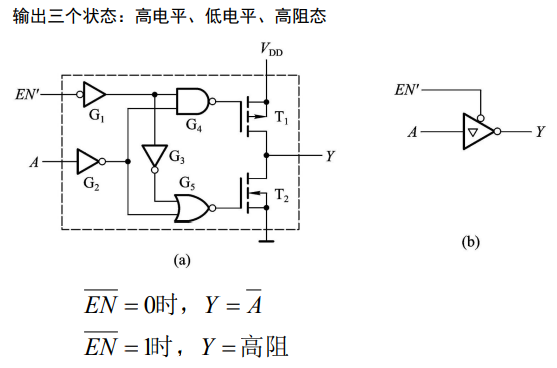
• 集成电路的输出端–输出缓冲器(Output Buffer)
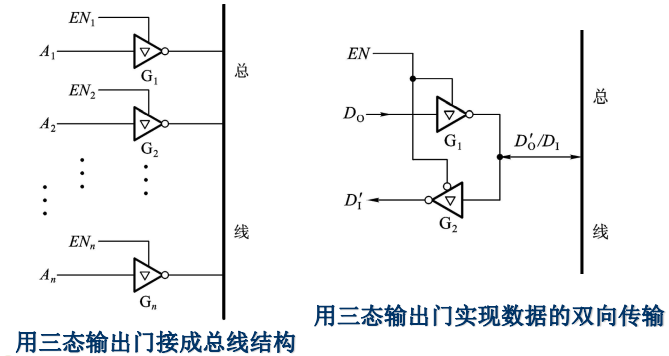
• 实现若干个门电路输出信号分时传递 – 总线结构
• 实现总线与电路的数据双向传输
CMOS集成电路的正确使用

TTL门电路
双极型三极管的开关特性
输入特性曲线
VON :开启电压 硅管,0.5 ~ 0.7V;锗管,0.2 ~ 0.3V
近似认为:VBE < V ON i B = 0 ;VBE ≥ VON iB 的大小由外电路电压、电阻决定
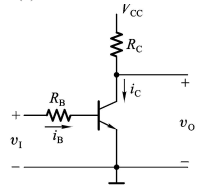
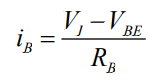
输出特性曲线
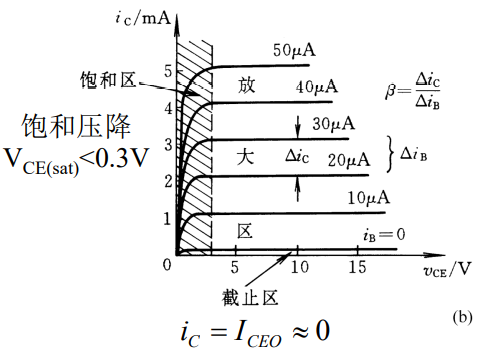

基本开关电路

开关等效电路
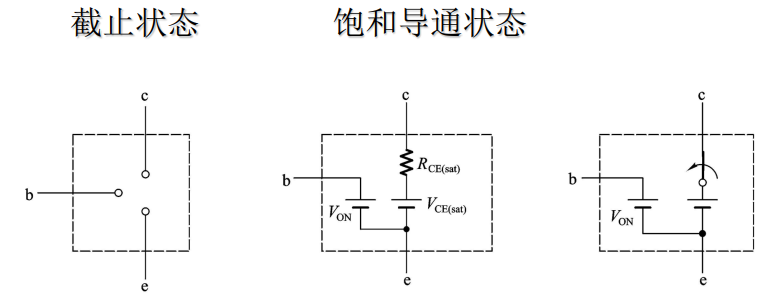
工作状态
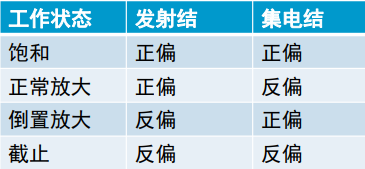
动态开关特性
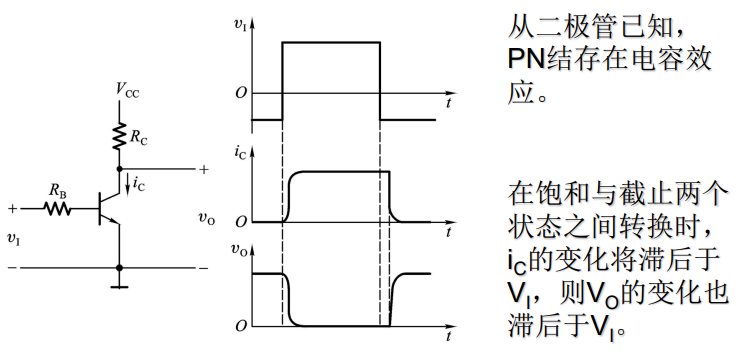
三极管门电路
三极管的基本开关电路就是非门(反相器)
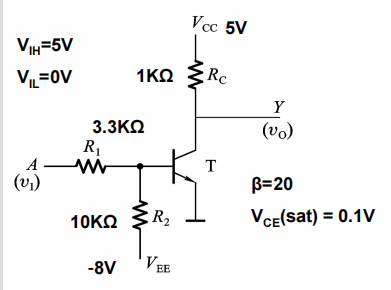
实际应用中,为保证VI=VIL 时T可靠截止,常在输入接入负压


TTL反相器的结构与原理
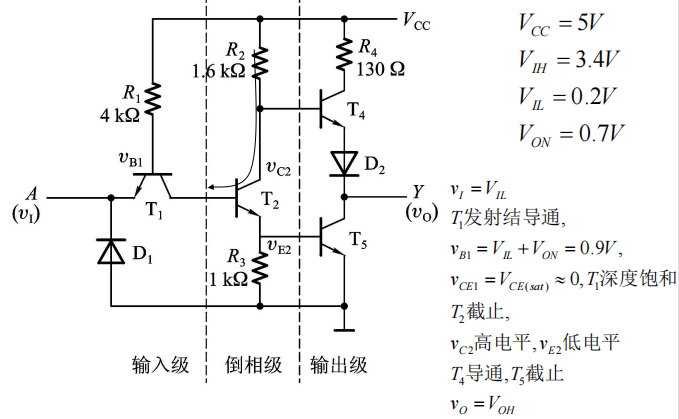
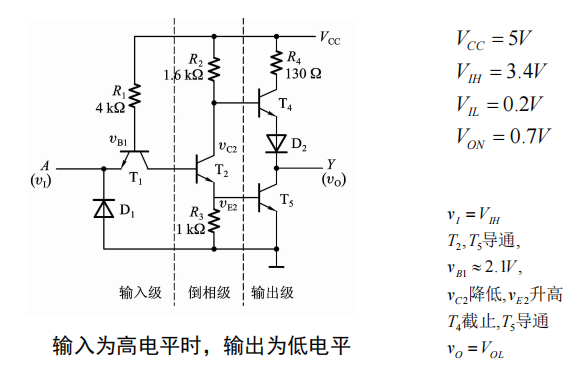
74系列TTL反相器的典型电路
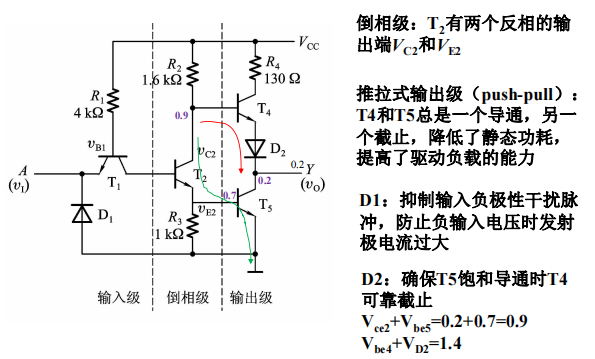
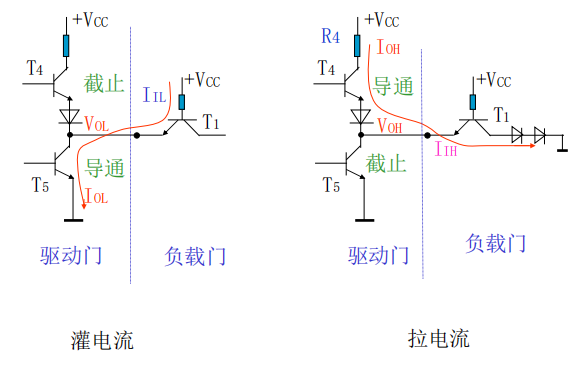
TTL非门传输延迟
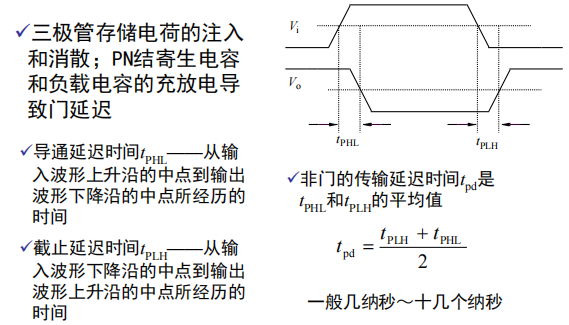
其他类型TTL门电路
与非门
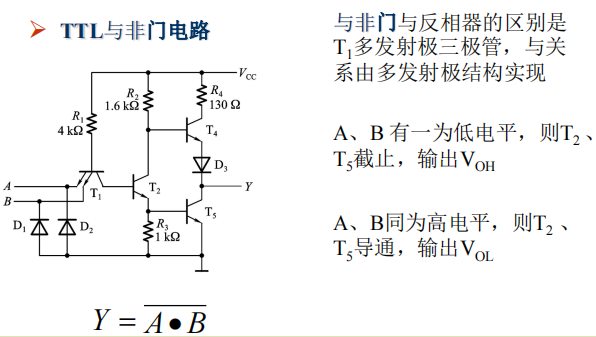
与非门每个输入端电流的计算:
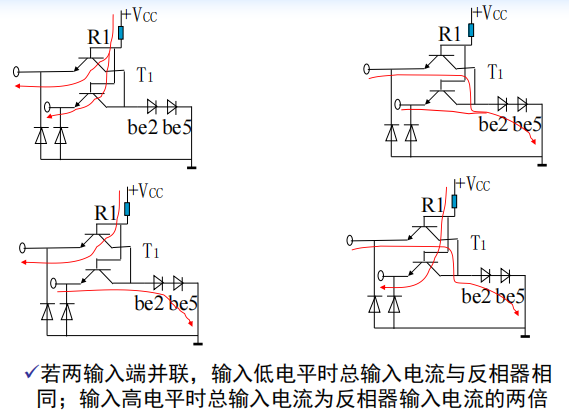
或非门
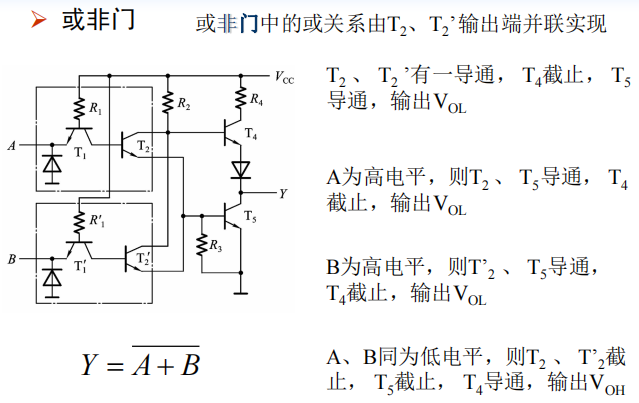
与或非门
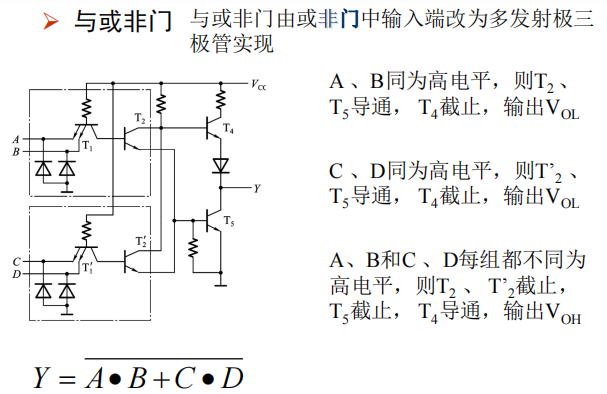
异或门
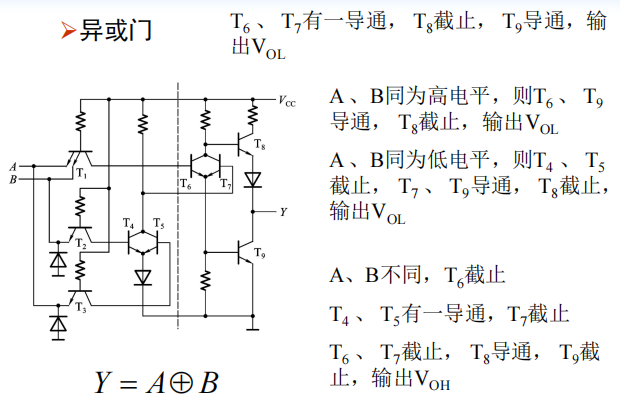
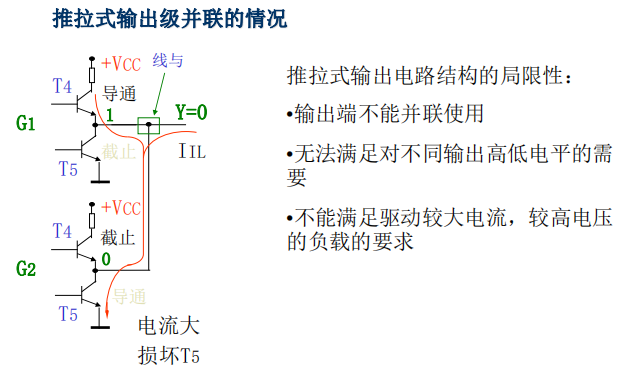
集电极开路的门电路(OC门)
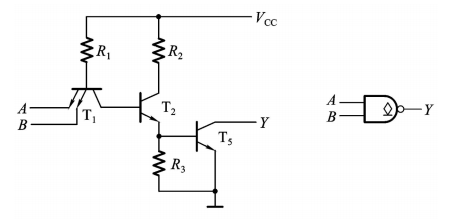
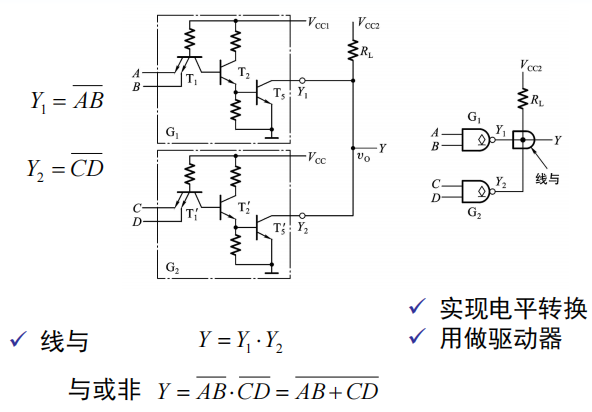
外接负载电阻RL的计算

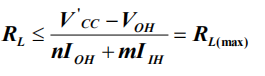
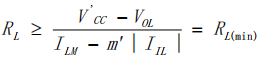
三态输出门(TS门)
组合逻辑电路
数字系统由数字电路模块构成,这些模块可分为两大类:组合逻辑电路;时序逻辑电路
组合逻辑电路(combinational logic circuit):
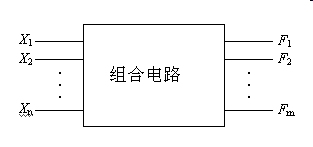
逻辑功能特点——功能上,任意时刻的输出仅取决于该时刻的输入
电路结构特点——电路结构上不含记忆(存储)元件
时序逻辑电路(sequential logic circuit):
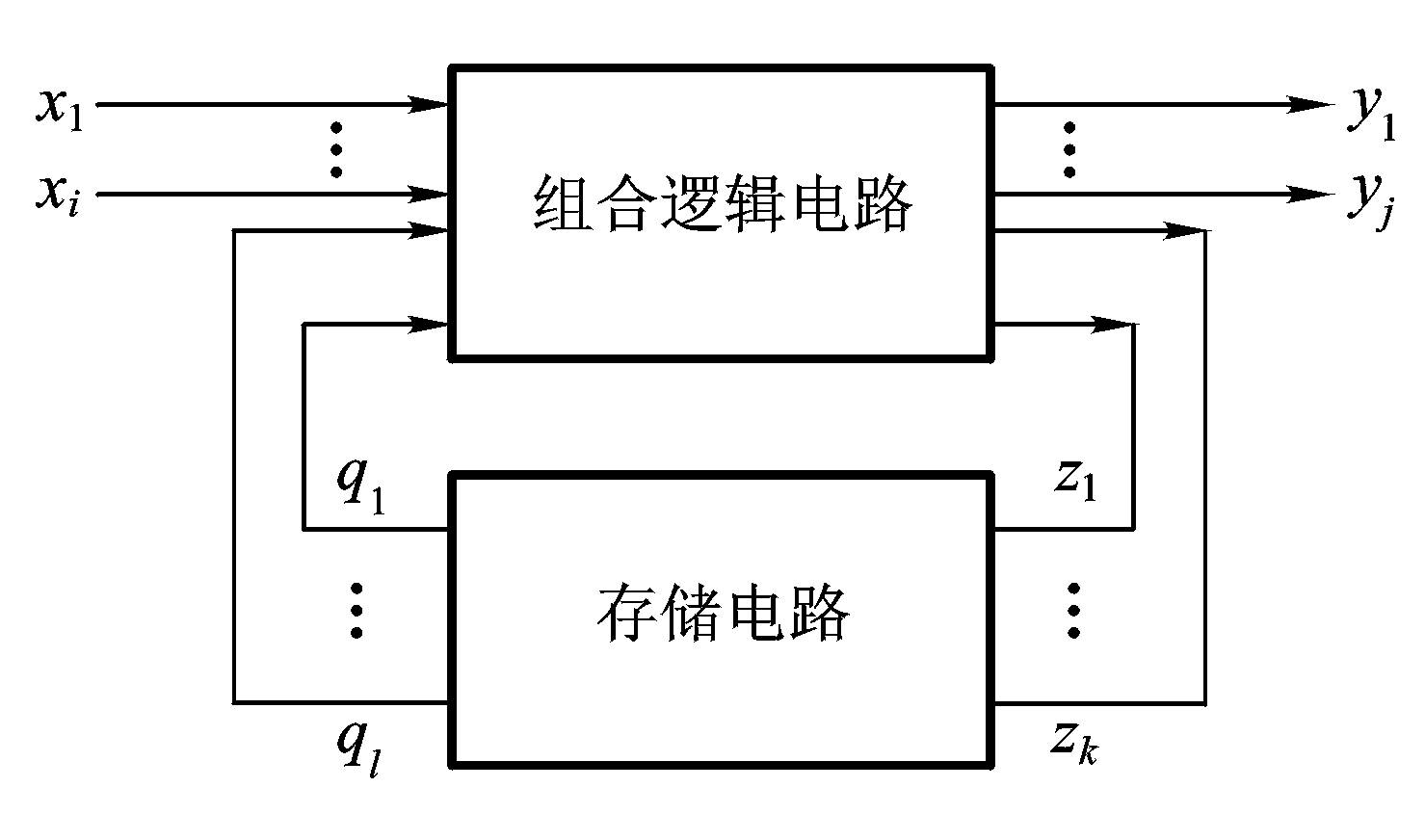
功能上:任一时刻的输出不仅取决于该时刻的输入,还与电路原来的状态有关
电路结构上①包含存储电路和组合电路 ②存储器状态和输入变量共同决定输出
组合逻辑电路的分析方法
组合逻辑电路的分析是用逻辑函数来描述已知的电路,找出输入、输出间的关系,从而判断电路功能

组合逻辑电路的设计方法
组合逻辑电路的设计就是根据给定的逻辑要求,得出能实现设计要求的最简逻辑电路
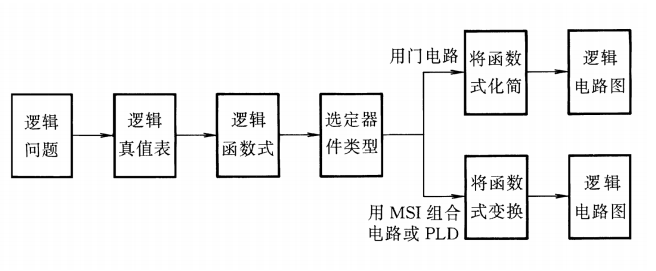
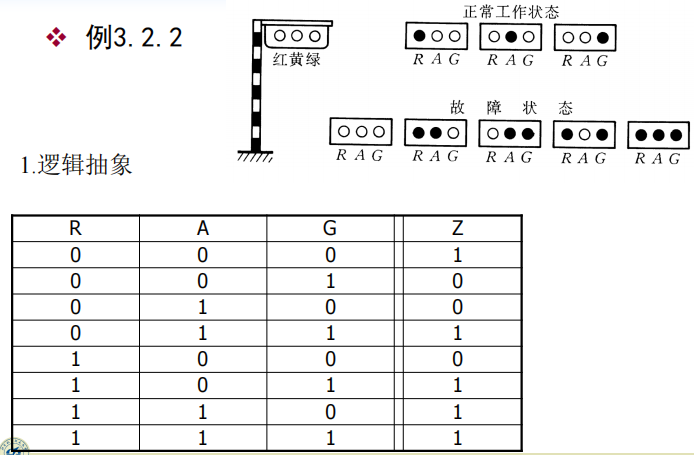
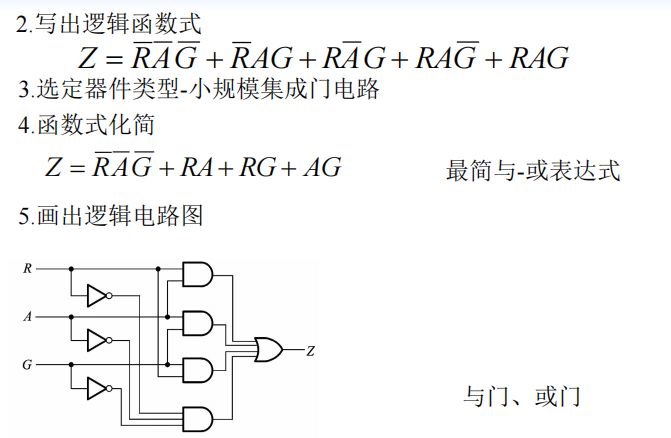
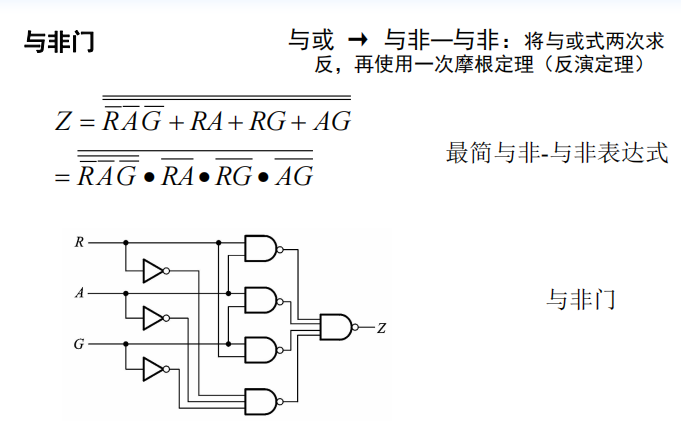
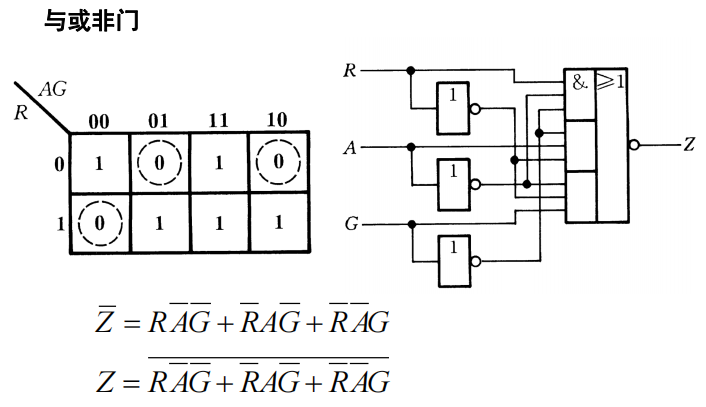
若干常用的组合逻辑电路模块
编码器(Encoder):
将字母、数字、符号等信息编成一组二进制代码
编码器将输入的每个高/低电平信号变成一个对应的二进制代码
编码器是一个多输入多输出电路
通常m个输入信号,需要n位二进制编码,m应不大于2n
常用的编码器有二进制编码器和二—十进制编码器两种
普通编码器/优先编码器
二进制编码器:
用n位二进制代码对2^n^个信号进行编码
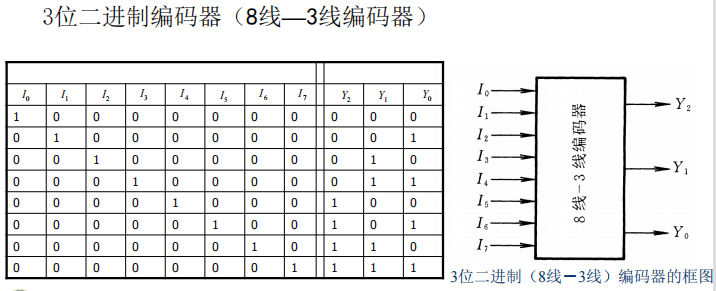
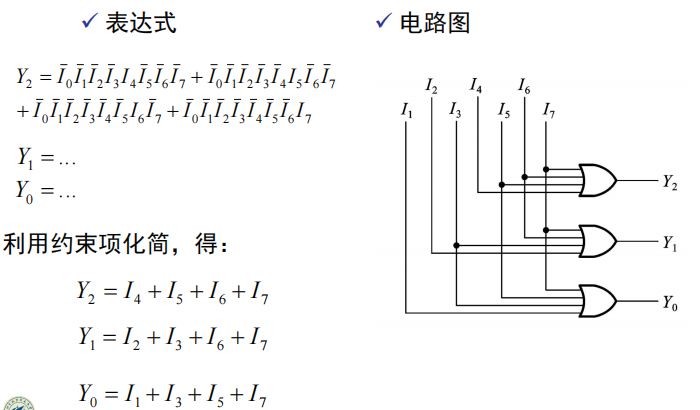
普通编码器:任何时刻只允许输入一个编码信号
优先编码器:允许同时输入两个以上的编码信号,但只对其中优先权最高的一个进行编码
逻辑框图表示中规模集成电路器件:
框图内部:标注输入输出原变量
框图外部:若为低电平有效信号,则画小圆圈并标注反变量
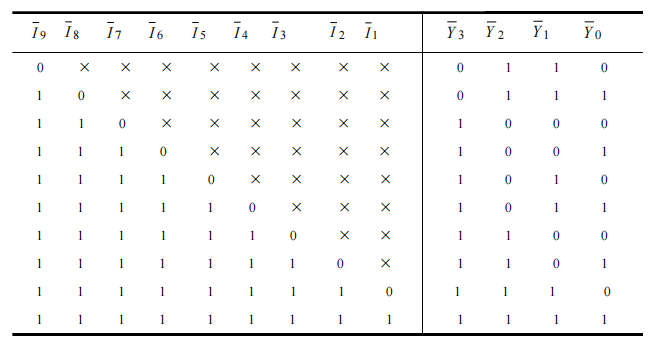
74HC148:8线—3线优先编码器
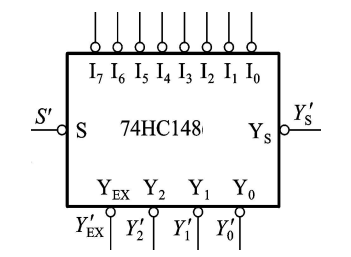
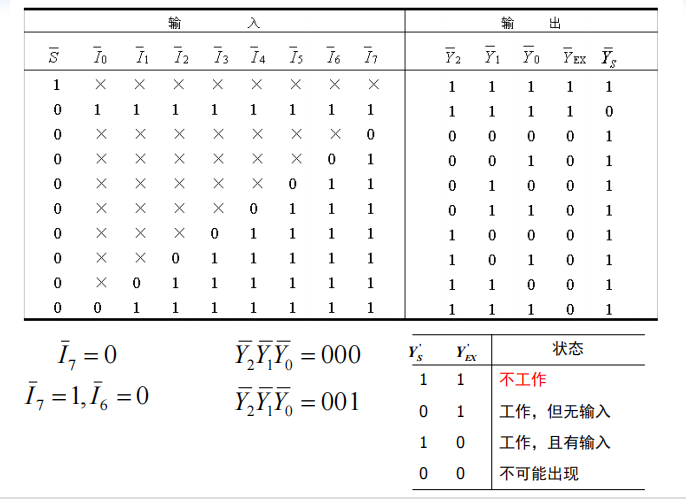
16线-4线优先编码器:
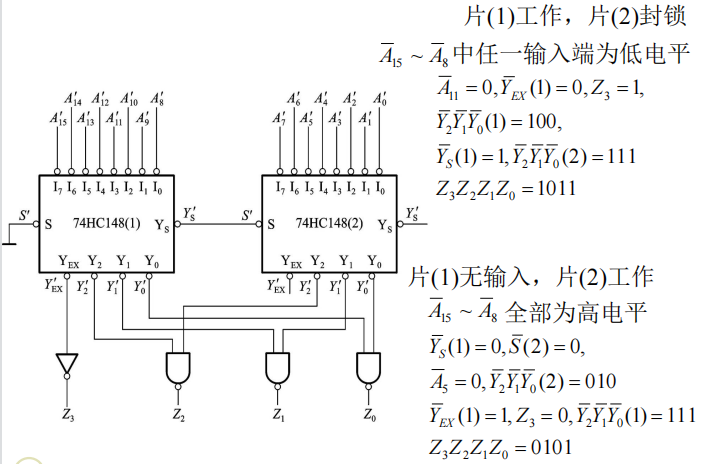
二—十进制编码器:
常用8421BCD编码器74LS147
译码器(Decoder):
与编码器相反,将每个输入的二进制代码译成对应的输出高、低电平信号或另外一个代码
常用的译码器,二进制译码器、二-十进制译码器和显示译码器
二极管与门阵列组成译码器:

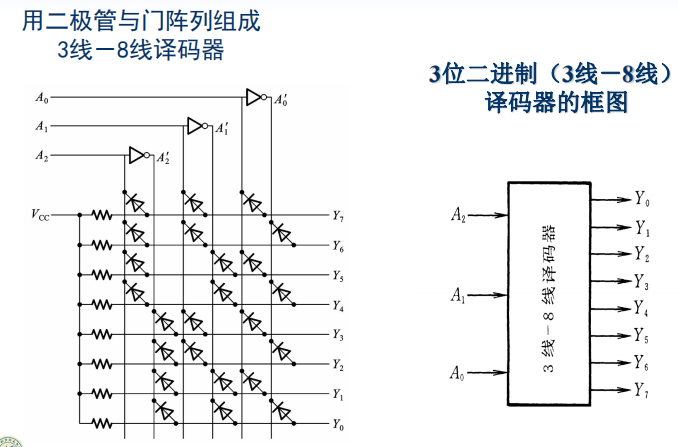
二极管与门阵列组成译码器缺点:
•输出高、低电平偏移
•输入电阻低、输出电阻高
74HC138:3线-8线译码器
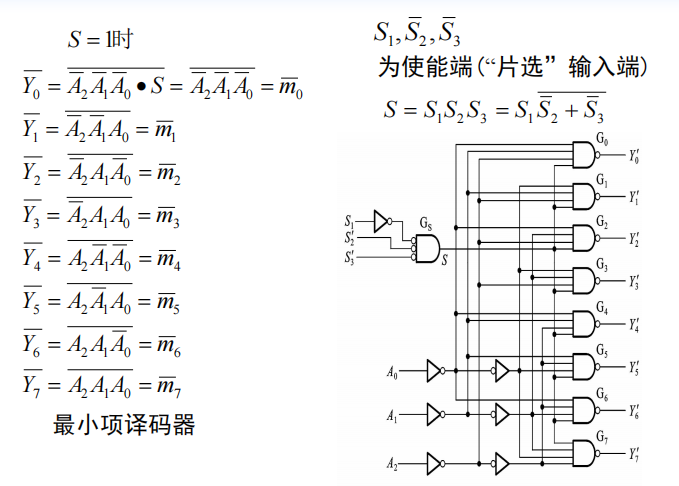
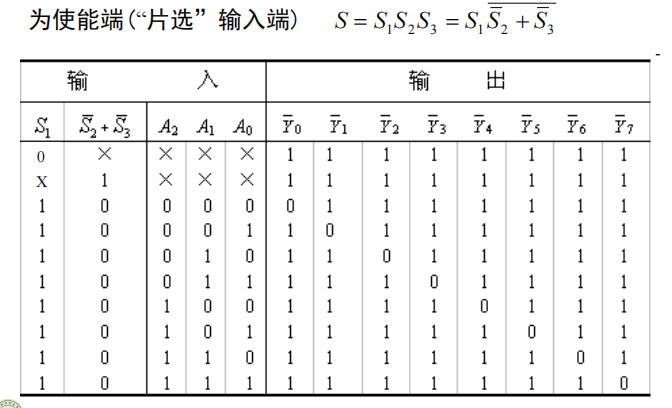
数据分配器:将一路输入数据根据地址选择码分配给多路数据输出中的某一路
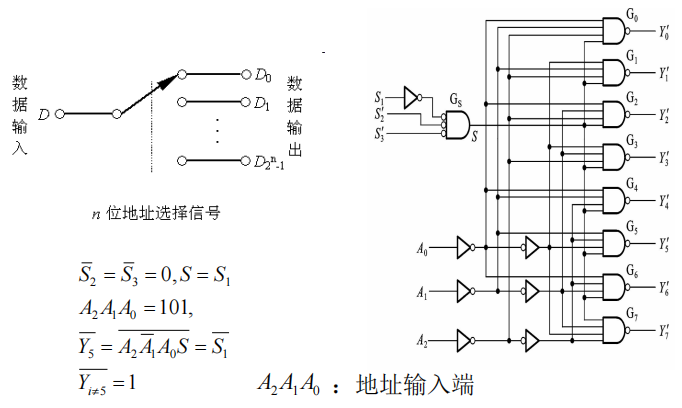
将两片74HC138扩展为4线—16线译码器:
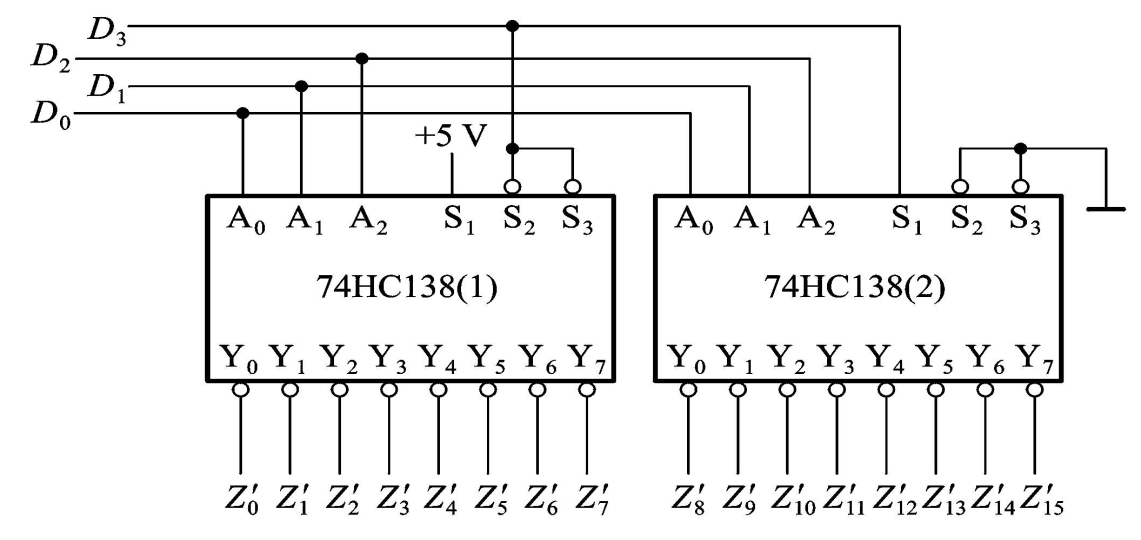
用译码器设计组合逻辑电路:

74HC42是常用的8421BCD译码器 4线—10线译码器:
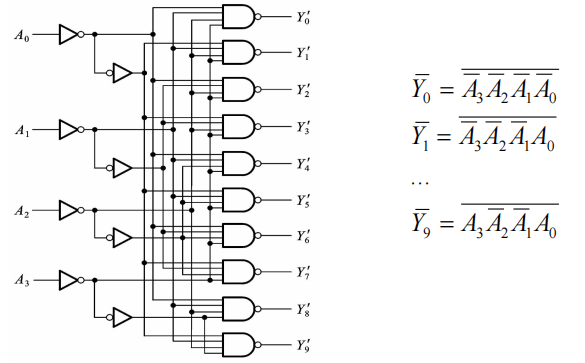
显示译码器:
能够显示数字、字母或符号的器件称为数字显示器
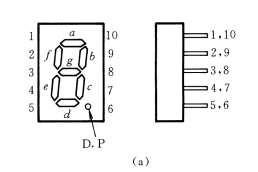
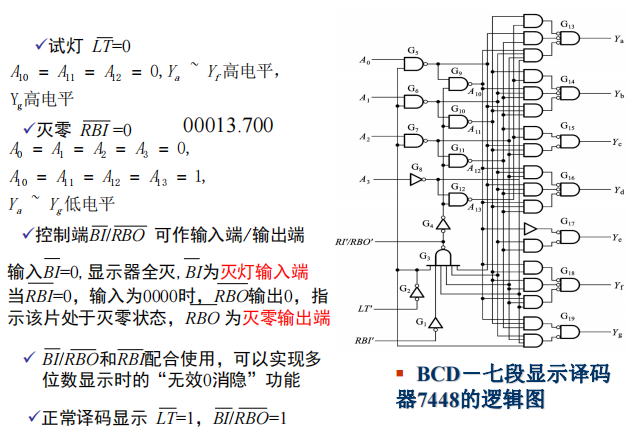
七段显示译码器7448:
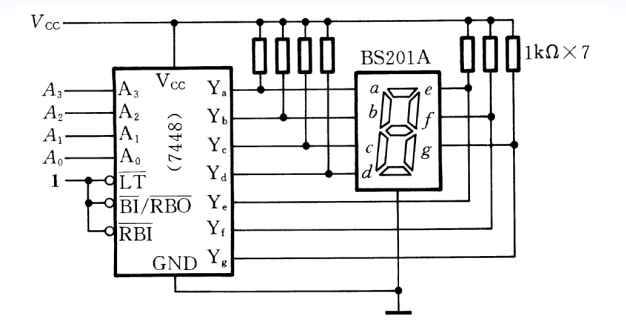
用7448驱动BS201:
数据选择器(Data Selector):
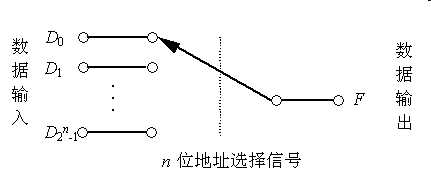
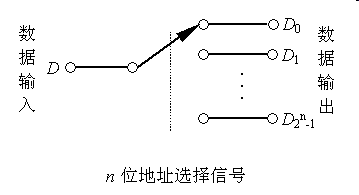
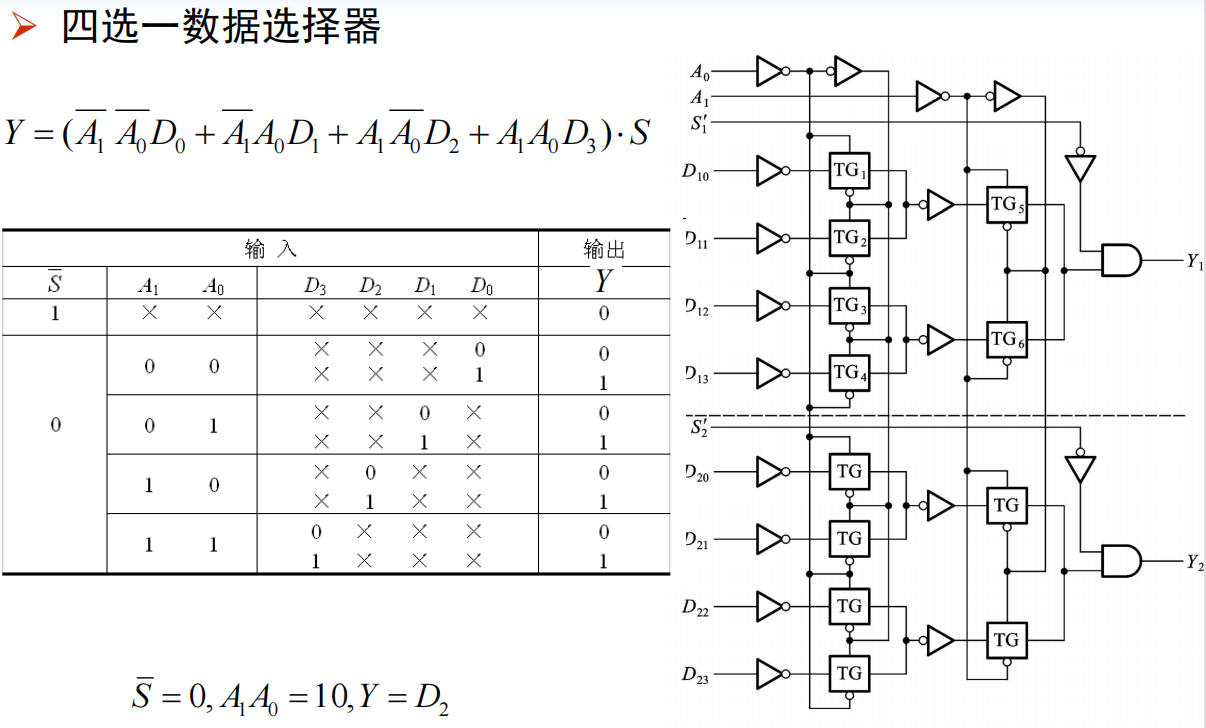
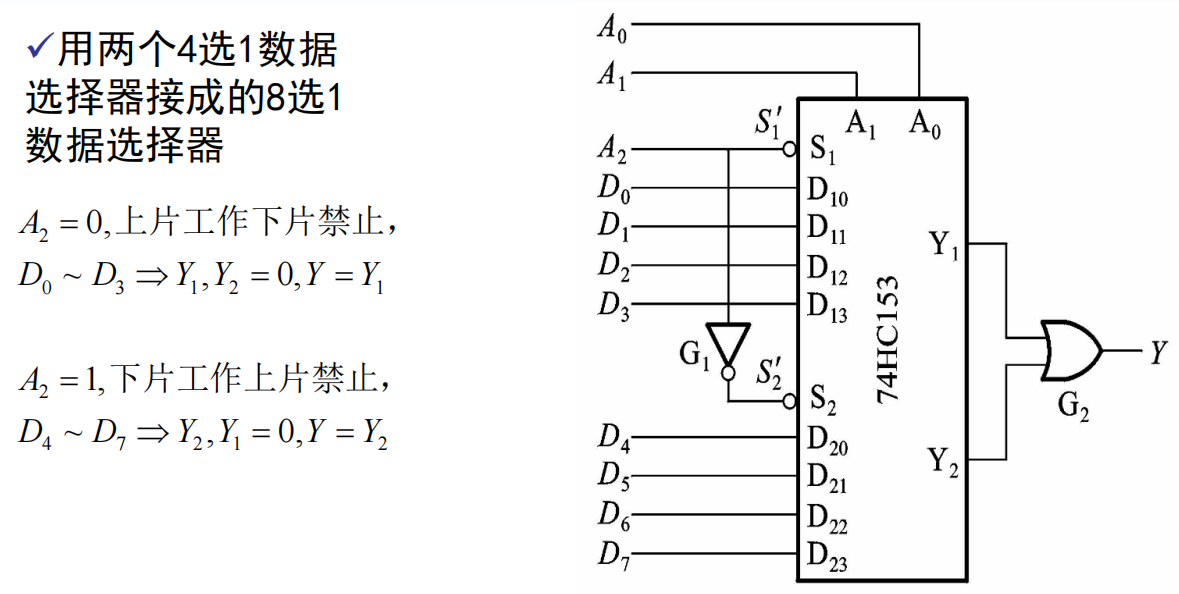
具有n位地址输入的数据选择器,可以产生任何形式输入变量数不大于n+1的组合逻辑函数
逻辑函数的变量个数(n个)等于地址输入变量个数n,用地址输入端表示输入变量
逻辑函数的变量个数(n+1个)多于地址输入变量个数n,用地址输入端表示n个输入变量,数据输入端表示另一输入变量
逻辑函数的变量个数(n+1个)多于地址输入变量个数n,用地址输入端表示n个输入变量,使能输入端表示另一输入变量(只能用于某一输入变量有一种取值对应于输出变量某一确定取值)
加法器:
1位加法器:
半加器:不考虑来自低位的进位,将两个1位的二进制数相加
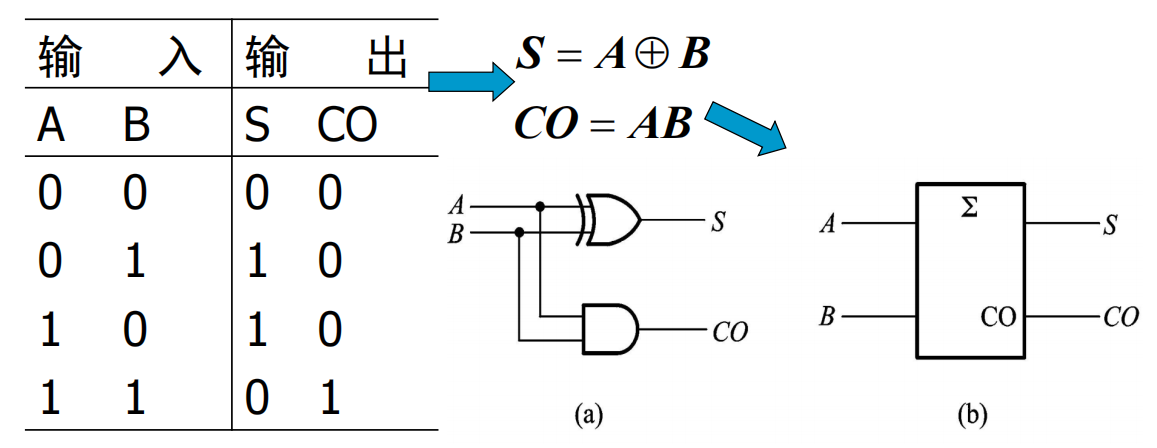
全加器:将两个1位二进制数及来自低位的进位相加
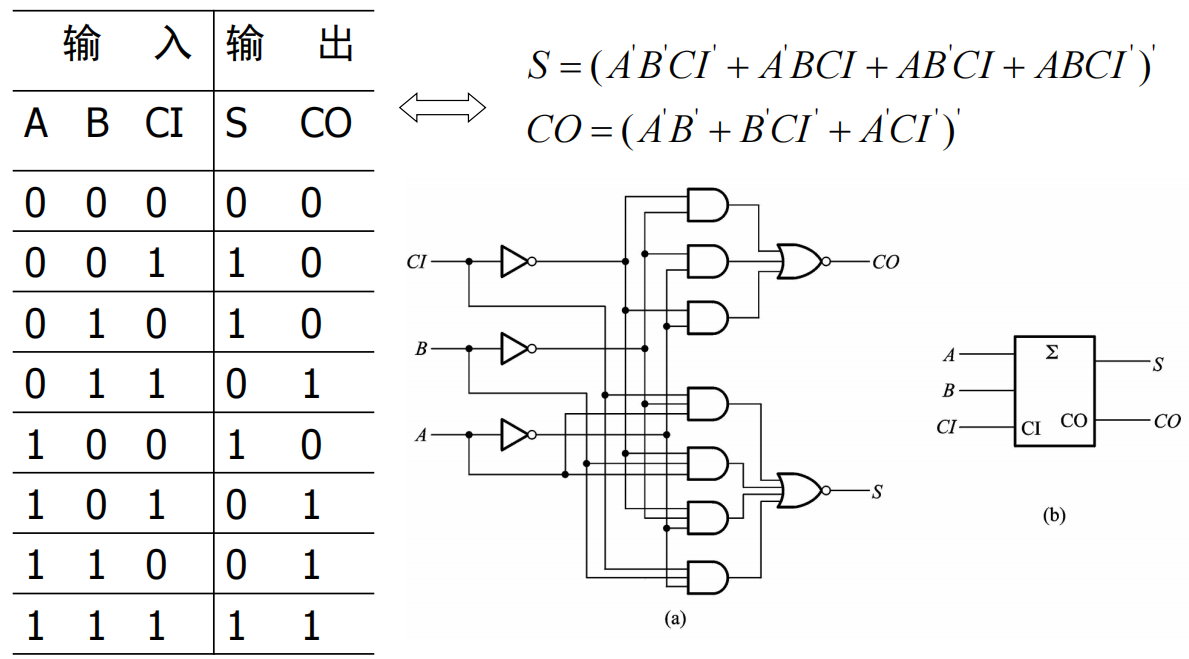
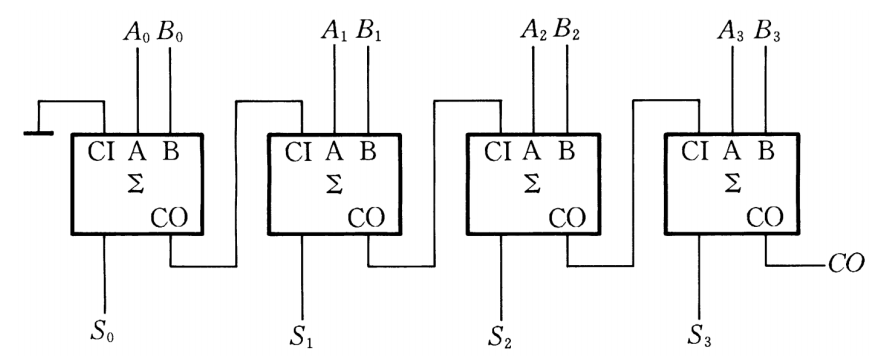
多位加法器:
串行进位加法器:优点:简单。缺点:慢
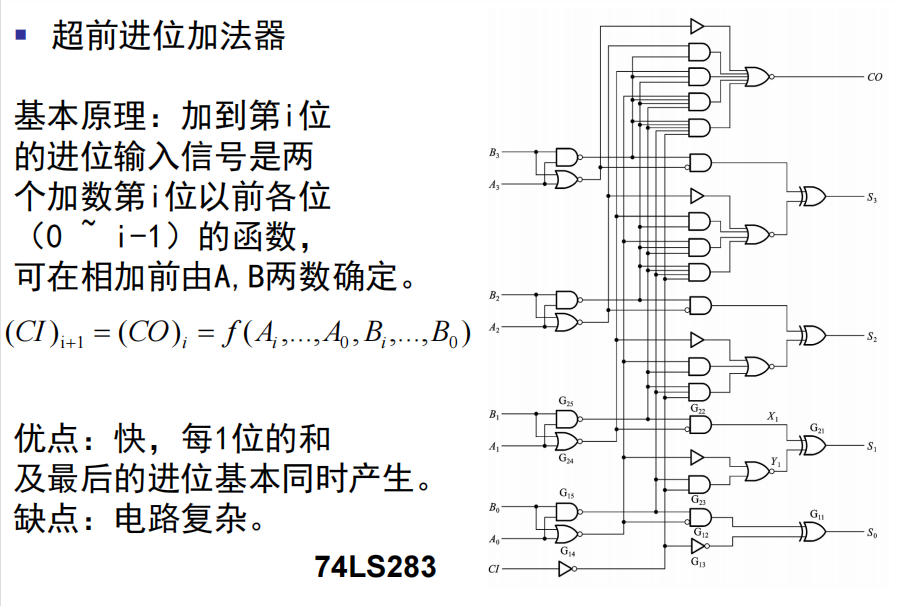
超前进位加法器:优点:快,每1位的和及最后的进位基本同时产生。缺点:电路复杂
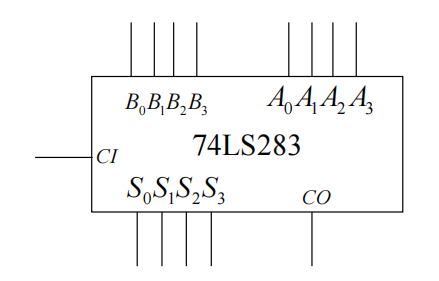
用加法器设计组合电路:
基本原理:
产生的函数可变换成输入变量与输入变量相加
产生的函数可变换成输入变量与常量相加

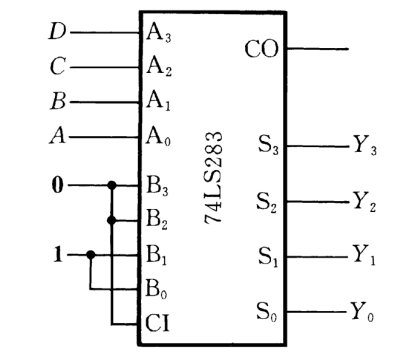
数值比较器:
对两个位数相同的二进制整数进行数值比较
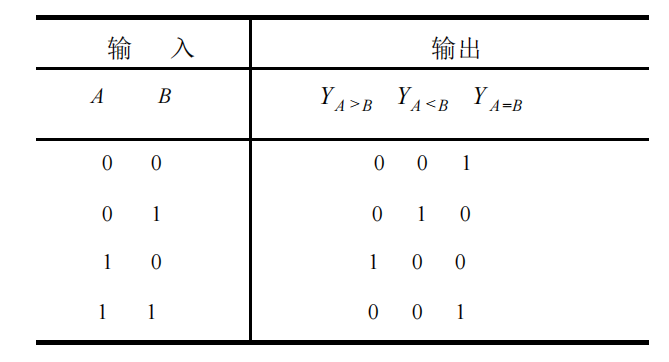
1位数值比较器:
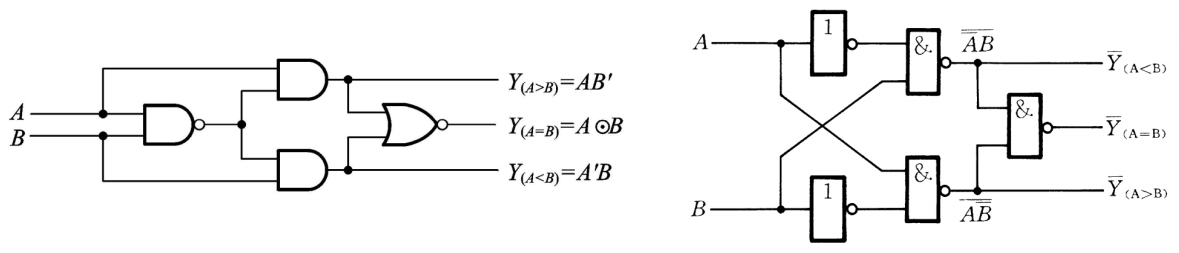
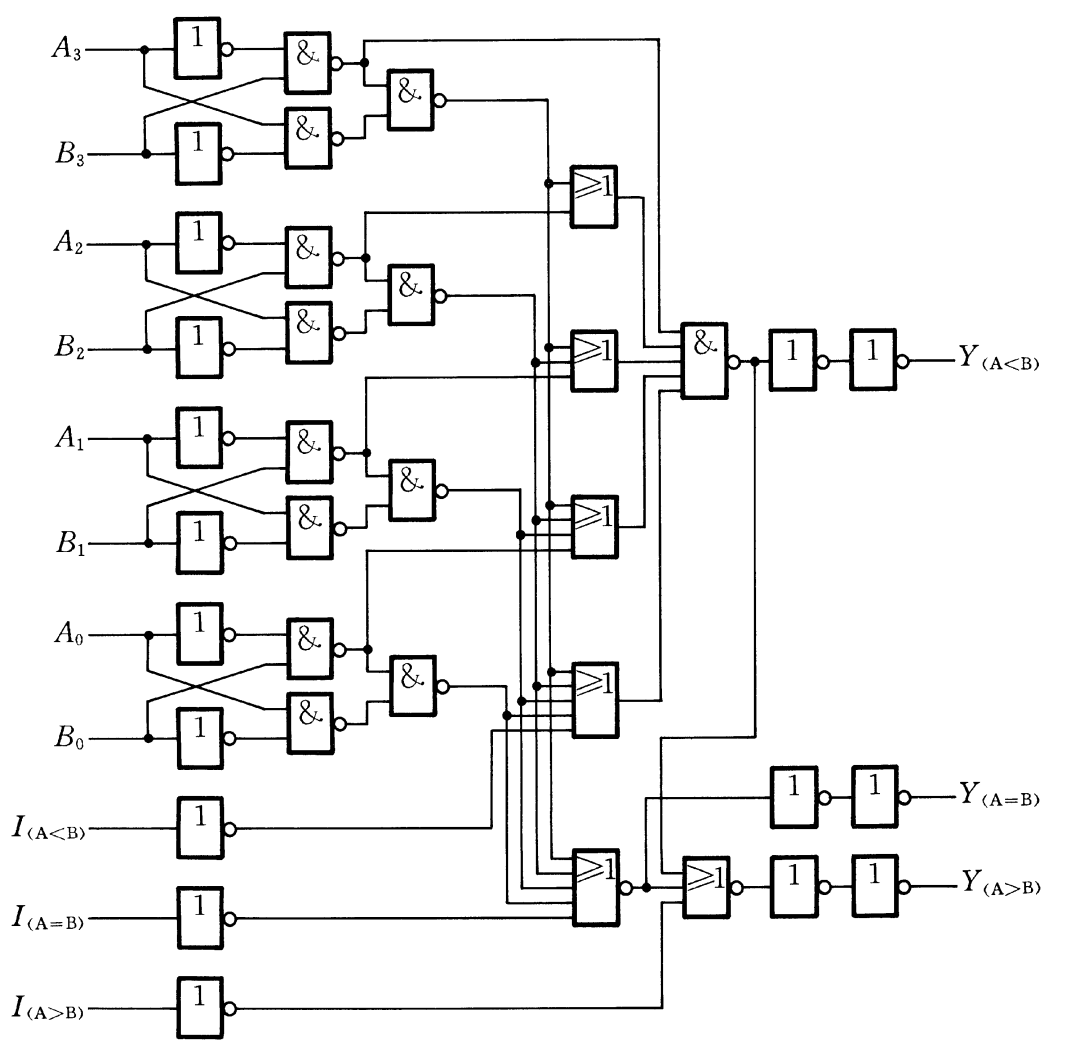
多位比较器CC14585:
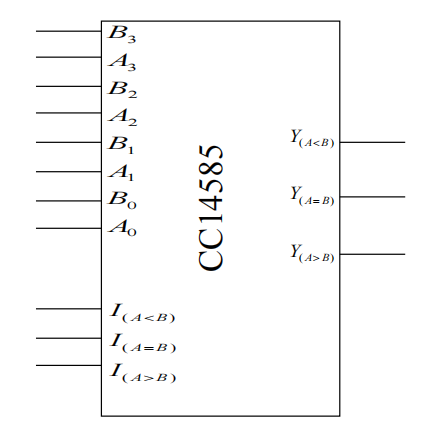
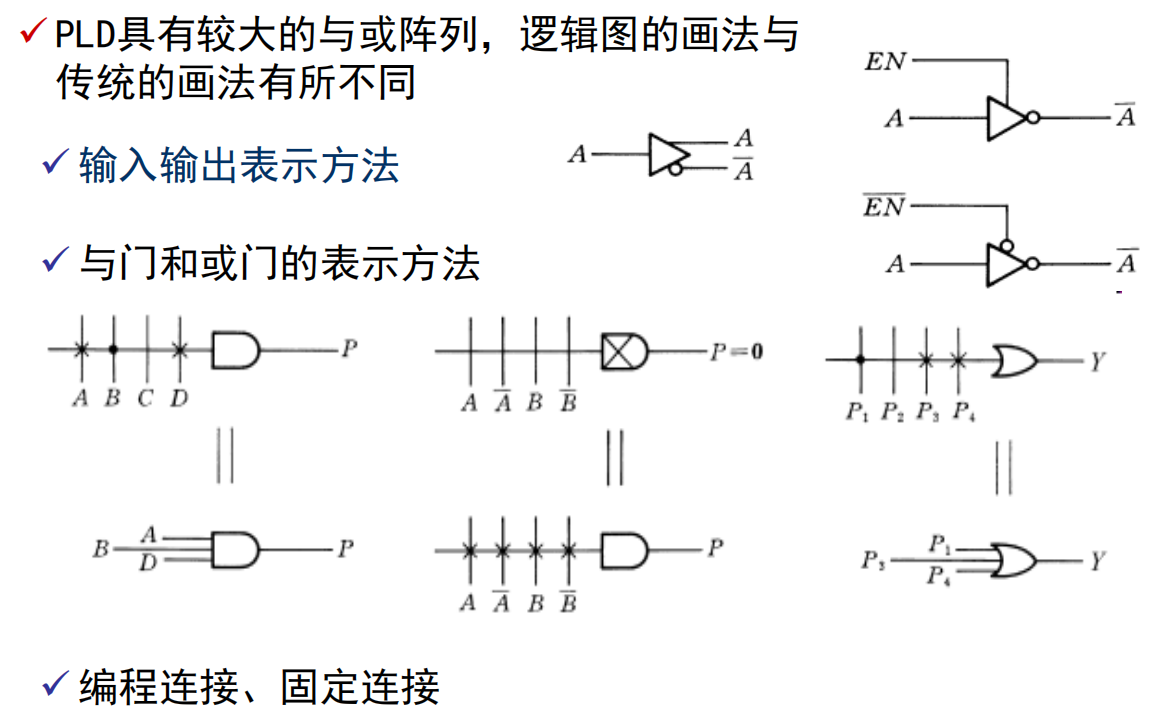
可编程逻辑器件(PLD):
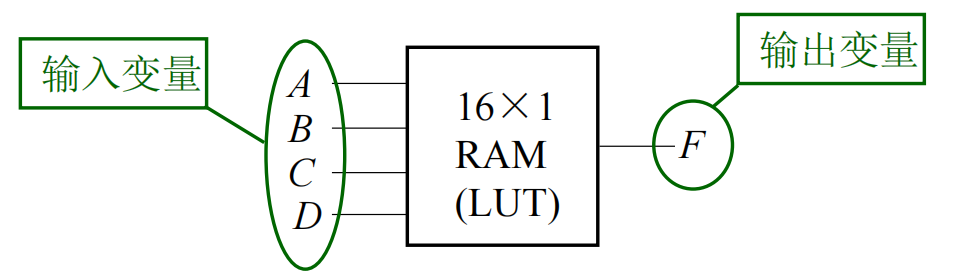
查找表结构器件:
查找表(Look Up Table)实际上是用静态存储器(SRAM)构成函数发生器
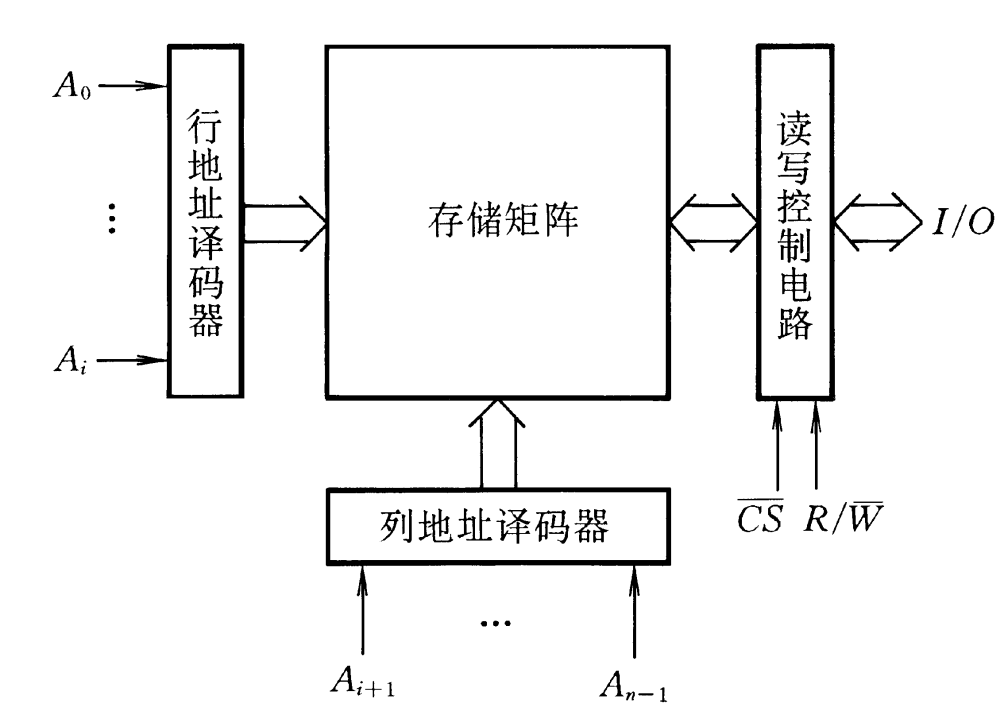
半导体存储电路
存储电路:存储数字系统工作时的数据和信息
存储单元:存储一位二值信息的基本单元电路;分为静态存储单元和动态存储单元;静态存储单元包括锁存器和触发器
寄存器(Register):存储一组数据的存储电路,由触发器组成,每个触发器的输入端输出端都被直接引出,便于快速数据交换
存储器(Memory):存储大量数据的存储电路,采用寻址读/写工作方式;分为随机存储器(Random Access Memory,RAM)和只读存储器(Read-Only Memory,ROM)
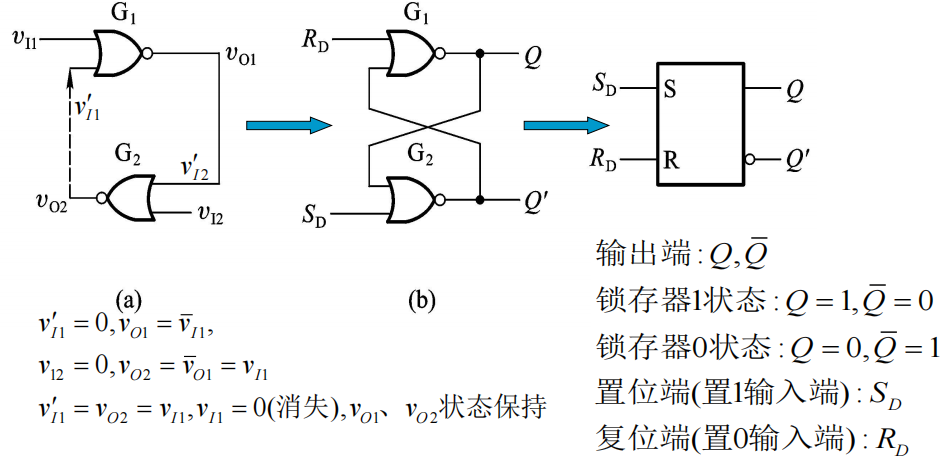
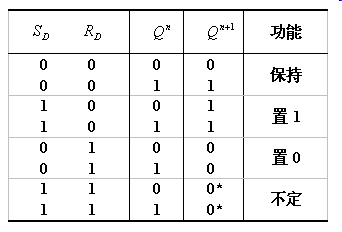
SR锁存器(Set-Reset Latch):
在任何时刻,输入都能直接改变输出的状态
用或非门组成的锁存器
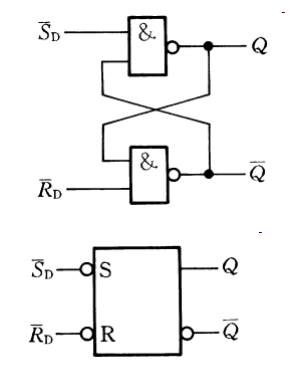
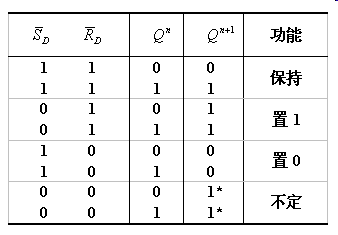
用与非门组成的锁存器
触发器(Flip-Flop):
• 相比锁存器增加了触发信号输入端
• 只有触发信号到达时,置1、置0信号才能改变触发器状态
• 触发方式分为电平、边沿、脉冲
• 不同的触发方式下触发器动作特点不同
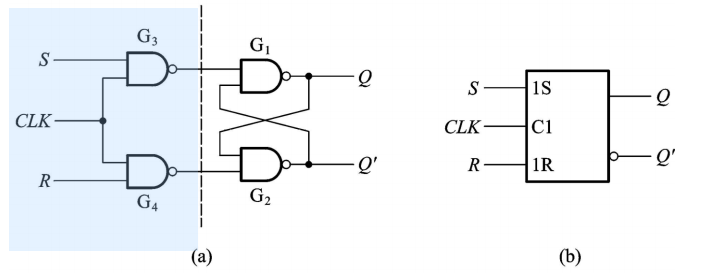
• SR锁存器+输入控制电路
• 只有触发信号CLK到达,S和R才起作用
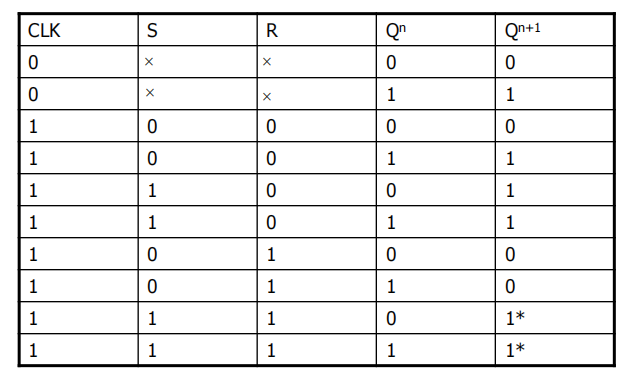
• 只有CLK为有效电平时,触发器才能接受输入信号并改变成相应状态
• 在CLK=1的全部时间里,S和R的变化都将引起输出状态的变化; CLK回到0后,触发器保存的是CLK回到0前瞬间的状态
边沿触发的触发器(edge-triggered) :
边沿触发器的动作特点:
• 触发器的次态仅取决于CP信号的上升沿(或下降沿)到达时输入的逻辑状态,与在此前、后输入的状态没有关系
• 增强了触发器的抗干扰能力,提高了电路的工作可靠性
SR脉冲触发触发器:
脉冲触发SR触发器(主从SR触发器):
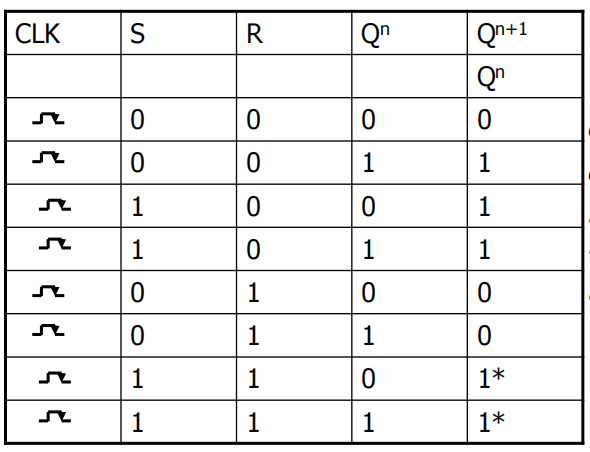
clk = 1时,“主”按 翻转,“从”保持
clk 下降沿到达时,“主”保持,“从”根据“主”的状态翻转,所以每个 周期,输出状态只可能改变一次
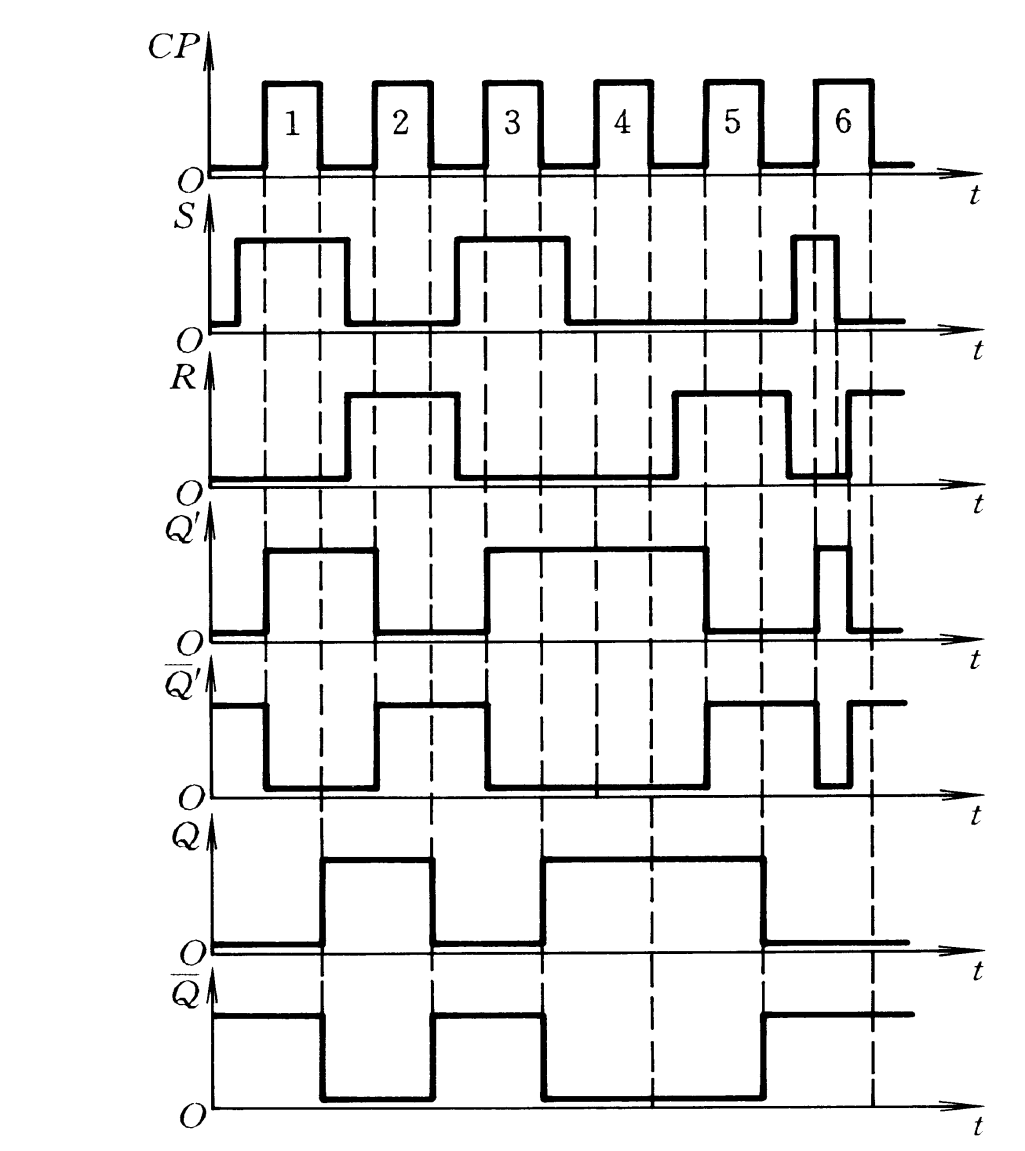
JK脉冲触发触发器:
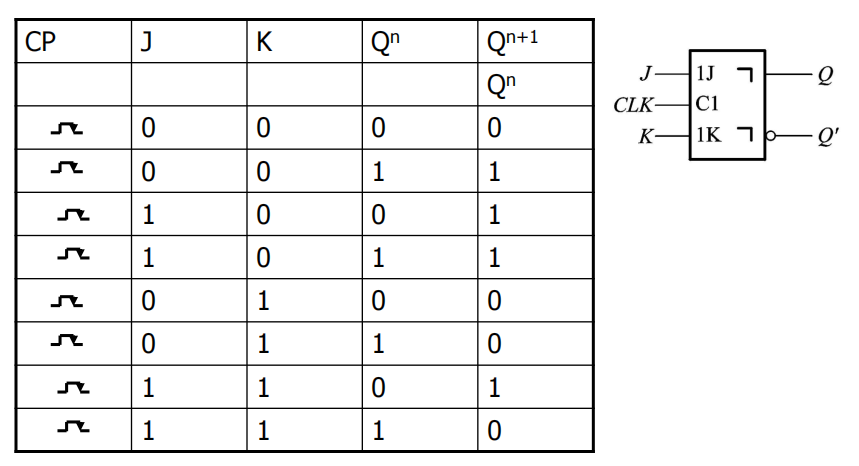
一次变现象
CLK=1期间主触发器只能翻转一次,因为
Q^n^=0 时,主触发器只能接受置1信号
Q^n^=1 时,主触发器只能接受置0信号
T触发器:
将JK触发器的的两个输入端连在一起作为T端
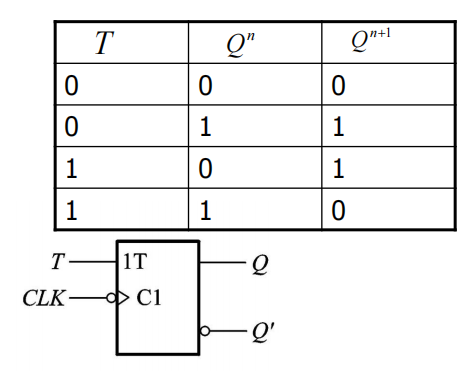
D触发器:
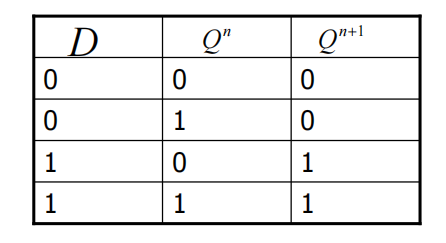
触发器功能转换:
定型产品只有JK触发器和D触发器
JK触发器转换为其他触发器:
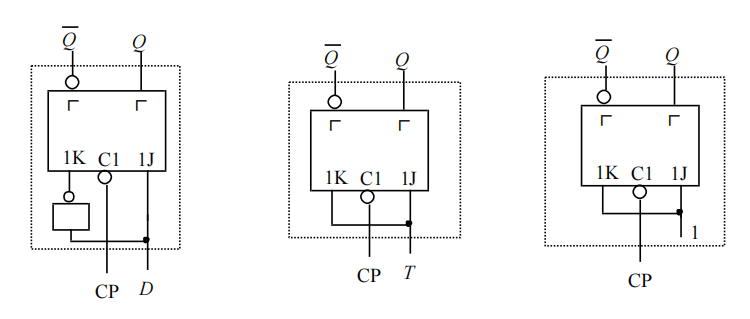
D触发器转换为其他触发器:
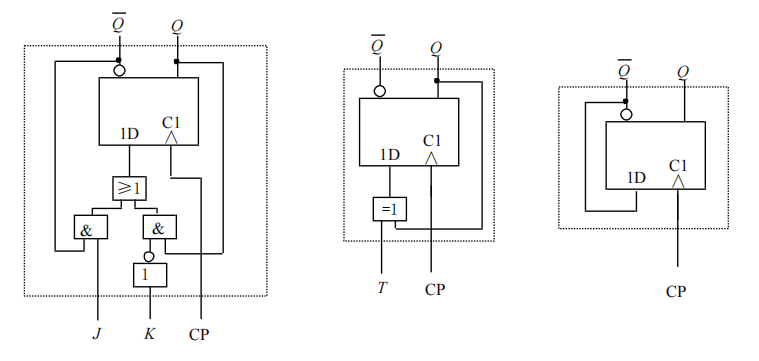
寄存器(Register):
能够寄存一组二值代码
用n个触发器就可以存储n位二进制数
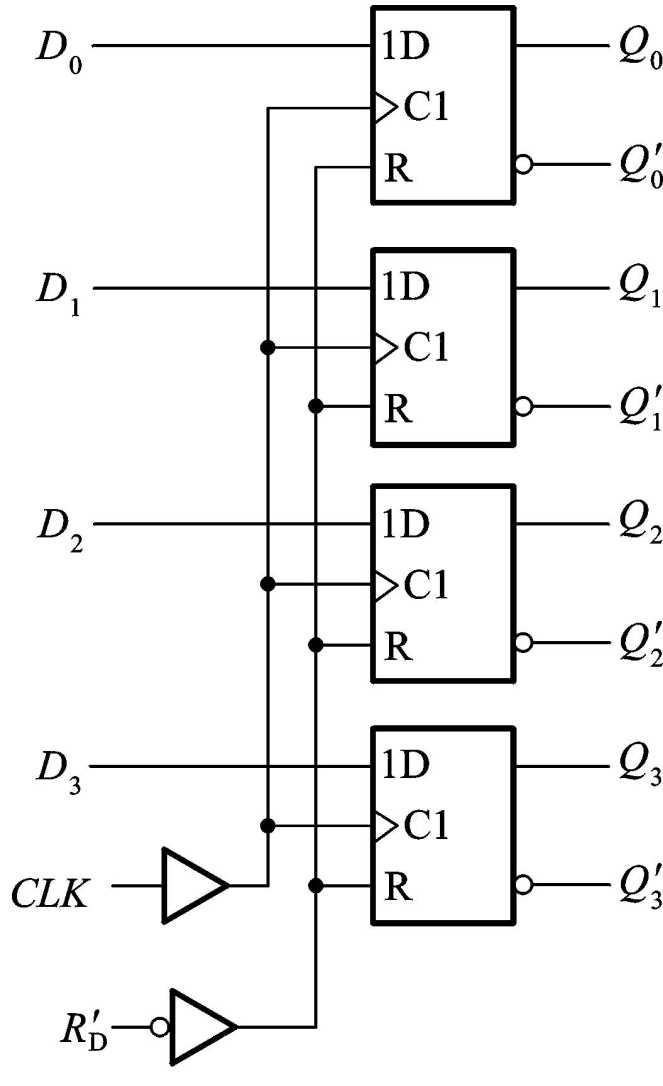
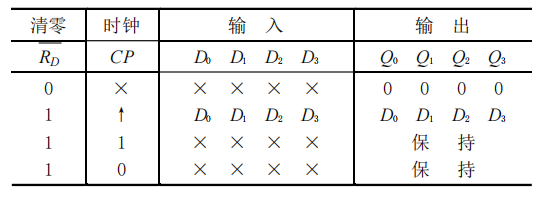
静态随机存储器(SRAM):