好的，这份讲座PPT（由新加坡国立大学的Xudong CHEN教授在清华大学发表）深入探讨了物理学如何指导机器学习在波传感与成像领域的应用。其核心思想是，纯粹的“黑箱”机器学习方法在该领域存在严重局限，而“物理辅助”的机器学习方法则能有效克服这些局限，取得卓越成果。

以下是我对讲座中关于机器学习功能、作用和局限性的总结，并在此基础上展开详细说明。

核心总结

1. 机器学习的局限性（黑箱方法的困境）：
讲座指出，在处理复杂的波物理问题时，直接套用在计算机视觉等领域大获成功的“黑箱”深度学习模型，往往会失败。其核心局限在于：

  • 泛化能力差（唯一性问题）： 模型可以完美拟合有限的训练数据，但由于没有学到数据背后真正的物理规律，导致其在面对训练集以外的数据时表现很差。物理问题的解通常是唯一的，而黑箱模型仅凭数据拟合可能找到无数个“伪解”。
  • 效率低下且浪费知识： 强迫神经网络从零开始学习已经被人类研究了数十年的、有明确数学表达式的物理定律（如波动方程、格林函数等），是极其低效且不必要的。这相当于丢弃了宝贵的先验知识。

2. 机器学习的功能（作为“增强器”与“校正器”）：
讲座倡导的“物理辅助”方法，重新定义了机器学习的功能。在这里，机器学习不再是一个端到端的“万能求解器”，而是扮演以下角色：

  • 物理模型的“校正器”： 首先使用一个快速但不够精确的传统物理模型（如基于傅里叶变换的算法）得出一个初步结果。这个结果可能包含伪影或误差。然后，让神经网络来学习并校正这个初步结果与真实结果之间的“误差”或“残差”。
  • 复杂关系的“建模器”： 在物理模型难以精确描述或计算成本过高的部分，利用机器学习强大的非线性拟合能力来建模。

3. 机器学习的作用（从图像增强到智能分类）：
在这种新范式下，机器学习的具体作用体现在：

  • 图像重建与增强： 在成像问题中，神经网络（如U-Net）的输入不再是原始传感数据，而是经过物理模型（如远场近似FFA）初步处理后的图像。神经网络的任务是将这张“粗糙”的图像变得“清晰”，去除伪影。
  • 物理特征的智能分类： 在分类问题（如雷达目标识别）中，首先利用物理公式从原始信号中提取出具有明确物理意义的特征（如速度、总反射率、面积、入射角等）。然后，将这些高度浓缩的、信息量大的特征输入到一个简单的神经网络（如MLP）中进行分类。

详细展开说明

一、 机器学习的局限性：黑箱方法的困境

讲座通过多个层面论证了为什么不能简单地将机器学习视为一个“黑箱”。

  • 问题复杂度的根本差异（Slide 5）：

    • 计算机视觉（CV）： 物理规律相对简单（如基于短波长的傅里叶光学），问题本身在数学上不那么复杂。
    • 波传感与成像（WS/WI）： 物理规律通常很复杂（如麦克斯韦方程），问题在数学上本身就非常复杂和“病态”（ill-posed），无论是否使用机器学习，其求解难度都很大。

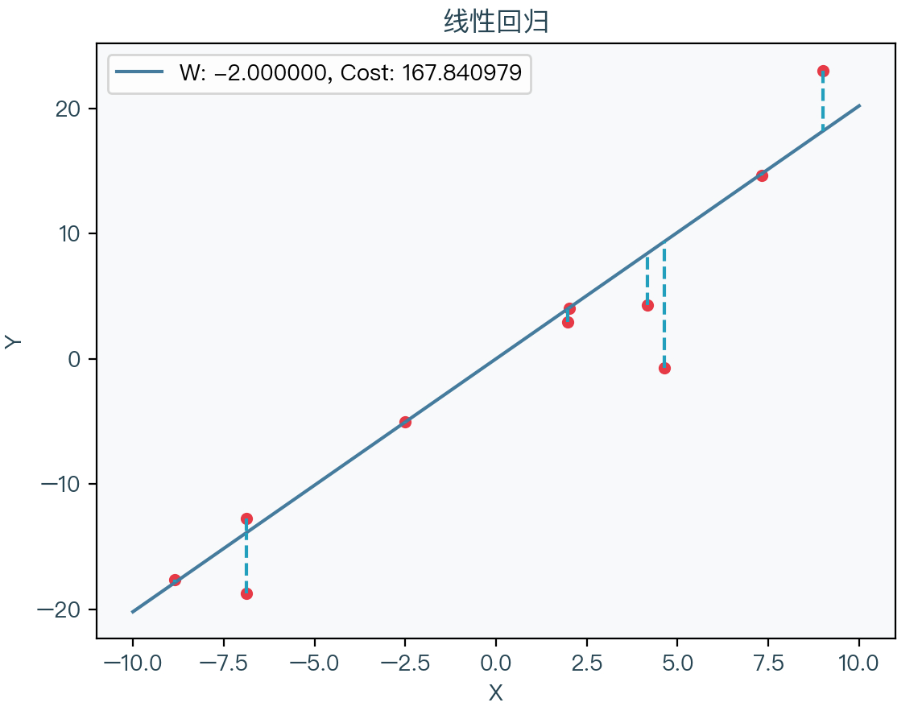
  • 致命的“唯一性问题”（Uniqueness Problem, Slides 6-7）：
    这是讲座中最核心的论点之一。讲座用一个绝佳的数学例子说明了这个问题：

    • 问题： 已知 f(1)=1, f(2)=4, f(3)=9, f(4)=16, f(5)=25，求 f(6) 是多少？
    • 直观答案： f(6) = 36，因为我们识别出了物理规律 f(n) = n²。
    • 黑箱模型的“陷阱”： 一个黑箱模型可能会找到另一个完全不同的函数，例如 f(n) = n² + (n-1)(n-2)(n-3)(n-4)(n-5)g(n)，其中 g(n) 是任意函数。这个函数对于 n=1 到 5 的所有训练数据，其结果都完美等于 n²，因为第二项始终为零。但对于 n=6，其预测值 f(6) = 36 + 120 * g(6)，结果完全取决于任意的 g(6)，因此预测是不可靠的。
    • 结论： 对于波成像这类逆问题，黑箱神经网络总能完美拟合训练数据，但由于没有被物理定律所约束，它无法保证在面对新数据时具有良好的泛化能力。因此，必须引入物理学，即波动方程的知识，来约束解空间，保证解的唯一性和稳定性。

二、 机器学习的功能：作为物理模型的“增强器”和“校正器”

讲座提出的解决方案是“物理辅助学习”，核心是“分工合作”：让人类擅长的部分（逻辑清晰的物理建模）和机器擅长的部分（处理复杂非线性关系）各司其职。

  • 简化神经网络的任务（Slide 9, 22）：
    • 黑箱方式： 任务难度是固定的，神经网络需要从头学习从 原始数据y 到 目标参数x 的极其复杂的反演关系。
    • 物理辅助方式： 我们的目标是设计一个更简单的输入-输出关系。我们不直接学习 x = G(y)，而是先用一个简单的物理模型 x_approx = F(y) 得到一个近似解，然后让神经网络学习 x = NN(x_approx) 这个修正过程。
    • 核心功能（Slide 22）： 讲座用一张图清晰地说明：对于一个本该用线性方程求解器解决的问题，我们先用一个更快的FFT-based求解器得到一个有误差的结果，然后让神经网络去学习并修正这个FFT结果的误差。神经网络的功能是“学习一个物理模型的误差”。

三、 机器学习的作用：具体应用案例

讲座通过两个主要案例展示了这种思想的强大威力。

  • 案例一：远场近似学习方法（FFALM）用于成像（Slides 14-21）

    • 传统方法 vs. 黑箱方法： 传统方法需要求解复杂的积分方程，计算量大；黑箱方法直接将测量数据输入神经网络，如前所述，泛化能力差。
    • 物理辅助方法（FFALM）：
      1. 输入端改造 (Input)： 不将原始测量数据 E_s 直接送入网络，而是先应用一个基于“远场近似”物理模型的逆傅里叶变换，得到一个初步的、带有伪影的图像 f_1（Slide 14）。这个操作将复杂的物理反演问题，转换为了一个“图像去噪/图像修复”问题。
      2. 标签端改造 (Label)： 输出的标签不使用理想但难以学习的“狄拉克函数”（delta function），而是使用更平滑、更符合物理实际的“点扩散函数”（PSF）（Slide 15）。
      3. 网络作用： U-Net（一种常用于图像到图像转换的网络）的作用就是将输入的这张“粗糙”的图像，处理成高质量、无伪影的最终图像。实验结果（Slides 18-21）表明，无论是在模拟还是真实实验数据上，这种方法都取得了优异的重建效果。

  • 案例二：77GHz雷达目标分类（Slides 32-37）

    • 黑箱方法（Black-box CNN, Slide 36）： 将雷达生成的“距离-多普勒（R-D）图”作为一张二维图像，直接输入到卷积神经网络（CNN）中进行分类。这需要一个大型网络（如2500个输入节点），且网络需要自己从像素点中发现目标类别（行人、自行车、轿车等）的规律。
    • 物理辅助方法（Proposed Method, Slides 34-35）：
      1. 物理特征提取： 利用明确的波动物理学公式，从原始信号中计算出四个关键物理特征：速度（Velocity）、总反射率（ToRe）、散射面积（Area）、入射角（Incidence angle）。
      2. 网络作用： 将这4个高度凝练的特征值输入到一个非常简单的多层感知机（MLP）中。此时，神经网络的作用不再是“看图”，而是基于物理意义明确的几个数值进行“决策”。
    • 结果对比（Slide 37）： 结果天差地别。物理辅助方法的分类准确率极高（如行人、自行车、轿车识别率100%），而黑箱CNN方法则出现了严重的混淆（如将38%的自行车误识别为轿车）。这雄辩地证明了，为神经网络提供具有清晰物理意义的输入，远比让它在原始数据中盲目探索要高效和准确得多。

总而言之，该讲座的核心信息是，在科学与工程领域应用机器学习，不能盲目崇拜“端到端”的黑箱模型。最高效、最稳健的方法是将领域知识（物理学）与机器学习的优势相结合，通过物理模型简化和规范问题，让机器学习去完成那些传统方法难以处理的、复杂的、非线性的“最后一公里”任务，最终实现“1+1>2”的效果。