This is an excellent collection of articles for analysis, as they are from a cohesive research area (and often the same research group), showcasing a clear and consistent style for writing high-impact scientific papers in computational science and engineering.

Based on an analysis of the provided textbook chapter and research articles, here is a summary of their writing characteristics and a guide on the train of thought for composing a similar article.

Overall Train of Thought

The core logic follows a “funnel” structure, moving from a general problem to a specific solution and then back to general implications.

  1. Problem: What is the broad, important problem we are trying to solve? (e.g., Inverse Scattering Problems).
  2. Challenge: Why is this problem hard? What specific aspect makes it difficult? (e.g., It’s ill-posed, nonlinear, and becomes even harder with phaseless data).
  3. State of the Art: How have others tried to solve this? What are the existing methods and what are their limitations? (e.g., Traditional iterative methods are slow; early deep learning methods are “black boxes”).
  4. Our Idea (The Gap): We have a novel idea to overcome a specific limitation. (e.g., “We can inspire the neural network design with physics” or “We can quantify the uncertainty of the deep learning prediction”).
  5. Our Method (The Solution): This is exactly how our idea is implemented, mathematically and algorithmically.
  6. Proof: How do we prove our method works and is better than the state of the art? (e.g., Through carefully designed numerical experiments and quantitative metrics).
  7. Implications: What is the significance of our work? Why does it matter and what’s next? (e.g., Our method is faster, more accurate for challenging cases, and opens up new research directions).

Breakdown by Section

Here is how this train of thought is structured in each part of the paper.

1. Abstract

The abstract is a highly condensed version of the entire paper, following a strict formula.

  • Starts with: A single sentence establishing the context and the primary challenge.
    • Example: “Reconstructing the exact electromagnetic property of unknown targets from the measured scattered field is challenging due to the intrinsic nonlinearity and ill-posedness.”
  • The “Gap” and “Our Proposal”: Immediately state what is missing and what you are proposing to fix it.
    • Example: “In this article, a new scheme, named the modified contrast scheme (MCS), is proposed to tackle nonlinear inverse scattering problems (ISPs).”
  • Core Technical Idea: Briefly state the key mechanism of your method.
    • Example: “A local-wave amplifier coefficient is used to form the modified contrast, which is able to alleviate the global nonlinearity…”
  • Key Result & Validation: Summarize the main finding from your experiments.
    • Example: “The numerical results show that MCS with the modified contrast input performs well in both 2-D and 3-D testing examples…”
  • Concluding Impact: A final sentence on why this is a significant improvement.
    • Example: “…a significant improvement is achieved in reconstructing high-contrast scatterers.”

2. Introduction

The introduction expands the abstract into a full narrative that guides the reader from the general field to your specific contribution.

  • Starts with (The Broad Funnel Opening): A broad statement about the importance and application of the field.
    • Example: “Electromagnetic inverse scattering problems (ISPs) are aimed at determining the nature of unknown scatterer… and have wide applications in the fields of nondestructive evaluation, geophysics, biomedical imaging…”
  • Defining the Challenge: Explain in more detail why the problem is difficult (nonlinearity, ill-posedness, computational cost, challenges of phaseless data). This educates the reader and sets the stage for why new methods are needed.
  • Literature Review (State of the Art): Systematically review existing categories of solutions.
    • Start with traditional methods (e.g., iterative solvers like DBIM, CSI, SOM) and state their pros and cons (e.g., physically grounded but slow).
    • Move to more recent approaches (e.g., early machine learning, deep learning) and state their pros and cons (e.g., fast but often “black boxes” lacking generalization).
  • Identifying the Specific Gap: Explicitly state the limitation in the state-of-the-art that your work will address. This is the most crucial part of the introduction.
    • Example: “However, little attention has been paid to the uncertainty quantification of these deep-learning methods…” or “In [29], the similarities between the iterative method… and the architecture of ANN have also been examined, which inspires to propose…”
  • Stating Your Contribution (The “Here We Show” Moment): Clearly and concisely list your paper’s contributions. Use a bulleted or numbered list for maximum clarity.
    • Example: “The main contributions of the proposed method are threefold. First… Second… Third…”
  • Paper Roadmap: End with a brief outline of the rest of the paper.
    • Example: “The structure of this article is as follows. Section II presents the formulation… Section III shows the numerical comparison…”

3. Methods (Formulation / Methodology)

This section is the technical core. The goal is precision and clarity, allowing another expert to understand and replicate your work.

  • Starts with the Foundation: Begin with the established physics and mathematical model (e.g., the Lippmann–Schwinger equation, the state and data equations). Define all terms, variables, and operators.
    • Example: “In ISPs, the forward model can be formulated by the following two discretized equations…”
  • Connecting to Your Idea: Bridge the foundational theory to your novel concept. Explain the high-level idea before diving into the mathematical details.
    • Example: “Inspired by contrast-source type iterative inversion solvers… we turn our attention from directly regressing contrast to the problem of estimating induced current…”
  • Detailing the Novelty: Provide a step-by-step derivation of your method. Use equations, algorithms (in pseudo-code), and diagrams (especially for neural network architectures). Justify your design choices.
    • Example: When describing a new input for a neural network, explain why that input is physically meaningful and more suitable than previous approaches (e.g., “The new constant value β₀ for the input generation provides us a freedom to control the performance of the U-Net.”).
  • Final Output Formulation: Clearly state how the final result (e.g., the reconstructed image) is obtained from your method’s output.

4. Numerical Results / Experiments

This section provides the evidence. The structure is methodical and focused on comparing your method against relevant benchmarks.

  • Starts with the Setup: Describe the simulation or experiment configuration in detail. This is critical for reproducibility.
    • Example: “In the numerical tests, we consider a DOI D with the size of 2 × 2 m² and discretize the domain into 64 × 64 pixels. The operating frequency is 400 MHz…”
    • Specify training/testing data, noise levels, and the quantitative metrics you will use (e.g., Relative Error, SSIM).
  • Present Results by Case Study: Organize the results into distinct examples or tests. Each test should be designed to prove a specific point (e.g., performance on weak scatterers, performance on strong scatterers, generalization ability, robustness to noise).
  • Show, Don’t Just Tell: Use figures (reconstructed images) and tables (quantitative scores) extensively. The figures should always include the “Ground Truth” for visual comparison.
  • Interpret the Results: For each figure and table, add text that guides the reader’s interpretation.
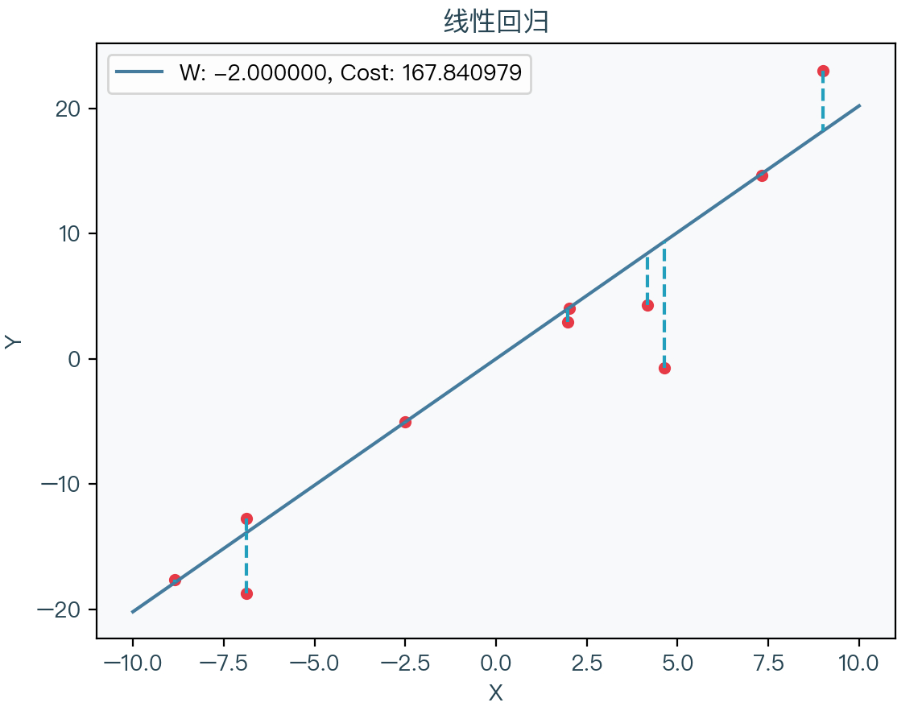
    • Example: “As demonstrated in Fig. 5(c) and (d), some artifacts appear in the reconstruction… while MCSM still offers a satisfactory reconstruction result. The average Re… is listed in Table II.”

5. Discussion and Conclusion

This section zooms back out. It summarizes the work and explains its broader significance.

  • Starts with a Restatement: Begin by restating the problem and your proposed solution in a single paragraph.
    • Example: “In this article, an improved scheme, named MCS, is proposed to tackle nonlinear ISPs. Under the MCS, both 2-D and 3-D real-time reconstruction results are provided…”
  • Summarize Key Findings: Briefly reiterate the most important results and what they prove.
    • Example: “It is found that, although the network is trained with MNIST data set, it is able to solve general ISPs and outperforms SOM and DCS in reconstructing some challenging profiles.”
  • Discuss the “Why”: Explain why your method performed well. Connect the successful results back to the design features you described in the Methods section. This provides deeper insight.
    • Example: “One reason for the better performance of MCSM is that the range of the modified contrast is always between 0 and 1, which makes it more suitable to be the input of the U-Net.”
  • Acknowledge Limitations and Propose Future Work: Show that you have a critical understanding of your own work by mentioning its limitations and suggesting how the research could be extended in the future.
    • Example: “Although the proposed method quantitatively achieves significantly better results… there is still room for improvements considering the advantages that have been exhibited by some iterative algorithms that are specially designed to tackle highly nonlinear ISPs…”

By following this structured train of thought, you can create a clear, logical, and persuasive scientific article that effectively communicates your contribution to the field.

Abstract

Far-Field Approximation Learning Method for Millimeter-Wave Short-Range Imaging

一种毫米波短距离成像的远场近似学习方法

1
2
3
Abstract — Based on the far-field approximations, a deep learning-based method is proposed for millimeter-wave shortrange imaging. By using convolutional neural networks, the distortions caused by the far-field approximations and limitedaperture measurements could be corrected. Dissimilar to traditional algorithms, the proposed method has no restrictions on the placements of the antenna arrays and single-frequency illuminations are sufficient for the generations of 3-D highresolution reflectivity maps. In addition, it is fast to generate the input of neural network since the algorithm is based on inverse Fourier transform, which is ideal for generating training dataset. The performance of the proposed method is verified using both synthetic and experimental data. It is also demonstrated that enlarging the k-space coverage, which can be accomplished by increasing the dimensions of the antenna arrays, can improve the resolution of the proposed method.

摘要——基于远场近似，提出了一种基于深度学习的毫米波短程成像方法。通过使用卷积神经网络，可以校正由远场近似和有限扰动测量引起的失真。与传统算法不同，该方法对天线阵列的放置没有限制，单频照明足以生成三维高分辨率反射率图。此外，由于该算法基于傅里叶逆变换，因此生成神经网络的输入很快，非常适合生成训练数据集。使用合成数据和实验数据验证了所提出方法的性能。还证明了通过增加天线阵列的尺寸来扩大k空间覆盖范围可以提高所提出方法的分辨率。

An Improved Deep Learning Scheme for Solving 2-D and 3-D Inverse Scattering Problems

一种用于求解二维和三维逆散射问题的改进深度学习方案

1
2
3
Abstract— Reconstructing the exact electromagnetic property of unknown targets from the measured scattered field is challenging due to the intrinsic nonlinearity and ill-posedness. In this article, a new scheme, named the modified contrast scheme (MCS), is proposed to tackle nonlinear inverse scattering problems (ISPs). A local-wave amplifier coefficient is used to form the modified contrast, which is able to alleviate the global nonlinearity in original ISPs without decreasing the accuracy of the problem formulation. Moreover, the modified contrast is more suitable to be the input of the deep learning scheme, due to the unity bound of the modified contrast. The numerical results show that MCS with the modified contrast input performs well in both 2-D and 3-D testing examples in real time after offline training process, even in high-relative-permittivity cases. Compared with the dominant current scheme, a significant improvement is achieved in reconstructing high-contrast scatterers.

摘要——由于固有的非线性和病态性，从测量的散射场中重建未知目标的精确电磁特性具有挑战性。本文提出了一种名为改进对比度方案（MCS）的新方案来解决非线性逆散射问题（ISP）。使用局域波放大器系数来形成修改后的对比度，这能够在不降低问题公式精度的情况下缓解原始ISP中的全局非线性。此外，由于修正对比度的统一界限，修正对比度更适合作为深度学习方案的输入。数值结果表明，在离线训练过程后，具有修改对比度输入的MCS在二维和三维测试示例中实时表现良好，即使在高相对电容率的情况下也是如此。与主流方案相比，在重建高对比度散射体方面取得了显著改进。

MUSIC Imaging and Electromagnetic Inverse Scattering of Multiple-Scattering Small Anisotropic Spheres

多散射小各向异性球体的MUSIC成像和电磁逆散射

1
2
3
Abstract—The Foldy-Lax equation is used to derive a multiple scattering model for the multiple-scattering small anisotropic spheres. By this model, if the number of the non-zero singular values of the multistatic response (MSR) matrix is smaller than the number of the antennas, the range space of the MSR matrix is found to be spanned by the background Green’s function vectors corresponding to the and components of the electric and magnetic dipoles induced in each scatterer, which indicates that the multiple signal classification (MUSIC) method could be implemented to obtain the locations of the scatterers. After estimating the positions of the scatterers, a non-iterative analytical method is proposed for retrieving the polarization strength tensors as well as the orientations of the principle axes of each scatterer. Two numerical simulations show that, the MUSIC method and the non-iterative method are efficacious for the nonlinear inverse scattering problem of determining the locations and polarization strength tensors of multiple-scattering small anisotropic spheres. Such methods could also be applied to the inversion of small isotropic spheres or extended to the inversion of small bianisotropic spheres.

摘要——利用Foldy-Lax方程推导了多散射小各向异性球体的多散射模型。通过该模型，如果多稳态响应（MSR）矩阵的非零奇异值的数量小于天线的数量，则发现MSR矩阵的距离空间由与每个散射体中感应的电偶极子和磁偶极子的分量对应的背景格林函数向量跨越，这表明可以实现多信号分类（MUSIC）方法来获得散射体的位置。在估计散射体的位置后，提出了一种非迭代分析方法来反演极化强度张量以及每个散射体主轴的方向。两个数值模拟表明，MUSIC方法和非迭代方法对于确定多散射小各向异性球体的位置和极化强度张量的非线性逆散射问题是有效的。这种方法也可以应用于小各向同性球体的反演，或扩展到小双各向异性球体的反演。

Deep Learning-Based Inversion Methods for Solving Inverse Scattering Problems With Phaseless Data

基于深度学习的求解无相位数据逆散射问题的反演方法

1
2
3
Abstract— Without phase information of the measured field data, the phaseless data inverse scattering problems (PD-ISPs) counter more serious nonlinearity and ill-posedness compared with full data ISPs (FD-ISPs). In this article, we propose a learning-based inversion approach in the frame of the U-net convolutional neural network (CNN) to quantitatively image unknown scatterers located in homogeneous background from the amplitude-only measured total field (also denoted PD). Three training schemes with different inputs to the U-net CNN are proposed and compared, i.e., the direct inversion scheme (DIS) with phaseless total field data, retrieval dominant induced currents by the Levenberg–Marquardt (LM) method (PD-DICs), and PD with contrast source inversion (PD-CSI) scheme. We also demonstrate the setup of training data and compare the performance of the three schemes using both numerical and experimental tests. It is found that the proposed PD-CSI and PD-DICs perform better in terms of accuracy, generalization ability, and robustness compared with DIS. PD-CSI has the strongest capability to tackle with PD-ISPs, which outperforms the PD-DICs and DIS.

摘要——在没有实测场数据相位信息的情况下，无相位数据逆散射问题（PD ISP）与全数据ISP（FD ISP）相比，具有更严重的非线性和病态性。在这篇文章中，我们提出了一种在U-net卷积神经网络（CNN）框架下的基于学习的反演方法，从仅测量振幅的总场（也称为PD）中定量成像位于均匀背景中的未知散射体。提出并比较了U-net CNN的三种不同输入的训练方案，即无相位全场数据的直接反演方案（DIS）、Levenberg-Marquardt（LM）方法反演主导感应电流（PD-DIC）和PD对比源反演（PD-CSI）方案。我们还演示了训练数据的设置，并使用数值和实验测试比较了三种方案的性能。研究发现，与DIS相比，所提出的PD-CSI和PD-DIC在准确性、泛化能力和鲁棒性方面表现更好。PD-CSI在处理PD-ISP方面具有最强的能力，其性能优于PD-DIC和DIS。

Uncertainty Quantification in Inverse Scattering Problems With Bayesian Convolutional Neural Networks

贝叶斯卷积神经网络在逆散射问题中的不确定性量化

1
2
3
Abstract— Recently, tremendous progress has been achieved in applying deep learning schemes (DLSs) to solve inverse scattering problems (ISPs), where state-of-the-art performance has been attained. However, little attention has been paid to the uncertainty quantification of these deep-learning methods in solving ISPs. In other words, the error of the prediction is not known since the ground truth is not available in practice. In this article, a Bayesian convolutional neural network (BCNN) is used to quantify the uncertainties in solving ISPs. With Monte Carlo dropout, the proposed BCNN is able to directly predict the pixel-based uncertainties of the widely used DLSs in ISPs. To quantitatively evaluate the performance of uncertainty predictions, both correlation coefficient and nonlinear correlation distribution between the predicted uncertainty and true absolute error are calculated. The tests on both synthetic and experimental data show that the predictive uncertainty is highly correlated with true absolute error calculated from the ground truth. Besides, when DLSs fail to solve an ISP, the predicted uncertainty increases significantly, which offers a pixel-based “confidence level” in solving ISPs.

摘要——最近，在应用深度学习方案（DLS）解决逆散射问题（ISP）方面取得了巨大进展，取得了最先进的性能。然而，很少有人关注这些深度学习方法在解决ISP问题时的不确定性量化。换句话说，由于在实践中无法获得地面真相，因此预测的误差是未知的。本文使用贝叶斯卷积神经网络（BCNN）来量化求解ISP时的不确定性。在蒙特卡洛丢弃的情况下，所提出的BCNN能够直接预测ISP中广泛使用的DLS的基于像素的不确定性。为了定量评估不确定性预测的性能，计算了预测不确定性与真实绝对误差之间的相关系数和非线性相关分布。对合成数据和实验数据的测试表明，预测不确定度与根据地面真实值计算的真实绝对误差高度相关。此外，当DLS无法解决ISP时，预测的不确定性会显著增加，这为解决ISP提供了基于像素的“置信水平”。

Physics-Inspired Convolutional Neural Network for Solving Full-Wave Inverse Scattering Problems

求解全波逆散射问题的物理启发卷积神经网络

1
2
3
Abstract— In this paper, to bridge the gap between physical knowledge and learning approaches, we propose an induced current learning method (ICLM) by incorporating merits in traditional iterative algorithms into the architecture of convolutional neural network (CNN). The main contributions of the proposed method are threefold. First, to the best of our knowledge, it is the first time that the contrast source is learned to solve full-wave inverse scattering problems (ISPs). Second, inspired by the basis-expansion strategy in the traditional iterative approach for solving ISPs, a combined loss function with multiple labels is defined in a cascaded end-to-end CNN (CEE-CNN) architecture to decrease the nonlinearity of objective function, where no additional computational cost is introduced in generating extra labels. Third, to accelerate the convergence speed and decrease the difficulties of the learning process, the proposed CEE-CNN is designed to focus on learning the minor part of the induced current by introducing several skip connections and to bypass the major part of induced current to the output layers. The proposed method is compared with the state-of-the-art of deep learning scheme and a well-known iterative ISP solver, where numerical and experimental tests are conducted to verify the proposed ICLM.

摘要——为了弥合物理知识和学习方法之间的差距，本文将传统迭代算法的优点融入卷积神经网络（CNN）的架构中，提出了一种感应电流学习方法（ICLM）。该方法的主要贡献有三方面。首先，据我们所知，这是第一次学习对比源来解决全波逆散射问题（ISP）。其次，受求解ISP的传统迭代方法中的基扩展策略的启发，在级联的端到端CNN（CEE-CNN）架构中定义了一个具有多个标签的组合损失函数，以降低目标函数的非线性，其中在生成额外标签时不引入额外的计算成本。第三，为了加快收敛速度并降低学习过程的难度，所提出的CEE-CNN被设计为通过引入几个跳跃连接来专注于学习感应电流的较小部分，并将感应电流的主要部分绕过输出层。将提出的方法与最先进的深度学习方案和著名的迭代ISP求解器进行了比较，在那里进行了数值和实验测试来验证提出的ICLM。

Precise Near-Range 3-D Image Reconstruction Based on MIMO Circular Synthetic Aperture Radar

基于MIMO圆形合成孔径雷达的精确近距离三维图像重建

1
2
3
Abstract— This article studies the near-range 3-D image reconstruction based on millimeter-wave multiple-input-multipleoutput circular synthetic aperture radar (MIMO-CSAR). We first derive the exact forward wave model of MIMO-CSAR and then propose a range migration algorithm for near-range high-precision 3-D image reconstruction. Our formulation is strictly based on wave theory. The propagation attenuation, which is an inherent factor in wave equation and is significant for near-range wide-angle sensing case, is considered and compensated efficiently with a Fourier-domain matched filtering. Besides, the phase decoupling is achieved with a 2-D Stolt mapping. The computational complexity of the algorithm is at the same level as the state-of-the-art method. Compared with the state of the art, by considering the amplitude variation, the imaging quality can be improved for near-range measurement with large beamwidth. The results from both synthetic and practical measurement data demonstrate that a wider dynamic range (less sidelobes appeared at the same dynamic level) and a better recovery for widespread targets compared with the state-of-the-art imaging method.

摘要——本文研究了基于毫米波多输入多输出圆合成孔径雷达（MIMO-CSAR）的近距离三维图像重建。我们首先推导了MIMO-CSAR的精确前向波模型，然后提出了一种用于近距离高精度三维图像重建的距离偏移算法。我们的公式严格基于波动理论。传播衰减是波动方程中的一个固有因素，对近距离广角传感情况具有重要意义，通过傅里叶域匹配滤波有效地考虑和补偿了传播衰减。此外，通过二维斯托尔特映射实现了相位解耦。该算法的计算复杂度与最先进的方法处于同一水平。与现有技术相比，通过考虑振幅变化，可以提高大波束宽度近距离测量的成像质量。合成和实际测量数据的结果表明，与最先进的成像方法相比，该方法具有更宽的动态范围（在相同的动态水平下出现的旁瓣更少）和对广泛目标的更好恢复。

Learning-Based Fast Electromagnetic Scattering Solver Through Generative Adversarial Network

基于生成对抗网络的快速电磁散射求解器

1
2
3
Abstract— This article proposes a learning-based noniterative method to solve electromagnetic (EM) scattering problems utilizing pix2pix, a popular generative adversarial network (GAN). Instead of calculating induced currents directly from a matrix inversion, a forward-induced current learning method (FICLM) is introduced to calculate the induced current through a neural-network mapping. The scattered fields can be further calculated through a multiplication of the Green’s function with the predicted induced currents. Inspired by wave physics of scattering problems, we have designed three kinds of input schemes, covering different combinations of the given incident field and permittivity contrast, to evaluate the performance of the FICLM model under both single-incidence and multi-incidence cases. Numerical results prove that the proposed FICLM outperforms the method of moments (MoM) in terms of both computational speed and accuracy by use of reference data with a higher precision. The FICLM with the direct sum of permittivity contrast and a so-called Born-type induced current, achieves the best calculation accuracy and generalization capability compared to the other two inputs. The comparison with other types of neural networks, such as U-net, also demonstrates the superior performance of FICLM for dealing with complex scatterers due to the use of adversarial framework in pix2pix. The proposed method paves a new way for the fast solution of EM-scattering problems through deep learning techniques.

摘要——本文提出了一种基于学习的非迭代方法，利用流行的生成对抗网络（GAN）pix2pix来解决电磁（EM）散射问题。引入正向感应电流学习方法（FICLM），通过神经网络映射计算感应电流，而不是直接从矩阵求逆计算感应电流。通过将格林函数与预测的感应电流相乘，可以进一步计算散射场。受散射问题的波动物理学的启发，我们设计了三种输入方案，涵盖了给定入射场和介电常数对比度的不同组合，以评估FICLM模型在单入射和多入射情况下的性能。数值结果证明，通过使用具有更高精度的参考数据，所提出的FICLM在计算速度和精度方面都优于矩量法（MoM）。与其他两个输入相比，具有电容率对比度和所谓的玻恩型感应电流的直接和的FICLM实现了最佳的计算精度和泛化能力。与其他类型的神经网络（如U-net）的比较也表明，由于在pix2pix中使用了对抗框架，FICLM在处理复杂散射体方面具有优越的性能。该方法为利用深度学习技术快速求解电磁散射问题开辟了新途径。

A类刊汇总

期刊名称 中科院大类分区 中科院小类分区 JCR分区 一般审稿周期/月 难度 是否TOP 面向领域 费用 备注
IEEE Journal On Selected Areas In Communications 一区 一区 Q1 6 难 是 无线通信网络的网络编码、医疗保健的无线和普适通信、网络基础设施配置、宽带接入网络：架构和协议、体域网络：技术和应用、水下无线通信网络、通信系统中的博弈论、在未来通信网络中利用有限反馈。 17000 通信
IEEE Transactions On Image Processing 一区 一区 Q1 8 难 是 各种应用中图像、视频和多维信号的形成、捕获、处理、通信、分析和显示的新理论、算法和架构。感兴趣的主题包括但不限于图像、视频和多维信号的数学、统计和感知建模、表示、形成、编码、过滤、增强、恢复、渲染、半调、搜索和分析。感兴趣的应用包括图像和视频通信、电子成像、生物医学成像、图像和视频系统以及遥感。 图像处理
IEEE Transactions On Industrial Electronics 一区 一区 Q1 9 难 是 电力电子和驱动控制技术、系统控制和信号处理、故障检测和诊断、电力系统、仪器仪表、测量和测试、建模和仿真、运动控制、机器人、传感器和执行器、神经网络的实现、模糊逻辑和工业系统中的人工智能、工厂自动化、通信和计算机网络 电气自动化
IEEE Transactions On Pattern Analysis And Machine Intelligence 一区 一区 Q1 7.9 难 是 计算机视觉和图像理解的所有传统领域、模式分析和识别的所有传统领域以及机器智能的选定领域的文章，特别强调用于模式分析的机器学习。还涵盖了视觉搜索技术、文档和手写分析、医学图像分析、视频和图像序列分析、基于内容的图像和视频检索、面部和手势识别以及相关的专业硬件和/或软件架构等领域。 计算机视觉、计算机，人工智能
IEEE Transactions On Systems Man & Cybernetics Systems 一区 一区 Q1 5 难 是 包括系统工程领域。它包括与大型系统的定义、开发和部署相关的任何系统工程生命周期阶段的问题制定、分析和建模、决策和问题解释。此外，它还包括系统管理、系统工程流程以及各种系统工程方法，例如优化、建模和仿真。 系统工程
Joule 一区 一区 Q1 1.5 难 是 能源 能源
Laser & Photonics Reviews 一区 一区 Q1 2 难 是 光子材料;超材料;纳米光子学;超快光子学;等离子体学;量子光子学 - 量子科学与技术;硅光子学;光-物质相互作用;合成维度;拓扑光子学;半导体光子学;LED、太阳能电池和探测器的光子学;光纤激光器和光纤;亚波长光子学;光学天线;人造材料的光子学;微/纳米腔;激光冷却和超冷气体;光流体学;光力学;激光计量和光谱学;变换光学;纳米激光器;全息摄影;生物光子学和生物医学光学;非线性光学;光吸收器;光学镀膜;光子晶体;光学成像;电信中的光学。 光学
Photonix 一区 一区 Q1 4 难 是 光纵和应用、光束传播和转向技术
光通信、存储、信息处理和计算
用于大数据和人工智能的光子学
天文光子学和航空航天光学
光学传感技术
太赫兹和 X 射线光学器件
绿色技术
小型光学元件
非线性光学
光电子学
超元光学
仿生学		 1999美元 光学
Nano Today 二区 一区 Q1 3 难 是 纳米结构材料和薄膜的合成和自组装;纳米晶体、量子点和纳米线的功能化和尺寸依赖性;纳米管和纳米多孔材料的加工和模板化;聚合物纳米颗粒、有机-无机纳米复合材料和生物杂化物的定制;纳米和微机电系统的制造;结构和功能纳米材料的设计和工程;用于生物、医疗、化学、催化、能源和环境应用的纳米系统;用于电子、光子、磁、成像、诊断和传感器应用的纳米器件 纳米科学
ACS Nano 一区 一区 Q1 2 较难 是 纳米结构（纳米材料和组装体、纳米器件和自组装结构）、纳米生物技术、纳米制造、纳米科学和纳米技术的方法和工具以及自组装和定向组装的合成、组装、表征、理论和模拟的综合文章 纳米技术
Advanced Energy Materials 一区 一区 Q1 1 较难 是 能量收集、转换和存储中使用的材料 能源
Advanced Functional Materials 一区 一区 Q1 3 较难 是 材料科学、纳米技术、液晶、半导体、超导体、光学、激光、传感器、多孔材料、发光材料、陶瓷、生物材料、磁性材料、薄膜、胶体、高级、材料、能源材料 材料
Advanced Materials 一区 一区 Q1 2.5 较难 是 材料化学和物理学 材料化学和物理学
Engineering Applications Of Artificial Intelligence 一区 一区 Q1 9 较难 是 人工智能工程应用 人工智能工程应用
IEEE Communications Surveys And Tutorials 一区 一区 Q1 1-2 较难 是 通信类综述 通信类综述
IEEE Transactions On Antennas And Propagation 一区 一区 Q1 4 较难 是 包括天线的理论和实验进展，包括设计和开发，以及电磁波传播方面的理论和实验进展，包括散射、衍射和与连续介质的相互作用;以及与天线和传播相关的应用，例如遥感、应用光学以及毫米波和亚毫米波技术
IEEE Transactions On Circuits And Systems For Video Technology 一区 一区 Q1 3 较难 是 涵盖了所有视频技术的电路和系统方面。鼓励在 TCSVT 上发表具有电路和系统视角的一般性、理论性和面向应用的论文，内容涉及图像/视频采集、表示、演示和显示或与之相关;处理、过滤和转换;分析和综合;学习和理解;压缩、传输、通信和联网;存储、检索、索引和搜索;和/或硬件和软件的设计和实施。 图像处理
IEEE Transactions On Cybernetics 一区 一区 Q1 2-3 较难 是 控制论、计算智能、计算机视觉、神经网络、遗传算法、机器学习、模糊系统、认知系统、决策和机器人技术等领域 自动化，计算机
IEEE Transactions On Geoscience And Remote Sensing 一区 一区 Q1 4 较难 是 专注于应用于传感陆地、海洋、大气和太空的科学和工程理论、概念和技术;以及这些信息的处理、解释和传播 遥感
IEEE Transactions On Industrial Informatics 一区 一区 Q1 4.5 较难 是 智能和计算机控制系统、机器人技术、工厂通信和自动化、柔性制造、视觉系统以及数据采集和信号处理 自动化
IEEE Transactions On Neural Networks And Learning Systems 一区 一区 Q1 1-2 较难 是 神经网络和相关学习系统 神经网络
IEEE Transactions On Power Electronics 一区 一区 Q1 3.2 较难 是 电力电子工程师普遍感兴趣的新型器件、电路或系统问题 电子器件、电路
IEEE Transactions On Wireless Communications 一区 一区 Q1 7 较难 是 调制和编码、检测和估计、分集技术和均衡、传播和信道表征、衰落对策、多用户检测、信号分离和干扰抑制、DSP 在无线系统中的应用、宽带无线通信、网络架构和协议，重点是物理层和链路层通信， 无线系统的自适应天线， 多址技术， 空时处理， 同步技术， 软件无线电， 资源分配和干扰管理， 多速率和多载波通信， 安全、隐私和身份验证， 实验和原型结果， 系统和服务，包括移动卫星、无线本地环路、无线局域网、无线 PBX 和 PCS/蜂窝。 通信
Light: Science&Applications 一区 一区 Q1 5 较难 是 光学和光子学相关的工程和应用科学 665欧元 光学
Microsystems & Nanoengineering 一区 一区 Q1 5 较难 是 微纳米尺度的设备和系统的新设计（理论、建模和仿真）、制造、表征、可靠性以及应用 3790美元 纳米科学
Microsystems And Nanoengineering 一区 一区 Q1 5 较难 是 微纳米尺度的设备和系统的新设计（理论、建模和仿真）、制造、表征、可靠性以及应用 3790美元 工程技术
Optica 一区 一区 Q1 4 较难 是 光学和光子学所有领域 3360美元 光学
Photonics Research 一区 一区 Q1 3 较难 是 激光器、LED 和其他光源;光纤和光通信;成像、探测器和传感器;新型材料和工程结构;光学数据存储和显示;等离子体学;量子光学;衍射光学元件和导引光学元件;医学光学和生物光子学;紫外线和 X 射线;太赫兹技术 光学
Physical Review Letters 一区 一区 Q1 2.1 较难 是 普通物理学，包括统计力学、量子力学和量子信息
引力、天体物理学和宇宙学
基本粒子和场
核物理学
原子、分子和光学物理学
非线性动力学、流体动力学和经典光学
等离子体和光束物理学
凝聚态物质和材料物理学
聚合物、软物质、生物、气候和跨学科物理学，包括网络		 物理综合
Proceedings Of The IEEE 一区 一区 Q1 1-2 较难 是 电子、电气和计算机工程以及计算机科学 电子、计算机综述
Research 一区 一区 Q1 3 较难 是 生命和物理科学的基础研究以及工程和应用科学的重要发现或问题 1200-2000美元 综合
IEEE Transactions On Microwave Theory And Techniques 一区 二区 Q2 6 较难 是 微波/毫米波元件、设备、电路和系统相关的工程和理论部分，涉及微波信号的产生、调制、解调、控制、传输和检测。这包括科学、技术和工业活动
IEEE Internet Of Things Journal 二区 一区 Q1 5 较难 是 物联网 物联网
IEEE Wireless Communications 二区 一区 Q1 1.5-3 较难 否 电话、通信掌上电脑、协议、消息传递、通信和个性化流量过滤等主题。它还涵盖了频谱分配、行业结构和技术演进等政策问题 通信
Materials Science And Engineering: A STRUCTURAL MATERIALS PROPERTIES MICROSTRUCTURE AND PROCESSING 二区 一区 Q1 2.8 较难 是 材料的基本特性、加工历史、微观结构和作环境影响的承载能力相关 材料
Computers & Industrial Engineering 二区 二区 Q1 11 较难 是 计算机和电子通信 计算机工程工业
IEEE Communications Magazine 二区 二区 Q1 1-2 较难 否 电信、多媒体、互联网和数字）、网络（包括其软件化以及底层基础设施）和设备技术、支持系统、横向主题（如应用于电信的人工智能）、市场趋势、战略和监管问题 通信
IEEE Transactions On Instrumentation And Measurement 二区 二区 Q1 6.8 较难 否 电气和电子仪器和设备开发和使用的创新解决方案的论文，以测量、监测和/或记录物理现象，以推进测量科学、方法、功能和应用。这些论文的范围可能包括：（1） 测量的理论、方法和实践;（2） 设计、开发和评估用于生成、获取、调节和处理信号的仪器和测量系统及组件;（3） 分析、表示、显示和保存从一组测量中获得的信息;（4） 为建立和维护仪器仪表和测量领域的技术标准提供科学和技术支持。 测量、仪器
IEEE Transactions On Signal Processing 二区 二区 Q1 3 较难 是 信息处理以及过滤、编码、传输、估计、检测、分析、识别、合成、记录和再现信号的理论和应用 信号处理
IEEE Transactions On Terahertz Science And Technology 二区 二区 Q1 长 较难 否 太赫兹理论、技术和应用的原始研究，涉及太赫兹波产生、传输和检测的组件、设备、电路和系统 太赫兹
International Journal Of Computer Vision 二区 二区 Q1 4.5 较难 否 计算机视觉的数学、物理和计算方面：图像形成、处理、分析和解释；机器学习技术；统计方法；传感器。应用：基于图像的渲染、计算机图形学、机器人技术、照片判读、图像检索、视频分析和注释、多媒体等。与人类感知的联系：人类视觉的计算和建筑方面。 计算机视觉
Materials & Design 二区 二区 Q1 2 较难 否 涵盖无机和有机材料的结构和特性研究、合成、加工、表征和测试的进展、材料和工程系统的设计以及技术应用。该期刊本质上是多学科的，旨在将材料科学、工程、物理和化学的各个方面结合起来 3540 美元 材料化学和物理学
ACM Transactions On Computer Systems 四区 三区 Q2 3 较难 否 计算机系统和系统软件的设计、实施、分析、评估和使用的研究和开发成果。术语“计算机系统”的解释很广，包括作系统、系统架构和硬件、分布式系统、优化编译器以及系统与计算机网络之间的交互 计算机系统（硬件）
Journal Of Machine Learning Research 四区 四区 Q1 8+ 较难 否 机器学习 机器学习
ACM Transactions On Software Engineering And Methodology 一区 一区 Q1 3 中等 是 软件系统规范、设计、开发和维护 软件系统
Chinese Journal Of Aeronautics Engineering 一区 一区 Q1 5 中等 是 航空工程和航天工程 航空航天
IEEE Transactions On Knowledge And Data Engineering 一区 一区 Q1 1-2 中等 是 计算机科学、人工智能、电气工程、计算机工程和其他适当领域的知识和数据工程方面 计算机
Mechanical Systems And Signal Processing 一区 一区 Q1 6.7 中等 是 机械、航空航天和土木工程领域的跨学科期刊，旨在报道传感、仪器仪表、信号处理、建模和动态系统控制方面的新技术产生 机械工程
Pattern Recognition 一区 一区 Q1 4.2 中等 是 模式识别、人工智能、图像处理、二维和三维匹配、专家系统和机器人技术的所有方法、技术和应用 模式识别，人工智能
Photonic Sensors 一区 一区 Q1 4 中等 是 光纤传感器、平面波导传感器、基于激光的传感器和生物光子传感器等。光子传感器侧重于与光子传感器的新原理、结构或材料相关的实验贡献 光学、传感器
Nano Letters 一区 二区 Q1 1.3 中等 是 纳米尺度物理、化学和生物现象的实验和理论结果
用物理、化学和生物方法合成、表征和加工有机、无机、聚合物和杂化纳米材料
合成、装配和交互过程的建模与仿真
高性能集成纳米结构和纳米工程器件的实现
纳米材料在生活与环境系统中的应用		 纳米材料
ACM Transactions On Information Systems 二区 一区 Q1 3 中等 否 信息检索（例如搜索引擎、推荐系统） 信息
IEEE Transactions On Services Computing 二区 一区 Q1 4 中等 是 服务计算的数学基础、面向服务的架构 （SOA）、服务的创建、开发和管理、IT 服务和业务服务之间的联系、Web 服务安全和隐私、Web 服务协议和合同、Web 服务发现和协商、Web 服务管理、Web 服务协作、Web 服务的服务质量、 Web 服务建模和性能管理， 用于构建面向服务的应用程序的解决方案框架， 复合 Web 服务创建和启用基础设施， 使用 Web 服务和 SOA 的业务和科学应用程序， 使用 Web 服务的业务流程集成和管理， 服务计算的标准和规范， 实用新型和解决方案体系结构， 实用新型和解决方案体系结构， 实用新型中的资源获取模型， 业务流程的数学基础建模、集成和管理、业务流程建模、集成和协作 web服务
Artificial Intelligence 二区 二区 Q1 9 中等 否 人工智能 人工智能
Journal Of Lightwave Technology 二区 二区 Q1 3 中等 是 光纤和电缆技术、有源和无源导波组件（光源、检测器、中继器、开关、光纤传感器等）;集成光学和光电子学;以及系统、子系统、新应用程序和独特的现场试验 光学
Measurement 二区 二区 Q1 3.8 中等 否 测量和计量基础知识、传感器、测量仪器、测量和估计技术、测量数据处理和融合算法、工厂和工业过程的评估程序和方法、系统、过程和算法的性能分析、用于测量目的的数学模型、 互联世界中的分布式测量系统。 测量
Nanophotonics 二区 二区 Q1 2 中等 否 等离子体学、超材料、基本原理和应用、纳米器件、近场光学显微镜 2650欧元 光学
Optics & Laser Technology 二区 二区 Q1 2.1 中等 是 激光与光学器件、传感器 光学
Remote Sensing 二区 二区 Q1 1 中等 否 遥感过程的各个方面，从仪器设计和信号处理到地球物理参数的检索及其在地球科学中的应用 2700 瑞士法郎 遥感
Chinese Optics Letters 二区 二区 Q2 1.8 中等 否 光学 2000元/页 光学
IEEE Transactions On Computers 二区 二区 Q2 6 中等 否 a） 计算机组织和架构;b）作系统、软件系统和通信协议;c） 实时系统和嵌入式系统;d） 数字设备、计算机组件和互连网络;e） 规范、设计、原型制作和测试方法和工具;f） 性能、容错性、可靠性、安全性和可测试性;g） 案例研究以及实验和理论评估;以及 h） 新的和重要的应用和趋势。 计算机，嵌入式
IEEE Transactions On Aerospace And Electronic Systems 二区 二区 Q1 3 较易 否 系统包括但不限于导航、航空电子、航天器、航空航天动力、雷达、声纳、遥测、国防、运输、自动化测试以及指挥和控制 工程系统
IEEE Transactions On Aerospace And Electronic Systems 二区 二区 Q1 3 较易 否 空间、空气、海洋或地面环境复杂系统的组织、设计、开发、集成和运营。这些系统包括但不限于导航、航空电子、航天器、航空航天动力、雷达、声纳、遥测、国防、运输、自动化测试以及指挥和控制 航空航天、电子系统
Plasma Sources Science And Technology 二区 二区 Q1 6 较易 否 等离子体源科学与技术 （PSST） 报告了在所有气体压力和等离子体密度范围内运行的低温等离子体和电离气体，具有不同程度的电离。PSST 的重点是这些等离子体的基础科学、它们的来源以及由它们启动或维持的物理和化学过程，这些过程通过理论、计算或实验技术得到阐明。PSST 还报告了研究低温等离子体所需的新的实验或理论衍生的基础数据（例如横截面、输运系数） 等离子体技术
Optics And Lasers In Engineering 二区 二区 Q2 3 较易 否 光学技术和工程中激光技术 光学
Physical Review Applied 二区 二区 Q2 2+ 较易 否 生物物理学、生物电子学和生物医学工程，
设备物理，
电子设备，
收集、储存和传输能源的技术，重点是可再生能源技术，
地球物理学和空间科学，
工业物理学，
磁性和自旋电子学，
超材料，
微流体，
自然或人工系统中的非线性动力学和模式形成，
纳米科学与纳米技术，
光学、光电子、光子学和光子器件，
量子信息处理，包括算法和硬件，
软物质物理学，包括颗粒和复杂流体以及活性物质。
ACM Transactions On Programming Languages & Systems 二区 二区 Q3 3 较易 否 编程语言和辅助编程任务的系统 编程
ACM Transactions On Programming Languages And Systems 二区 二区 Q3 3+ 较易 否 编程语言和辅助编程任务的系统 编程
Applied Physics Letters 二区 三区 Q2 1.4 较易 否 物理现象在科学、工程和现代技术的所有分支中的应用 115元/页
Optics Letters 二区 三区 Q2 1.5 较易 否 光学测量、光学元件和设备、大气光学、生物医学光学、傅里叶光学、集成光学、光学加工、光电子学、激光、非线性光学、光存储和全息术、光学相干、偏振、量子电子学、超快光学现象、光子晶体和光纤 660元/页 光学
Simulation Modelling Practice And Theory 三区 二区 Q1 3 较易 否 建模和仿真的理论方面，包括形式化建模、模型检查、随机数生成器、灵敏度分析、方差缩减技术、实验设计、元建模、验证和验证的方法和算法、选择和比较程序等；
建模和仿真在任何领域的方法和应用，包括计算机系统、网络、实时和嵌入式系统、移动和智能代理、制造和运输系统、管理、工程、生物医学工程、经济学、生态和环境、教育、交易处理等；
仿真语言和环境，包括特定于分布式计算、网格计算、高性能计算机或计算机网络等的语言和环境；
分布式实时仿真，仿真互操作性；
用于高性能计算仿真的工具，包括专用架构和并行计算。		 建模仿真
IEEE Sensors Journal 三区 三区 Q1 6 较易 否 传感和转导物理、化学和生物现象的设备的理论、设计、制造、制造和应用，重点是传感器和集成传感器-执行器的电子和物理方面 传感器
International Journal For Numerical Methods In Engineering 三区 三区 Q1 6 较易 否 计算工程的广泛领域做出的贡献而闻名，包括模型简化、不确定性量化、验证和确认、逆向分析和随机方法、优化、单元技术、求解技术和并行计算、损伤和断裂、微米和纳米尺度的力学、低速流体动力学、流体-结构相互作用、电磁学、耦合扩散现象、 以及误差估计和网格生成 计算物理
Sensors And Actuators A: Physical 三区 三区 Q1 3 较易 否 转导物理信号的固态器件研究和开发，光电传感器 光学、传感器
Aiaa Journal 三区 三区 Q2 1-2 较易 否 主题包括气动声学、空气动力学、燃烧、推进基础、流体力学和反应流、航空航天环境的基本方面、流体动力学、激光和相关现象、等离子体、研究仪器和设施、结构力学和材料、优化以及热力学和热化学 航天技术
IEEE Transactions On Computer-Aided Design Of Integrated Circuits And System 三区 三区 Q2 1-2 较易 否 模拟、数字、混合信号、光学或微波元件组成的集成电路和系统的计算机辅助设计 集成电路
IEEE Transactions On Electron Devices 三区 三区 Q2 4.7 较易 否 电子和离子集成电路器件和互连的理论、建模、设计、性能和可靠性相关的原创和重要贡献，涉及绝缘体、金属、有机材料、微等离子体、半导体、量子效应结构、真空器件和新兴材料，应用在生物电子学、生物医学电子学、计算、通信、显示、微机电、成像、 微致动器、纳米电子学、光电子学、光伏、功率 IC 和微型传感器 3850 电子器件
IEEE/ACM Transactions On Networking 三区 三区 Q2 1-2 较易 否 各种信息传输网络，包括有线（各种引导介质：例如，铜缆、光纤）和无线（例如，射频、 声学（例如，水下）、红外线）或这些的混合体 通信/计算机网络
IEEE Transactions On Electromagnetic Compatibility 三区 三区 Q3 2 较易 否 电磁环境;干扰控制;EMC 和 EMI 建模;高功率电磁学;EMC 标准、EMC 测量方法;计算电磁学和信号与电源完整性，应用于或直接与电磁兼容性问题相关;传输线;静电放电和闪电效果;无线和光学技术中的 EMC;印刷电路板和系统设计中的 EMC。 1200
Information And Computation 四区 四区 Q3 ？ 较易 否 理论计算机科学和信息论计算 计算机、信息论