CAD10
单频正弦信号调制的调频波的频谱分析
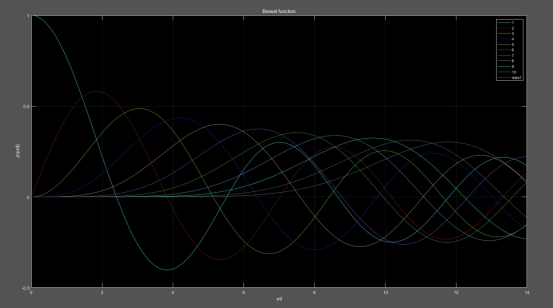
1.编写第一类Bessel函数与mF(0~10)的函数关系图。
提示:利用MATLAB中的第一类贝塞尔函数Besselj求得Jn(mF)的值。Jn(mF)=Besselj(n,mF)
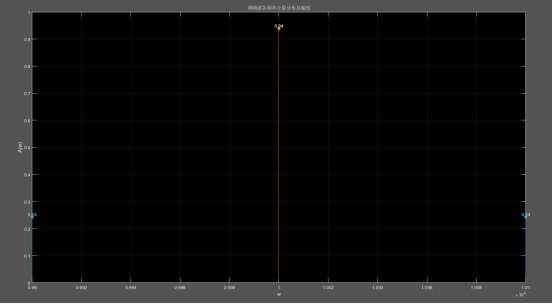
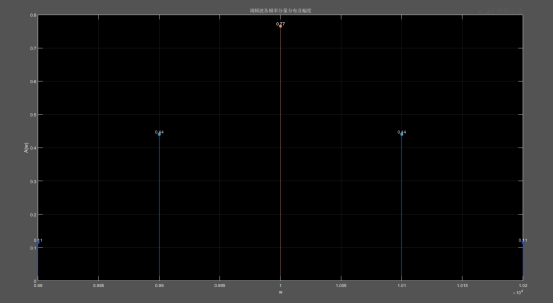
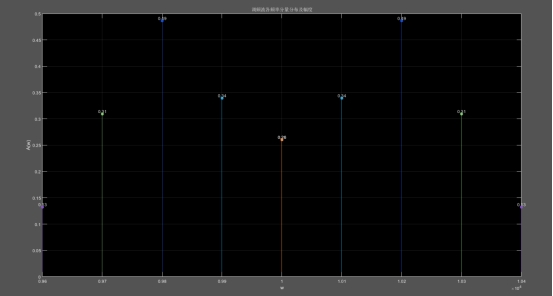
2.画出mF=0.5,1.0,3.0,5.0时,单频正弦调制的调频波的幅度频谱。
一、Matlab软件仿真
主程序:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
| n = 10;
u = 0:0.05:14;
figure (1)
for i = 0:n
J = besselj(i,u);
h = plot(u,J);
set(h,'Color',[rand,rand,rand]);
hold on;
end
xlabel('mf');
ylabel('Jn(mf)');
title('Bessel function');
grid on;
legend('1','2','3','4','5','6','7','8','9','10')
figure (2)
fm(0.5, 10000, 100)
figure (3)
fm(1, 10000, 100)
figure (4)
fm(3, 10000, 100)
figure (5)
fm(5, 10000, 100)
|
fm函数;
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
| function [] = fm (mf, wc, wf)
format long;
for i = 0:(mf+1)
J = abs(besselj(i, mf));
stem([wc-i*wf, wc+i*wf],[J, J],'fill');
s = num2str(J, 2);
h = text(wc-i*wf, J, s);
set(h, 'HorizontalAlignment', 'Center', 'VerticalAlignment', 'Bottom');
h = text(wc+i*wf, J, s);
set(h, 'HorizontalAlignment', 'Center', 'VerticalAlignment', 'Bottom');
hold on;
end
xlabel('w');
ylabel('A(w)');
title('调频波各频率分量分布及幅度');
grid on;
whitebg([0 0 0]);
hold off;
|
运行结果:
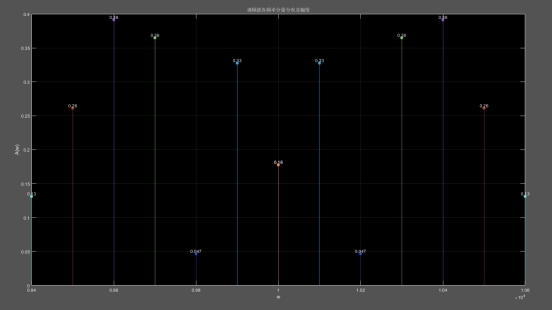
二、结果分析
调频波的幅频特性曲线幅度与Bessel函数有关,而Bessel函数又与阶数n和调频波的调制系数mF有关,理论上调频波中除了有载波频率分量之外,还包含无穷多个旁频分量,且个分量的距离是调制信号角频率Ω,各频率分量法的幅度由Bessel函数决定,但是有些幅度调制太小了,可以忽略不计。从图上可以看出,mF越大,则具有一定幅度的旁频数目越多。