《傅里叶相位恢复问题的高效数值算法及其应用研究》- 理学博士学位论文

本文以挖掘和利用模型与信号的先验信息为切入点，通过对测量过程施加预知的背景先验、自适应地从数据中学习信号特征等途径，有效降低了 FPR 问题的病态程度，进而提出了多重欠采样模型以及生成模型降低了现有算法的采样复杂度。

解集性质：

本文首先证明了当 $m < 2n − 1$ 时 FPR 问题的解集具有“花瓣状结构”；此外，通过对测量过程施加预知的背景先验以及生成网络自适应地学习数据的低维流形结构等途径，理论上证明了解的高概率唯一性，从而减少了FPR 问题的非平凡解的数量。

算法设计：

当无先验信息约束时，针对欠采样条件带来的挑战，提出了多重欠采样模型并设计 ADMM 算法进行求解；在模型先验的约束下，本文还设计 Douglas-Rachford 算法求解基于背景信息的 FPR 问题，并证明了算法在一定条件下具有局部 R 线性收敛性；基于数据先验，将 ADMM 优化算法同去噪神经网络相融合，设计了基于即插即用的 DFPR-ADMM 算法框架，通过选择不同的算子分裂方式与正则化类型得到了一系列的变种算法；最后，本文设计了 ADMM算法求解基于生成模型的 FPR 问题并分析了算法的收敛性。大量数值仿真实验以及相干衍射成像实验验证了算法在恢复效果、计算复杂度、鲁棒性等方面有着显著优势。

应用研究：

除了光学成像背景外，本文进一步研究基于同步辐射光源的穆斯堡尔谱测量问题。

相位是非常重要的物理量。周期信号的相位是实值标量，描述了在一个完整周期范围内信号每个点所处的相对位置。在波动光学中，相位的概念仅限于单色相干光场。单色相干光场中的每一个点都可以由一个复指数 $\left | a \right | e^{j\theta } $ 表示，其中 $\left | a \right | \left ( \left | a \right |^{2} \right )$ 被称为振幅 (强度)，而 $\theta$ 则称为相位。

相位恢复 (Phase Retrieval, PR) 问题，即依据 $m$ 个无相位测量 $b$ 来恢复长度为 $n$ 的信号 $x$, 是一个病态的非线性逆问题。

借鉴非凸优化以及深度学习，随机相位恢复问题的研究取得了一系列重要突破。但是，对于在工程实践中更普遍的傅里叶相位恢复 (Fourier Phase Retrieval, FPR) 问题，受限于问题的严重病态性，目前算法所需的采样数多、计算复杂度高、且鲁棒性差，远不能满足高精度实时观测的需要。

根据测量得到的光强恢复相位的问题就被称为相位恢复问题 (Phase Retrieval, PR). 若将测量算子定义为 $A$, $b$ 表示记录的光强，则 PR 问题的数学模型可以简化如下，

$$
find \enspace x ,\enspace \newline s.t. \left | A\left ( x \right ) \right | ^{2} =b
$$

其中 $x$ 是所要恢复的信号，$A$​ 为线性算子。

1、如果 $A$ 为傅里叶变换 $F$​，(1.1)则称为傅里叶相位恢复 **(Fourier Phase Retrieval, FPR)**问题

2、如果 $A$ 所对应矩阵的元素满足高斯随机分布，则称(1.1)为随机相位恢复问题

image-20240920153818856

首先，相位恢复问题(1.2)的解不唯一。可以看到，如果 $x\subseteq \mathbb{C}^{n} $ 是(1.2)的解，那么对于任意 $x\subseteq \mathbb{R} $ , $xe^{j\theta } $ 同样是(1.2)的解。除此之外，对 $x$ 进行下列操作后依然是原问题的解：1、共轭翻转： $x\left ( k \right ) \Longrightarrow \overline{x\left ( -k \right ) } $ 2、空间周期平移：$x\left ( k \right ) \Longrightarrow x\left ( k+k_{0} \right ) $

由于上述解和真实信号在结构上具有某种等价性，将它们称为平凡解。除了平凡解，相位恢复问题可能存在着非平凡解。本文所研究的相位恢复问题解的唯一性都是在关于平凡解的商空间中讨论的，换而言之，所有平凡解都视为原问题的一个解。

求解(1.2)是一个 NP 难问题。即使对于实向量 $x\subseteq \mathbb{R} $ , 通过不断变换 $b$ 中每个元素的相位来暴力搜索解集的复杂度至少为 $O(2m)$, 这在实际问题中是难以接受的。

相位恢复问题的解集往往是一个非凸集。因此，即使将(1.2)转换为一个优化问题(1.4)进行求解，问题的求解难度也不会降低。

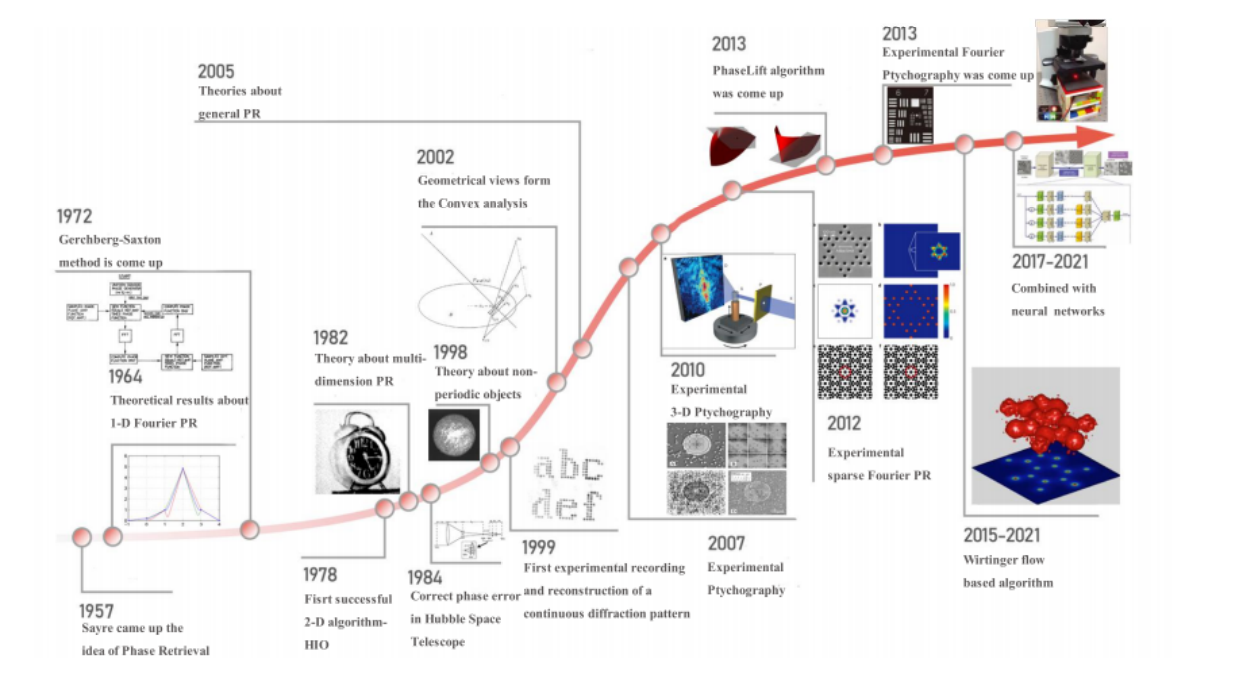
研究现状

1957 年，Sayre 首次在文献中针对 X 光晶体成像提出了相位恢复的概念。

Hofstetter 等人在 1964 第一次理论分析 FPR 问题解的性质.

1972年，Gerchberg, Saxton 等研究者提出了相位恢复领域的第一个算法—GS 算法，但该算法依旧很难恢复图像。

1978 年，来自罗切斯特大学的 Fienup 提出了 HIO 算法，并成功通过 NASA 的测试：从无相位频谱中恢复出了飞船的图像。

2017 年至今，随着深度学习的快速发展，神经网络方法也相继结合到相位恢复研究领域中并不断提升现有方法的恢复效果。

image-20240920160424683

中科院许志强研究员、香港科技大学汪扬教授主要研究高斯以及次高斯测量相位问题的解集以及在不同框架下的相位恢复问题的性质；

中科院文再文研究员以及刘歆研究员主要从实际问题出发，提出了以 ADMM、Levenberg-Marquardt 算法为代表的经典算法、；

天津师范大学常慧宾教授主要针对 Ptychography 与 Fourier Ptychography 提出了一系列经典算法；

香港科技大学蔡剑锋教授以及复旦大学魏轲研究员主要从 Riemann 优化以及损失函数的构造等角度研究随机相位恢复问题；

北京理工大学王钢教授针对随机相位恢复问题中提出了 TAF 算法、RTAF 算法等等。

解的性质分析

解的唯一性

在问题(1.2)中，直观上，测量数 $m$ 的增加有利于减少非平凡解的数量。但即使当采样数 $m ≥ 2 n−1$ 的时候，对于 1-D 信号 $x\subseteq \mathbb{C}^{n} $ , 1964 年，来自麻省理工大学的 Hofstetter 发表在 TIT 的一篇论文中证明了 FPR 问题依然可能有多达 $2^{n-2}$ 个非平凡解

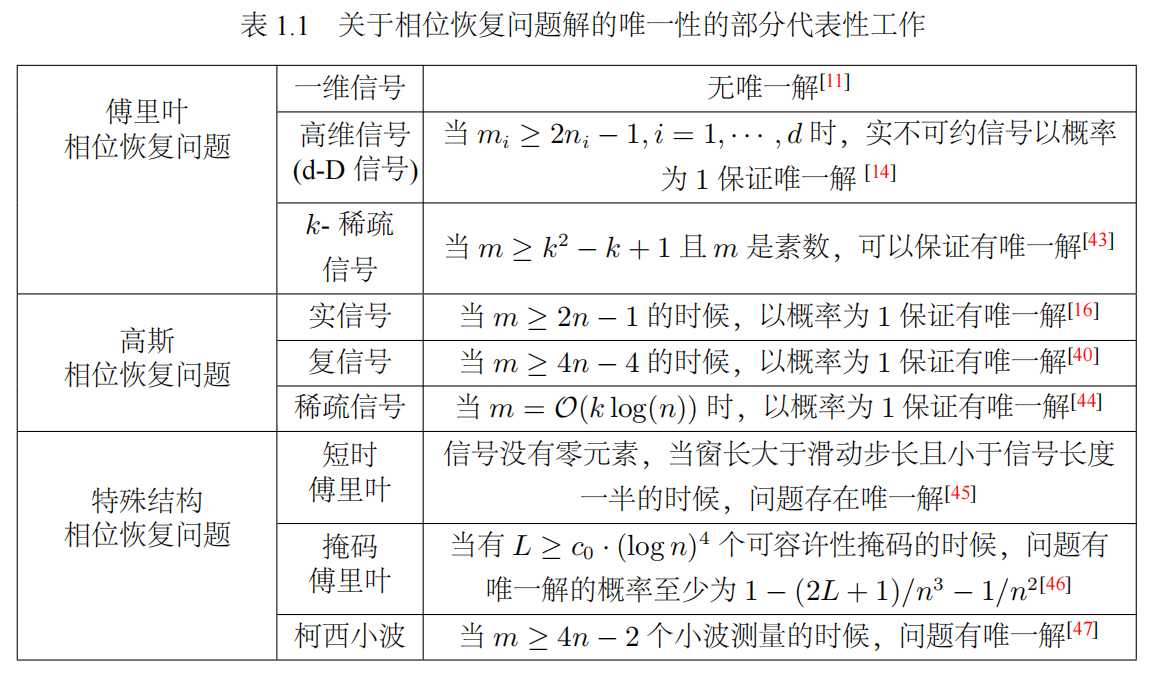
image-20240920162046172

数值算法设计

即便是 PR 问题存在唯一解，由于求解模型的非凸性，使得设计高效的求解算法也是极其挑战的。目前，关于高斯 PR 问题的算法研究成果最丰富，研究者们相继提出一系列具有收敛性保证的凸优化算法。但对于 FPR 问题，由于它的病态程度比高斯 PR 高，其主流方法依然为一系列的投影反射算法，算法往往在理论上没有收敛性保证。但它们在实际工程应用中发挥着重要的作用。本节重点介绍随机相位恢复问题以及傅里叶相位恢复问题中的经典算法。

随机相位恢复算法

image-20240922154218215

大量优化算法被相继提出求解随机相位恢复问题，这些方法可以分为两类即凸松弛算法与 Wirtinger 梯度优化算法。

凸松弛算法

基本思想：由于(1.6)的约束条件为一组二次方程，通过维数提升，这些二次方程可改写为线性方程。

image-20240922154612181

(1.7)可以转化为下列秩最小化问题

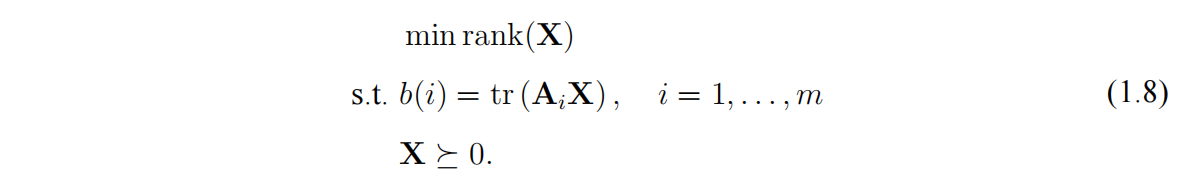
image-20240922154729950

但是(1.8)是一个比较难的组合问题。幸运的是，由于(1.8)中的约束条件是是凸的，因此可以将目标函数进行凸松弛，从而将(1.8)转换为凸优化问题。凸松弛算法的核心思想是将(1.6)转化为半定规划问题并在高维的矩阵空间中搜寻真解。因此，它在图像等数据量大的 $ x $​ 时该方法计算复杂度高。针对这个问题， Wirtinger 导数优化算法 孕育而生。

Wirtinger 导数优化算法

思想是：首先，建立关于 $x$ 与 $b$ 之间的损失函数 $ℓ(x)$, 再借助于测量向量的随机性，依据 $b$ 估计一个较好的初始值 $ x_0$ , 进而通过对$ℓ(x_0)$求 Wirtinger 导数 $∇ℓ(x_0 )$，从初始点 $x_0$ 出发沿着 Wirtinger 导数方向寻找下降步长从而不断逼近真解。其在第 $k$ 的迭代关系式如下，

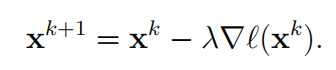
image-20240922155302942

其中 $λ$​ 为步长。在随机相位恢复问题中，常用的损失函数有下列几种形式：

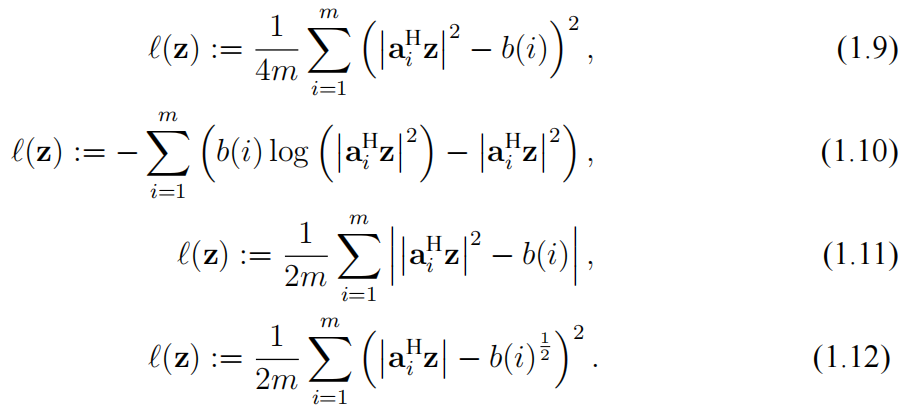
image-20240922155338057

(1.9),(1.10)和(1.11)分别对应于高斯、泊松 和拉普拉斯噪声模型下的极大似然估计函数，而(1.12)对应于振幅模型下的损失函数. (1.9)所对应的目标函数光滑，其收敛性理论较其它损失函数易于分析。但在实际中，利用 Wirtinger 算法求解(1.9), 算法的收敛速度较慢，并且需要 $m/n$ 较大的时候才能有较高的恢复率。

傅里叶相位恢复算法

image-20240922155633358

$Ω$ 是已知区域。在 X 光晶体成像以及在相干衍射成像中，$A$ 还可以设成==强度约束==或==非负约束==：

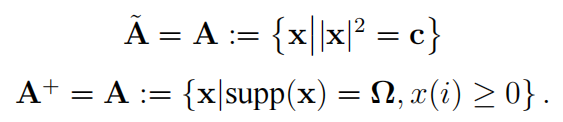
image-20240922155950891

对于傅里叶相位恢复问题，最早提出的算法被称为 GS(Gerchberg Saxton) 算法，它是一种交替投影算法。GS 方法通过将迭代值不断地交替投影到 $A$ 和 $B$ 来逼近集合交点。

image-20240922160326758

FPR 问题存在的难点及发展趋势

应该让研究者将重心从相对简单的随机相位恢复问题中转移到更贴近工程实际但比较困难的傅里叶相位恢复问题算法设计上来。而傅里叶相位恢复算法目前主要面临如下几个难点：

1、算法要求的采样复杂度高，在硬件条件受限的情况下难以适用。

2、先验信息在实际中难以挖掘与利用，传统的先验信息如稀疏以及全变差等都是人工构造的先验信息，其难以准确而全面地刻画数据的分布。

3、算法的恢复效果不理想，现有算法大多在计算复杂度与恢复质量间折衷，且问题的病态程度决定了鲁棒算法难以得到。

研究内容与结构安排

1、首先研究傅里叶相位恢复问题在欠采样条件即 $m < 2n − 1$ 情况下解集的性质，并证明了任意两个欠采样问题解集的交集与采样数 $m > 2n − 1$ 的解集相等；随后建立多重欠采样恢复模型并设计 ADMM 算法进行求解并进行收敛性分析；最后通过数值实验验证了算法具有较好的恢复效果。（二）

2、接着研究基于背景先验的相位恢复问题。通过引入充足的背景信息，本文证明了傅里叶相位恢复问题能够保证相位恢复问题的解具有真正意义下的唯一性，即去除了一切平凡解以及非平凡解。（三）

3、设计了 DR 算法求解基于背景信息的相位恢复模型。基于此模型，理论证明了 DR 算法在初始值较好的条件下能够具有 R 线性收敛性。数值实验验证了 DR 算法能够较好地收敛到真解，相干衍射成像实验也同样验证了背景信息模型的有效性。（三）

4、通过综合利用数据和模型先验，研究了基于神经网络的 FPR 算法设计。首先，将由网络所学习得到的正则化约束融合到优化模型中，进而设计基于神经网络的DFPR ADMM 算法求解傅里叶相位恢复问题。该算法在保持 ADMM 优化算法灵活的迭代格式的情况下，又继承了神经网络强大的特征表示能力，并在理论上分析了该算法的收敛性。（四）

5、研究基于生成模型的傅里叶相位恢复问题。在生成模型的约束下，证明了相位恢复问题的解具有真正的唯一性；随后设计求解生成模型的 ADMM 算法，并在理论上证明了算法的收敛性，数值算法同样验证了算法具有较好的恢复效果。（五）

6、研究了基于穆斯堡尔谱测量的相位恢复问题，设计了一套低复杂、高效的算法流程来解决穆斯堡尔谱测量问题。（六）

欠采样傅里叶相位恢复问题（二）

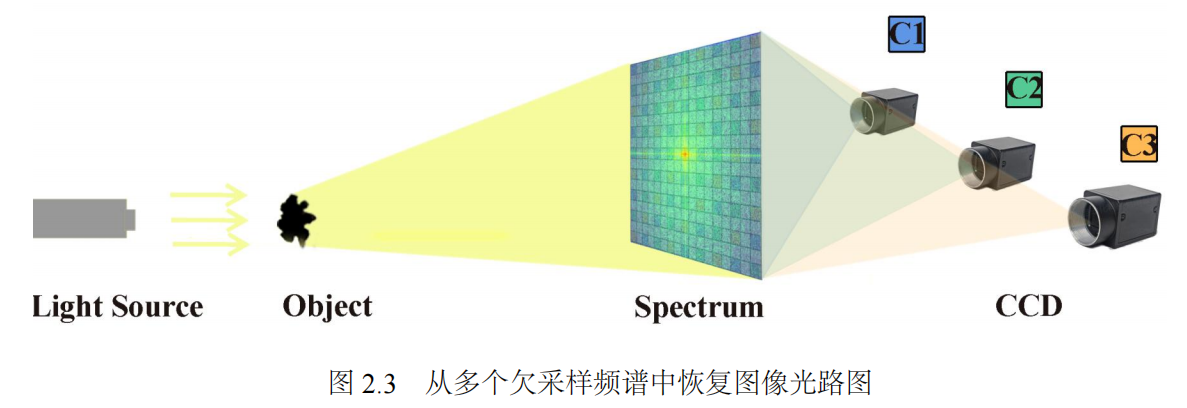
image-20240922164407308

图2.3展示了从多个欠采样频谱中恢复图像的光路示意图。由相干光源射出的光线经物体 $X$ 产生衍射图样，在远场利用三台低采样率的相机 $C_i , i = 1, · · · , 3,$ 从不同频点上采样得到无相位频谱 $B_i , i = 1, · · · , 3$. 最后，从$B_i , i = 1, · · · , 3 $ 反演得到真实图像 $X$. 余下的章节将重点阐述这一重建过程。

基于模型先验的傅里叶相位恢复（三）

研究高效可行的先验信息用以约束 FPR 问题的解集，从而降低算法的复杂度，提升恢复信号的质量。

在 FPR 问题中，研究者们已经提出了一系列的先验信息用于改善相位恢复问题的病态程度。比如，通过引入预知待求信号的部分相位、强度或者加入参考光以及二值编码，从而保证了 FPR 问题在全局相位意义下具有唯一解。对于 FPR 问题在一系列特定先验信息情况下具有唯一解做了系统的综述。此外，稀疏先验也被用于 FPR 问题, 并得到了一系列高效算法。

尽管目前已有大量利用先验信息约束 FPR 问题的工作，但是依然存在以下问题。第一，先验信息在实际应用中很难实现。第二，模型引入先验信息后，算法的复杂度较高。第三，现有算法对初始值和参数也非常敏感，容易收敛到局部最优点。

针对以上现状，本章提出一种基于背景先验的新型 FPR 模型，与已有的工作不同，该模型在光学上更加容易实现，而且由此设计的数值算法复杂度较低，具有实时成像的能力。

1
2
3
1、对于基于背景先验的 FPR 问题，在理论上，我们进一步地降低了唯一性对背景先验数量的要求。
	本章证明了对于 2-D 图像，如果背景先验在两个方向上的长度为原图像的 1.6 倍，
	就可以以概率为 1 地保证 FPR 问题的解具有唯一性。
1
2
3
2、对于求解 FPR 问题的投影梯度方法给出了收敛性证明。
	另外，本章还提出了 DR 算法用于求解基于背景先验的 FPR 问题。
	在特定的假设条件下，证明了只要初始值能够足够接近真实解，能够具有 R 线性收敛速度。
1
3、通过大量数值实验以及光学成像实验验证了 DR 算法求解基于背景先验的相位恢复模型的高效性。
### 利用背景先验的 **FPR** 模型
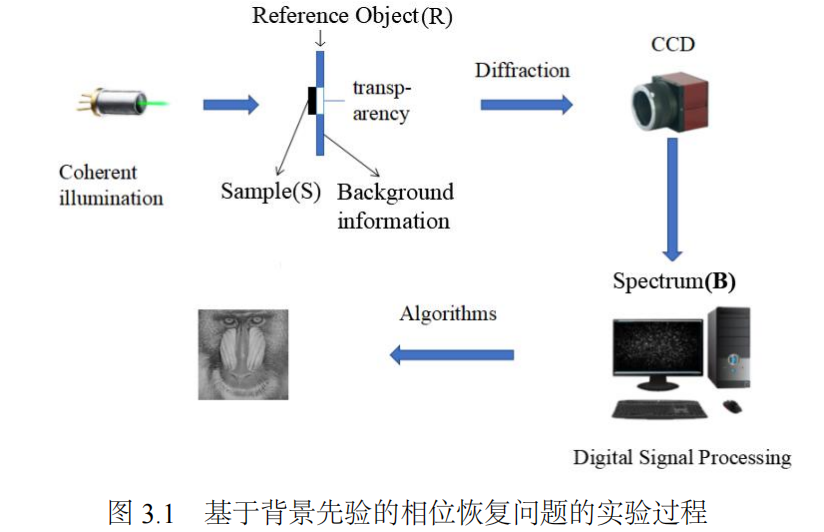
image-20240922170106209

我们提出了基于背景先验的 FPR 模型，其物理实现过程如图3.1所示。待测样本 S 被放到了参考板 R 上，R 与 S 交叠的部分是透明的。在实际应用中，R 可以使用空间光调制器 (Spatial Light Modulator, SLM), 它可以用来调节透过光的区域，从而保证样品和参考板交叠的部分能够无损失的透过光。而在焦平面上的CCD 相机仅仅记录衍射图像的强度信息 $b\in \mathbb{R}^{m_1\times m_2} $ 。 S, R 以及它们的组合被相应地定义为 $X\in \mathbb{R}^{n_1\times n_2} $ ，$Y\in \mathbb{R}^{(m_1+n_1)\times (m_2+n_2)} $，$Z\in \mathbb{R}^{(m_1+n_1)\times (m_2+n_2)} $。正如上文所述，$Y_{i,h}=0,(i,h)\in \Omega $，其中 $Ω$ 是交叠的区域。

从而基于背景先验的相位恢复问题的数学模型可以表示如下：

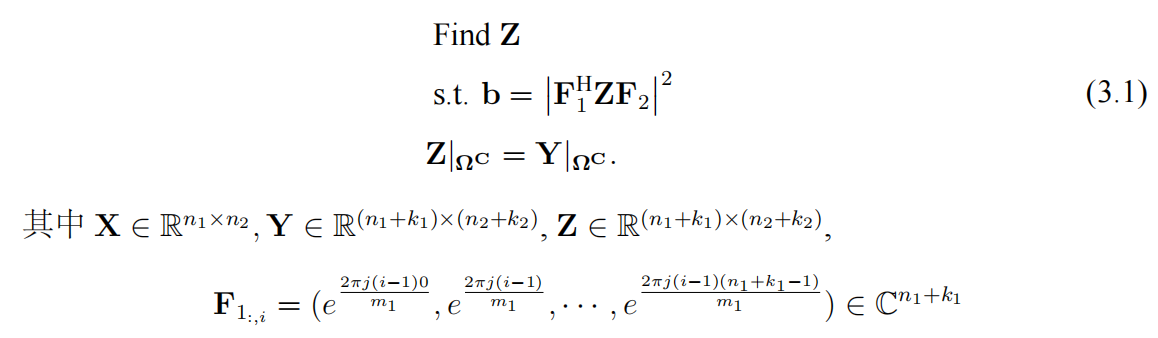
image-20240922171956854 image-20240922172145505

在文献 [83] 中，我们证明了对于 2-D 图像，如果满足下列条件之一，(3.1) 有唯一解。

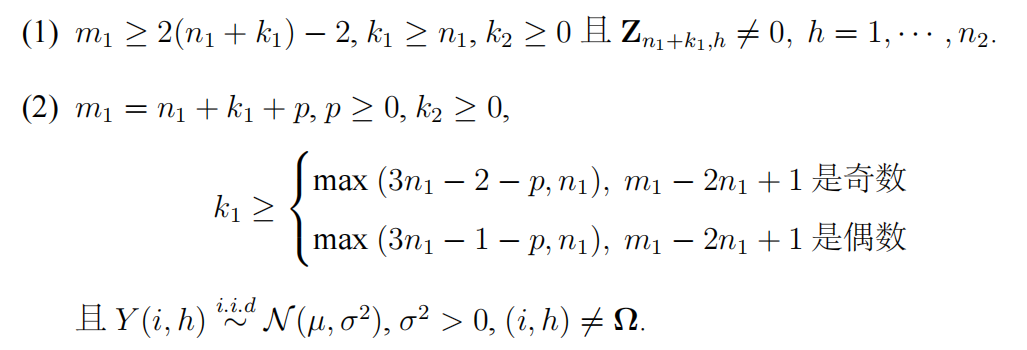
image-20240922172230844

从上述的结论可以看到，已知背景信号长度 $k_1$ 大概需要是信号 $n_1$ 的 ==3== 倍，这个要求使得实际成像过程可能很难满足。特别是当 $n_1$ 非常大的时候，物体并上背景先验可能会超过了光圈范围以及 CCD 分辨率。因此，理论中的条件在实际应用中可能无法达到。

注意到，上述理论没有对 $k_2$ 有其它额外的要求。因此，考虑通过利用 2-D图像的自相关函数来约束 $k_2$, 从而降低唯一性条件对背景先验数量的要求。由于在 [77] 已证，过采样即 $m_1 ≥ n_1 + k_1$, $m_2 ≥ n_2 + k_2$ 能够降低保证 FPR 问题唯一性所需的背景先验数量。因此，本节下面的分析仅考虑当$m_1 = n_1 + k_1$, $m_2 = n_2 + k_2$​ 的情况。

算法设计与分析

投影梯度 PGD 算法

假设我们能够有足以保证模型 (3.7) 具有唯一解的背景先验，本节考虑在此前提下设计算法求解 (3.7). 我们首先分析现有的投影梯度 PGD 算法的收敛性，随后设计 DR 方法来提高 PGD 的性能，并分析 DR 算法的收敛性。

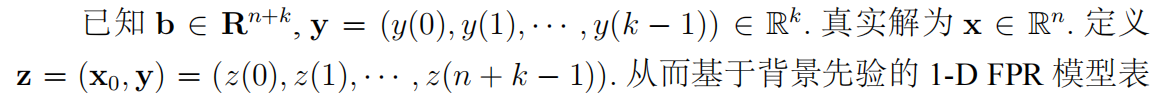
image-20240922173644471 image-20240922173701918

定义集合 $A$ 和 $B$,

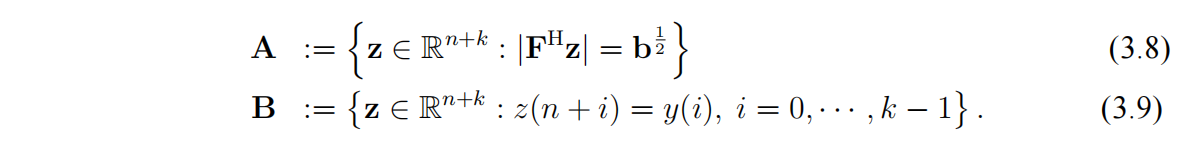
image-20240922174130952

矩阵 $A$ 和 $B$ 是闭集，但 $A$ 不是凸集。显然 $A ∩ B$ 是(3.7)的解集。定义 $z ∈ R^ {n+k}$ 在集合 $C$ 上的投影为

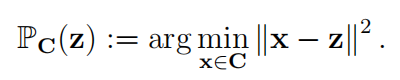
image-20240922174311475

(3.7) 可转换为下列带约束的优化问题

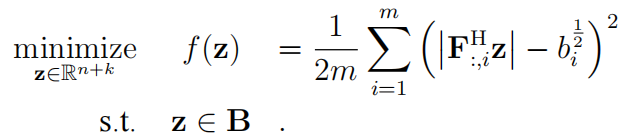
image-20240922174550832

用投影梯度方法 (Projection Gradient Descent,PGD) 求解(3.7)是一种简单而直观的方法，第 $p$ 步为

image-20240922174714918

该方法容易收敛到局部最优解并且在实际过程中需要 $k≥6n$ 。

DR算法

在大量文献中，利用平面反射的 DR(Douglas Rachford) 算法，在一定程度上具有跳出局部最优解的能力，其更适合求解(3.7). 为此，我们设计了求解3.7的 DR 算法，

输入: ${b, y, ε, T}$

​ $b$: 无相位傅里叶测量。

​ $y$: 背景先验。

​ $ε$: 给定的误差界。

​ $T$: 允许的最大迭代步骤。

输出:

​ $x$: 对于真实信号 $x$ 的估计值。

image-20240922175529573

PGD 方法和 DR 方法最大不同在于它更新迭代值的方式。对于 PGD 方法，在第 $p$ 步的时候，它通过交替投影将 $z^p$ 向集合 $A ∩ B$ 投影，所以 PGD 方法可能不收敛。另外，即使 PGD 方法收敛，它所对应的不动点 $\overline{z} $ 在实际中距离真解也可能较远。但是，如定理3.3所示，DR 方法能够保证 $\mathbb{P} _B(\overline{z} )$ 就是(3.7)的真解。

对于 DR 方法，若定义算子

image-20240922183335422

算法3.1的一个主要优势是如果找到了算法的不动点，就找到了问题的真解。

实验测试

image-20240922185203208

如图3.9(a)所示，测量得到的衍射图样的大小为 480 × 480. 基于这个无相位频谱数据，由 HIO 重建的清晰图像如图3.9(b)所示。但是，图像是从带宽较大的频谱中恢复的。实际中，由于相机限制，可能很难得到物体较大带宽的频谱。因此，如何从频率信息较少的无相位测量中恢复图像非常有必要。在剩下的测试中，我们假设获得的频谱区域为 200 × 200，如图3.10(a)所示。接下来，如3.10(b)中所示，使用图3.10(a)中的 HIO 算法无法从 200 × 200 频谱中重建可识别的图像，这是因为丢失了许多高频信息。

image-20240922185328878

利用图3.10(a)中的相同光谱，我们使用背景先验模型来恢复图像。背景先验的长度 (即图3.9(b)中的 200 × 200 图像的一部分) 为 $0.5n$. 然后使用第 DR 方法恢复图像，结果如图3.10(c)所示。我们可以发现，借助背景先验，可以从 200 × 200频谱中恢复“5”的轮廓。通过 DR 算法恢复的图像质量不是很高，这可能归因于缺乏足够的背景先验。但是，它充分证明了背景先验模型的优势。

基于即插即用神经网络的傅里叶相位恢复（四）

在求解包含 PR 在内的逆问题中，一种重要的思想是添加正则项对问题进行约束，从而降低逆问题的病态程度。正则项一方面要准确描述信号所遵循的规律；另一方面，正则项加入后的优化问题还要便于求解。因此，尽管利用上述正则项能够在求解 FPR 问题时获得一定的性能提升，但是鉴于真实信号的复杂性，准确而全面地刻画其特征是非常困难的，现有的正则项大都只能代表其部分重要特征。

近年来，很多算法致力于将神经网络同优化模型相结合来提升算法的灵活性与鲁棒性，而即插即用方法 (Plug and Play, PnP) 和噪声约束方法(Regularization by Denoising, RED) 正是两类基于数据先验的代表方法 . 它们在超分辨、压缩感知等应用中表现出色。DFPR-PnP 类算法对初始值不太敏感，能够在低信噪比情况下恢复得到更好效果

的图像

1、首先，提出名为去噪傅里叶相位恢复 DFPR(Denoising Fourier Phase Retrieval)的优化模型求解 FPR 问题。

2、设计了 DFPR-PnP ADMM 算法求解该模型。理论上证明了 DFPR-PnP ADMM 方法在一定条件下能够收敛到稳定点。

3、DFPR-PnP ADMM 能够推导出一系列的方法，从而可以将经典的傅里叶相位恢复算法同去噪神经网络相结合形成一系列变种算法。

即插即用算法设计

PnP 与 RED

根据贝叶斯极大似然估计, PnP 方法隐式地假设存在去噪器 $D_{\sigma } (\cdot )$ ，其输出结果逼近下列优化问题的最优解：

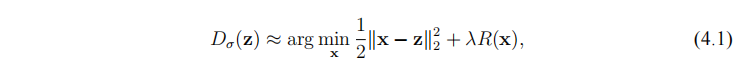
image-20240922204746248

其中 $σ$ 是噪声参数，较大的 $σ$ 意味着去噪器的强度越大。$λ > 0$ 是控制 $R(x)$ 正则化效果的参数。值得注意的是，相比于传统正则化方法，(4.1)中的正则项 $R(·)$ 是没有解析表达式的。$z$ 可以看做是 $x$​ 添加了高斯噪声的测量。

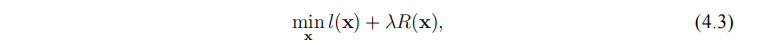
image-20240922205224811

RED 方法需要在损失函数(4.3)中显式地构造正则项。其中 $l(x)$ 是损失函数, $R(x) = \frac{1}{2} x^{T}(x-D_{\sigma }(x) ) $ , $D_σ(·)$ 为去噪器。尽管 RED 方法的正则项 $R(x)$ 拥有显式结构，但是这种结构是为了约束 $x$ 与$ x − D_σ(x)$ 的相关程度，这间接强迫了 $D_σ(x)$ 需要尽可能地去除与 $x$ 无关的信息。

即插即用 FPR 模型

为了简化分析, 我们仅讨论 1-D 情况下的 FPR 问题。实际上，1-D 的结果可以推广到 2-D 的情形。本章基于 $x$ 的结构特征引入正则约束，因此将要考虑实值信号 $x$. 假设待恢复的信号 $x\in \mathbb{R}^{n} $ , 无相位 Fourier 频谱为 $b\in \mathbb{R}^{m} $, $m\ge n$. 为了能够利用正交 Fourier 变换，我们将信号 $x$ 补零转换为长度为 $m$ 的信号。与第三章类似，定义：

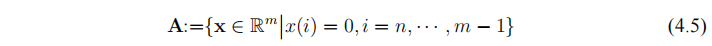
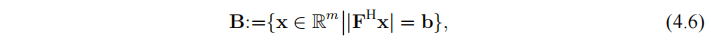
image-20240922210908102 image-20240922210919280

其中 $F\in \mathbb{C} ^{m\times m} $ 为正交傅里叶矩阵。如果 $x_0 ∈ A∩B$, 则 $P_T (x_0):=(x_0(0), · · · , x_0(n−1)) $是 FPR 问题的解, 其中 $P_T (·)$ 是截断算子, 它截去信号 $x_0\in \mathbb{R} ^{m} $ 最后 $m − n$ 个元素。由于 $B$ 为非凸集，寻找集合 $A$ 和 $B$​​ 的交点是一个棘手的问题。为了提高算法的收敛效果，在非凸问题中常常加入正则项以减轻问题的病态程度。正则项中包含了真实信号的先验信息。

去噪傅里叶相位恢复模型 (Denoising Fourier Phase Retrieval,DFPR):

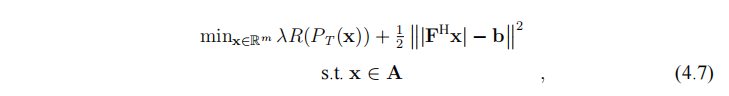
image-20240922211754489

令 $P_T (x) = z$,

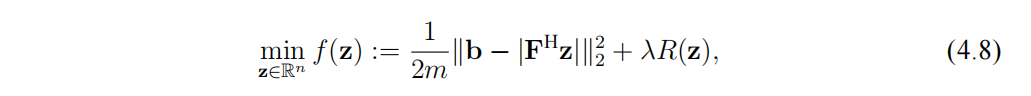
image-20240922212032330

其中 $F\in \mathbb{C} ^{m\times m} $ 为标准傅里叶矩阵。(4.8)是文献中所使用的优化模型。与(4.8)相比，(4.7)将变量提升到 $m$ 维空间中，并在 $n$​ 维空间对信号进行正则约束。和第一章类似，通过在两个维度空间交替更新信号，有望提升算法恢复效果。下面将设计 ADMM 算法求解 (4.7).

DFPR-PnP ADMM算法

加入松弛变量 $y$ 和对偶变量 $ω$

image-20240922212220734

DFPR-PnP ADMM方法的变量拥有更高的维数即 $m > n$. 因此，在高维空间和低维空间中交替极小化损失函数，则更有可能跳出低维空间中的局部最优点。DFPR-PnP ADMM 方法是一种 DR 方法, 它可以克服不动点所带来的影响，在实际应用中，DR 算法的变种即 HIO 算法能够有效地避免更快的收敛到局部最优点，并且该方法已经是傅里叶相位恢复领域中的经典算法。

DFPR-PnP HIO 算法
image-20240922212841954

即插即用算法的推广

算法4.1是一种算法框架。通过使用前文所介绍的算子分裂方法和不同的正则项 R(·) 可以推导出一系列不同的方法。

算子分裂变形、正则化子变形、基于 RED 正则约束的多重欠采样模型

实验测试

对于 DFPR-PnP ADMM, $η = 0.95$, $γ = 1.1$, $ρ_0 = 5 × 10^{−4}$, $β = 0.95$. 对于 DFPR-HIO 以及 DFPR-RED, 我们在迭代步骤中逐渐改变 $σ_k$ 的取值。DFPRRED 总共运行 800 次迭代。$D_σ$ 的初始标准差为 60. 随后每隔 200 步, 顺次下降为40, 20, 10. 对于 DFPR-RED 的每一步, 将会有 5 步内循环 ($M=5$) 来估计 (4.27) 的根。输出的结果是具有最小误差的 $∥|F^Hx| − b∥$ 历史最优解。为了公平性, 其它算法的总共迭代步数为 4000. 在 DFPR-RED 算法中, $β = 0.95$, 并且 $λ = 1$. 对于DFPR-PnP HIO 算法，$β = 0.9$.

image-20240923095510425

Tokyo, Baboon, 以及 Pillars of Creation 恢复情况可视化结果。图像大小为 256 × 256，它们是从 4 倍过采样的无相位傅里叶测量中所恢复的 (信噪比 SNR= 34 dB). 分别记录 HIO,OSS, ADMM, prDeep, DFPR-PnP ADMM, DFPR-PnP HIO 以及 DFPR-RED 算法所恢复图像的峰值信噪比 PSNR.

与几乎所有傅立叶相位恢复问题算法的实验一样，用于测试该算法的频谱经过 4 倍过采样 (m/n = 2). 在测试中，所测得的频谱被 3 种不同噪声水平的高斯白噪声所污染 (SNR=34 dB, 41 dB, 49 dB). 我们将 18 张测试图像分为两个部分：自然图像和非自然图像。在每个噪声水平下，每种算法通过不同的初始化运行 20 。最后对于每种算法，我们记录平均运行时间 $t$，平均最高峰值信噪比 (PSNR)1即PSNR 以及相应的 PSNR 的标准偏差作为评估指标。

在表4.1中，我们发现基于 DFPR 的算法表现最好，它拥有最高的 PSNR，较其它方法高出了近 10dB. 这表明基于 DFPR 的算法对噪声非常鲁棒，并且能够较好地恢复图像。尽管使用 DnCNN 的算法比 HIO，OSS 和 ADMM 花费更多的时间。但是，与 prDeep 相比，基于 DFPR 的算法以较低的计算成本获得了更好的结果。所有算法的 PSNR 的标准差都很大。对于像 Fourier PR 这样的非凸问题，这种现象是正常的。但是基于 DFPR 的算法具有较小的标准差值，这证明了算法的稳定性。尽管 DnCNN 的训练集仅包含自然图像，但基于 DFPR 的算法仍能很好地恢复非自然图像，这表明这些算法具有更广泛的应用范围。此外，我们还发现DFPR-PnP HIO 倾向于恢复非自然图像，而 DFPR-RED 更适合于重建自然图像。