一、 实验名称

PCM编码调制的MATLAB实现

二、 实验原理

请详述 PCM 抽样、量化、编码原理

PCM 抽样：脉冲编码调制就是把一个时间连续，取值连续的模拟信号变换成时间离散，取值离散的数字信号后在信道中传输。脉冲编码调制就是对模拟信号先抽样，再对样值幅度量化，编码的过程。

量化：抽样信号虽然是时间轴上离散的信号，但仍然是模拟信号，其样值在一定的取值范围内，可有无限多个值。显然，对无限个样值一一给出数字码组来对应是不可能的。为了实现以数字码表示样值，必须采用“四舍五入”的方法把样值分级“取整”，使一定取值范围内的样值由无限多个值变为有限个值。这一过程称为量化。

编码：量化后的抽样信号在一定的取值范围内仅有有限个可取的样值，且信号正、负幅度分布的对称性使正、负样值的个数相等，正、负向的量化级对称分布。若将有限个 量化样值的绝对值从小到大依次排列，并对应地依次赋予一个十进制数字代码（例如，赋予样值0的十进制数字代码为0），在码前以“+”、“-”号为前缀，来区分样值的正、负，则量化后的抽样信号就转化为按抽样时序排列的一串十进制数字码流，即十进制数字信号。简单高效的数据系统是二进制码系统，因此，应将十 进制数字代码变换成二进制编码。根据十进制数字代码的总个数，可以确定所需二进制编码的位数，即字长。这种把量化的抽样信号变换成给定字长的二进制码流的过程称为编码。

三、 仿真源程序及注释

1、均匀量化输出结果

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
clc
clear all
fs = 100000;
t = 0:1/fs:10;
ts = 0:0.3:10;

xt = 0.1.*cos(0.15.*t)+1.5.*sin(2.5.*t)+0.5.*cos(4.*t);%原始输入信号
xn = 0.1.*cos(0.15.*ts)+1.5.*sin(2.5.*ts)+0.5.*cos(4.*ts);%抽样后信号
bm = [];

% 采用均匀量化， -3v ~ 3v 量化层数为4
% 3~1.5v -> 11 ;1.5~0v -> 10 ;-1.5~0v -> 00 ;-3~-1.5v -> 01 

for i = 1:length(xn)    
    if (xn(i)>=-3)&&(xn(i)<-1.5)
        xjn(i) = -2.25;
        bm = [bm,0,1];
    end
    if (xn(i)>=-1.5)&&(xn(i)<0)
            xjn(i) = -0.75;
            bm = [bm,0,0];
        end
    if (xn(i)>=0)&&(xn(i)<1.5)
            xjn(i) = 0.75;
            bm = [bm,1,0];
        end
    if (xn(i)>=1.5)&&(xn(i)<3)
            xjn(i) = 2.25;
            bm = [bm,1,1];
        end
end

figure(1)
subplot(4,1,1)
plot(t,xt)
title('原始输入信号')
ylabel('x(t)');
xlabel('t');
axis([0 10 -3 3]);
hold on
subplot(4,1,2)
stem(1:length(xn),xn)
title('抽样后信号')
ylabel('x(n)');
xlabel('n');
axis([0 length(xn) -3 3]);
hold on
subplot(4,1,3)
stem(1:length(xn),xjn)
title('量化输出信号')
ylabel('x^(n)');
xlabel('n');
axis([0 length(xn) -3 3]);
hold on
subplot(4,1,4)
stem(1:length(bm),bm)
title('编码结果')
axis([0 length(bm) -0.1 1.1]);
hold on

2、非均匀量化输出结果

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
clc
clear all
fs = 100000;
t = 0:1/fs:10;
ts = 0:0.3:10;

xt = 0.1.*cos(0.15.*t)+1.5.*sin(2.5.*t)+0.5.*cos(4.*t);%原始输入信号
xny = 0.1.*cos(0.15.*ts)+1.5.*sin(2.5.*ts)+0.5.*cos(4.*ts);%抽样后信号
bm = [];

for i=1:length(xny)
    if xny(i)>0 %确定极性码
        B1=1;
    else
        B1=0;
    end
    xn(i)=abs(xny(i));
    C=[0 16 32 64 128 256 512 1024 2048];%A律13折现非均匀区间
    for j=1:length(C);
        if xn(i)>=C(j)&&xn(i)<=C(j+1)
            L=j-1;
            L1=dec2bin(L,3);
            B2=L1(1);
            B2=str2num(B2);
            B3=L1(2);
            B3=str2num(B3);
            B4=L1(3);
            B4=str2num(B4);
        end
    end
    a=C(L+1);%确定段内码
    b=C(L+2);
    [B5,a1,b1]=judge(xn(i),a,b);
    [B6,a2,b2]=judge(xn(i),a1,b1);
    [B7,a3,b3]=judge(xn(i),a2,b2);
    [B8,a4,b4]=judge(xn(i),a3,b3);
    result(i,1)=B1;
    result(i,2)=B2;
    result(i,3)=B3;
    result(i,4)=B4;
    result(i,5)=B5;
    result(i,6)=B6;
    result(i,7)=B7;
    result(i,8)=B8;
    bm = [bm,B1,B2,B3,B4,B5,B6,B7,B8];
end
%以下为A律13折线译码
C2=[0,16;16,32;32,64;64,128;128,256;256,512;512,1024;1024,2048];
step=[1,1,2,4,8,16,32,64];
for i=1:length(xny)
    temp(i,1)=result(i,1);
    temp(i,2)=bin2dec(num2str(result(i,2:4)));
    temp(i,3)=bin2dec(num2str(result(i,5:8)));
end
for i=1:length(xny)
    position=floor((xn(i)-C2(temp(i,2)+1,1))/step(temp(i,2)+1));
    result2(i)=C2(temp(i,2)+1,1)+position*step(temp(i,2)+1)+0.5*step(temp(i,2)+1);
    if temp(i,1)==0
        result2(i)=-result2(i);
    end
end

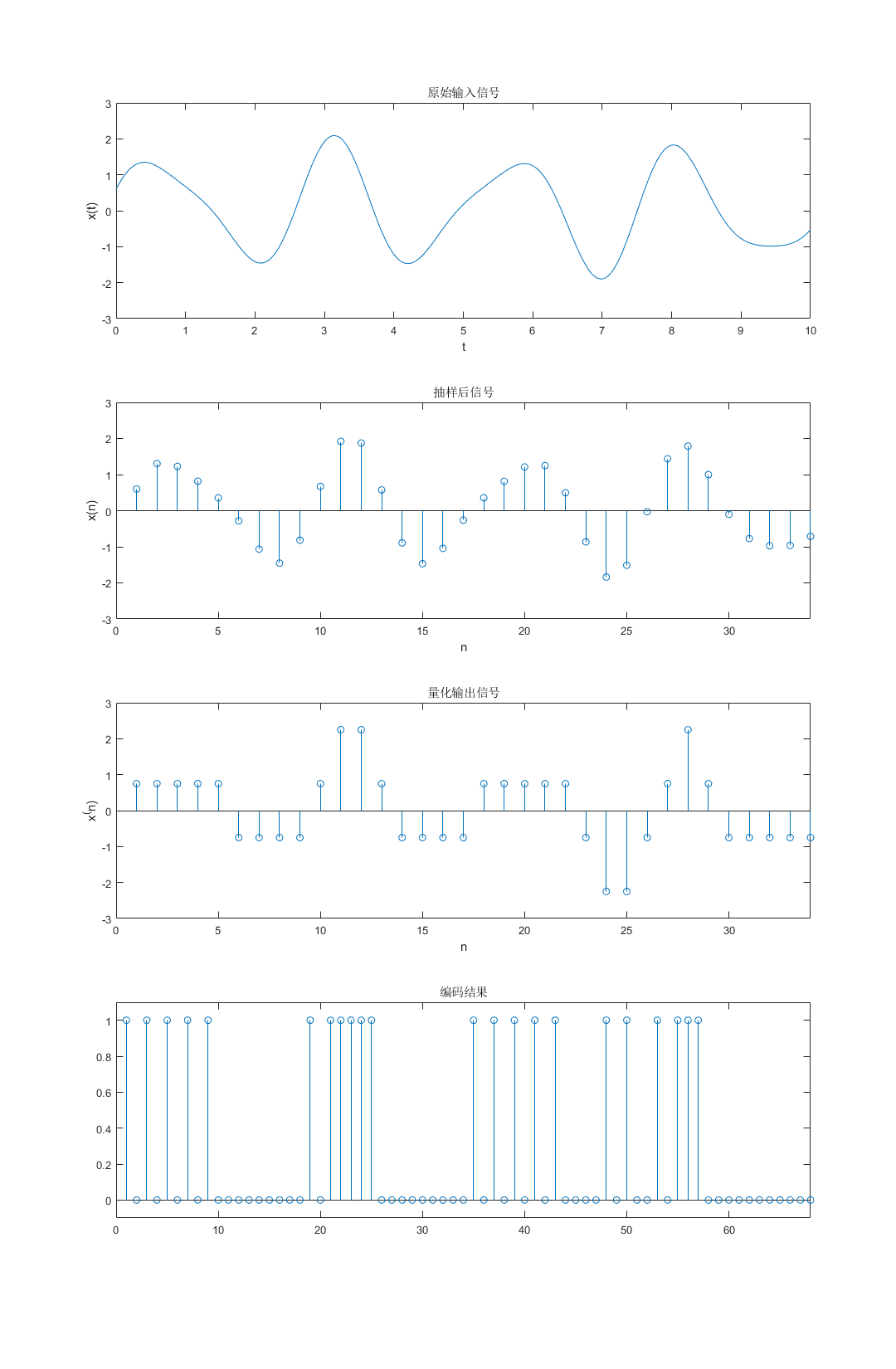
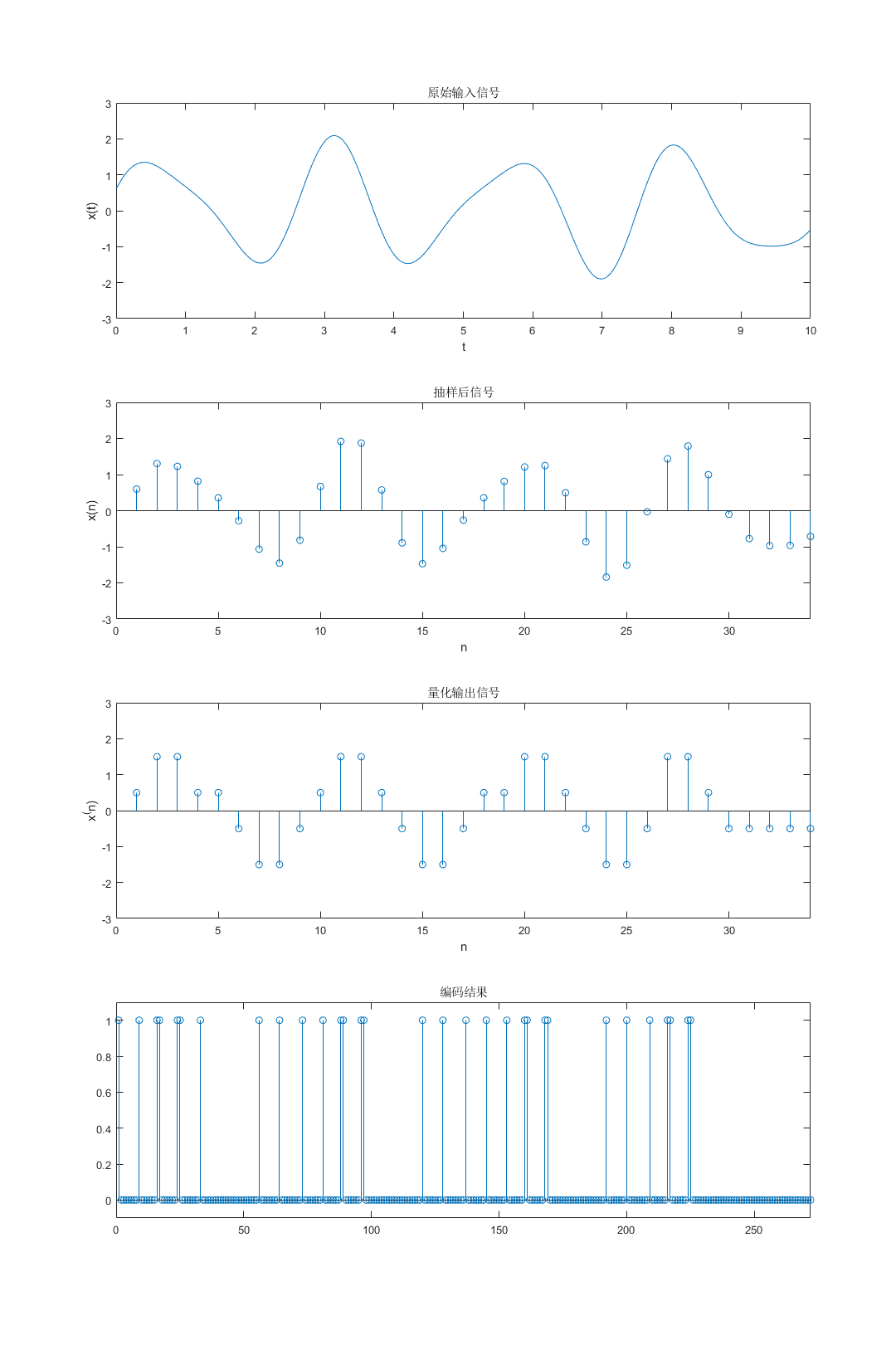
figure(1)
subplot(4,1,1)
plot(t,xt)
title('原始输入信号')
ylabel('x(t)');
xlabel('t');
axis([0 10 -3 3]);
hold on
subplot(4,1,2)
stem(1:length(xny),xny)
title('抽样后信号')
ylabel('x(n)');
xlabel('n');
axis([0 length(xny) -3 3]);
hold on
subplot(4,1,3)
stem(1:length(result2),result2)
title('量化输出信号')
ylabel('x^(n)');
xlabel('n');
axis([0 length(result2) -3 3]);
hold on
subplot(4,1,4)
stem(1:length(bm),bm)
title('编码结果')
axis([0 length(bm) -0.1 1.1]);
hold on
1
2
3
4
5
6
7
8
9
10
11
%judge函数
function [B,m1,n1]=judge(I,m,n)
if I>=m&&I<(m+n)/2
    B=0;
    m1=m;
    n1=(m+n)/2;
else
    B=1;
    m1=(m+n)/2;
    n1=n;
end

四、 仿真结果图

1、均匀量化输出结果

1）原始输入信号； 2）抽样后信号； 3）量化输出信号； 4）编码结果。

1

2、非均匀量化输出结果

1）原始输入信号； 2）抽样后信号； 3）量化输出信号； 4）编码结果。

2