随机过程理论总结(持续更新)
预备知识:
和差化积:
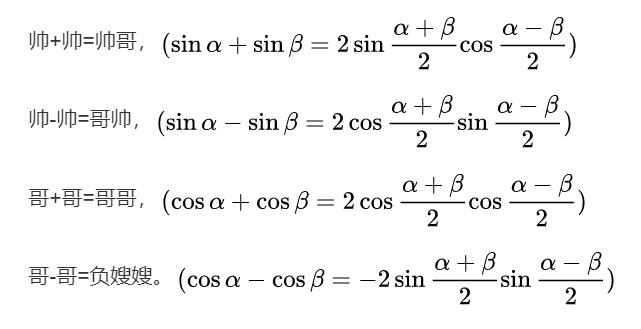
积化和差:
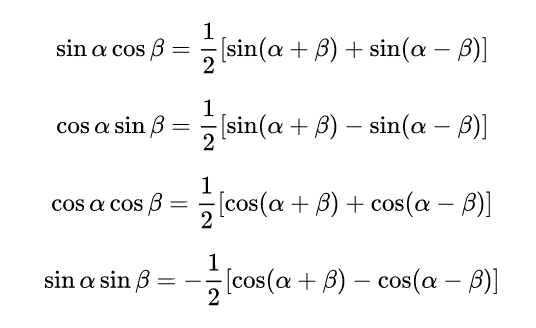
积化和差得和差,余弦在后要相加;异名函数取正弦,正弦相乘取负号。解释:
(1)积化和差最后的结果是和或者差;
(2)若两项相乘,后者为cos项,则积化和差的结果为两项相加;若不是,则结果为两项相减;
(3)若两项相乘,一项为sin,另一项为cos,则积化和差的结果中都是sin项;
(4)若两项相乘,两项均为sin,则积化和差的结果前面取负号。
第一章、概率与随机变量
定义:

统计描述:
一维随机变量:

二维随机变量:

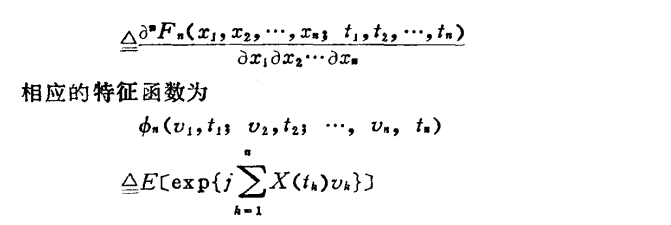
分类:

第二章、随机过程概述
随机过程的数字特征
均值(数学期望):
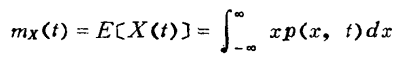
均方值:
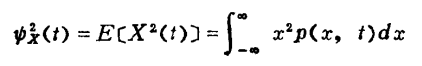
方差:
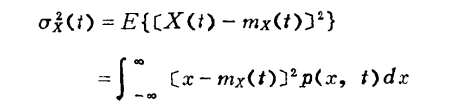
自相关函数:
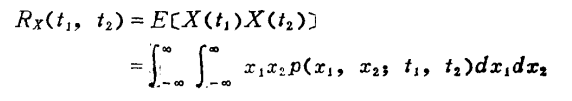
协方差:
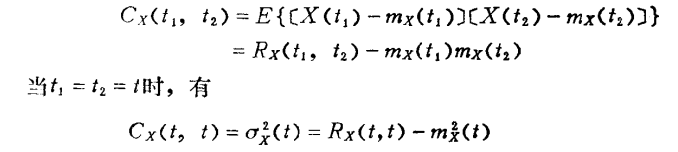
平稳随机过程的数字特征:
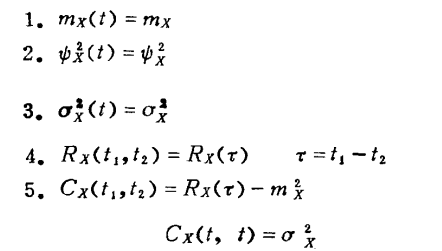
复随机过程的数字特征:
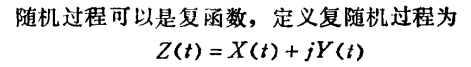
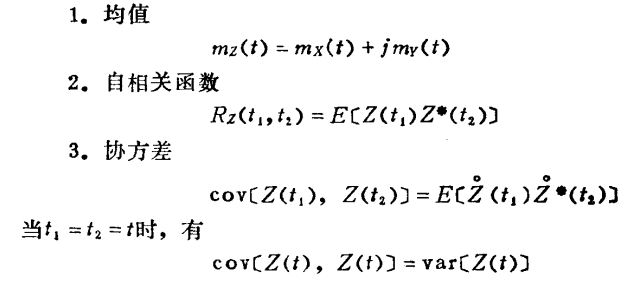
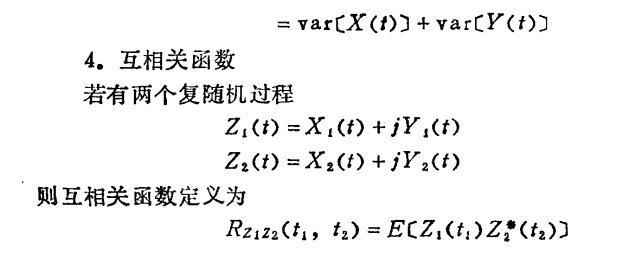
平稳随机过程
严格平稳随机过程:

广义平稳随机过程:

平稳随机过程相关函数 RX(τ) 的性质:
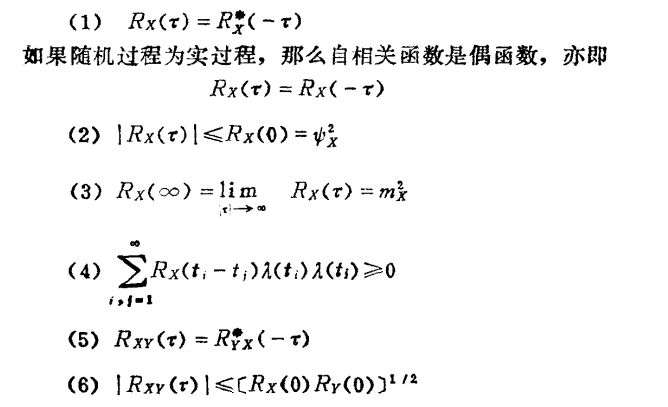
样本函数的时间平均:


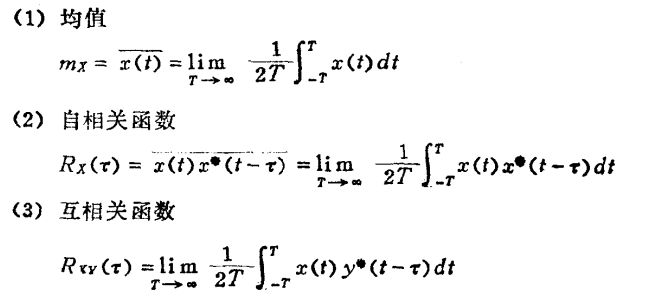
平稳过程的功率谱密度S(w):
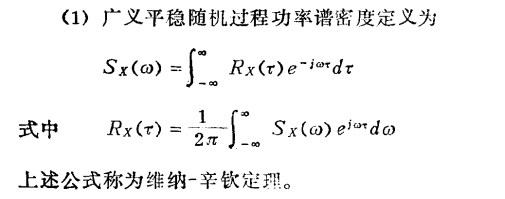
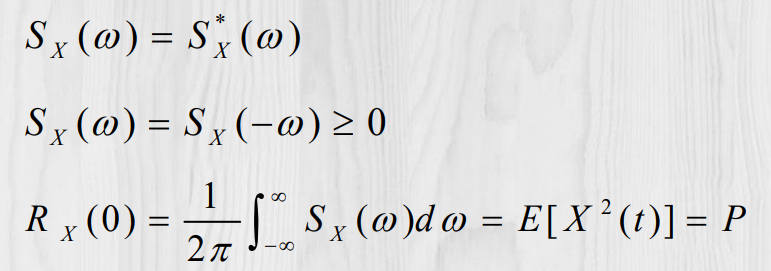

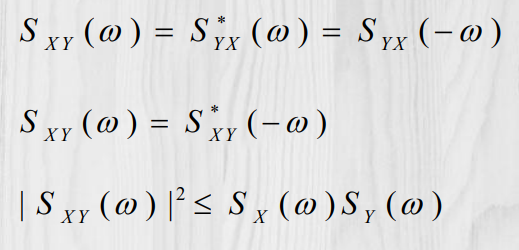
矢量随机过程
例题
由 随机过程 求 随机变量 :


由 随机过程 求 分布函数 :




由 随机过程 求 概率密度 :
例1:

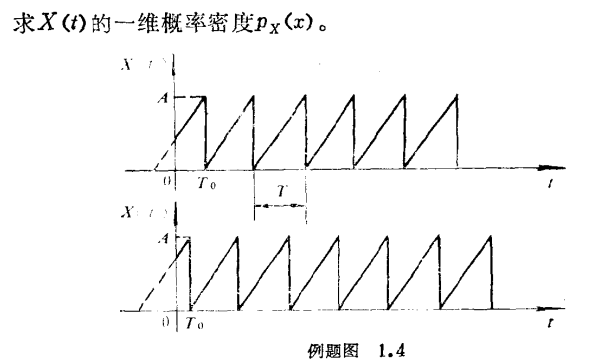
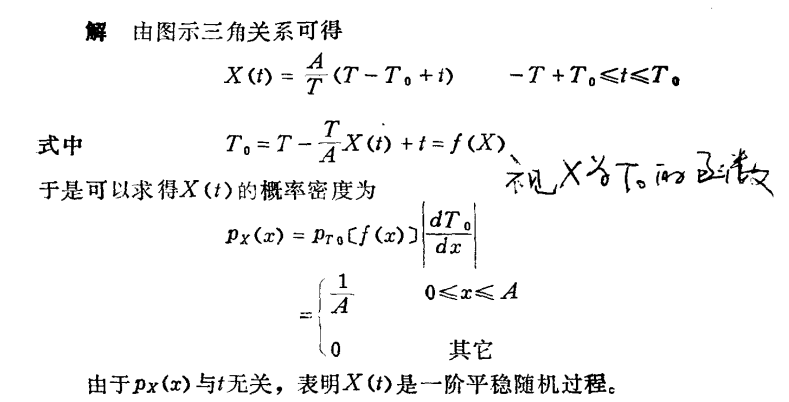
例2:
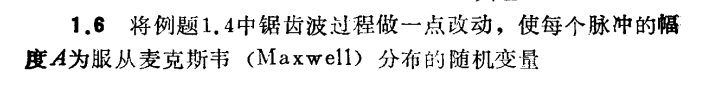
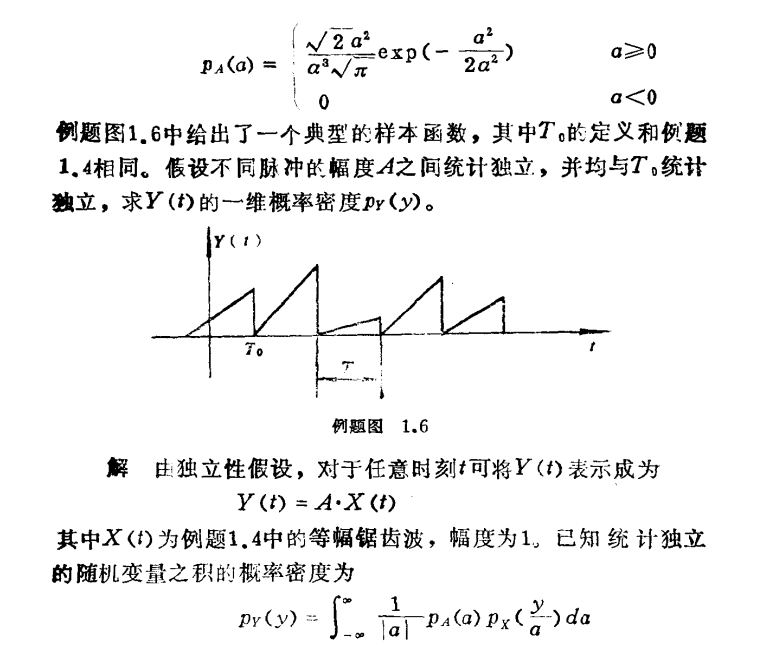
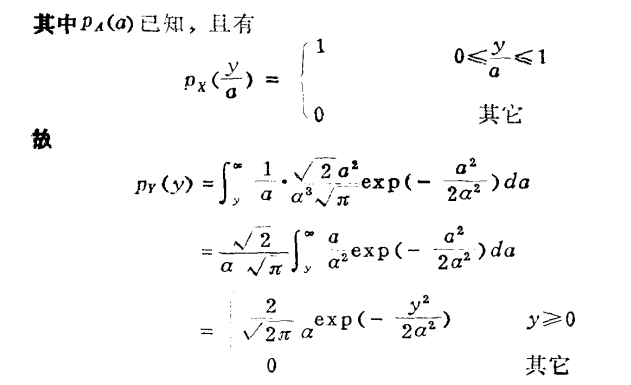

例3:


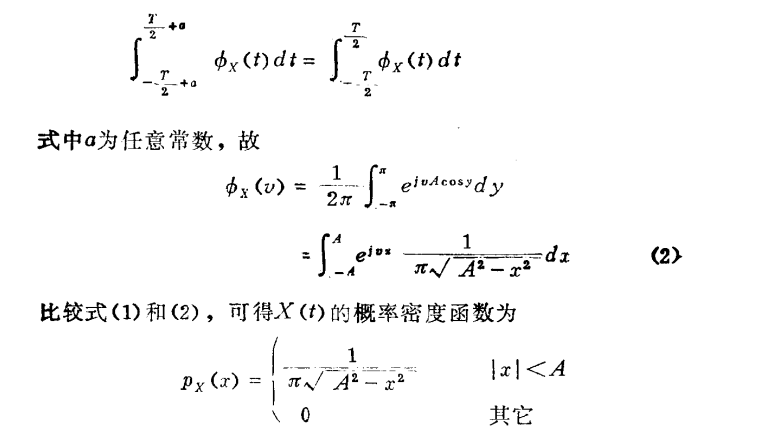
求 随机过程 的 均值函数 和 自相关函数 :


证明 随机过程 是 一阶平稳过程 :



证明 随机过程 是 平稳随机过程 :

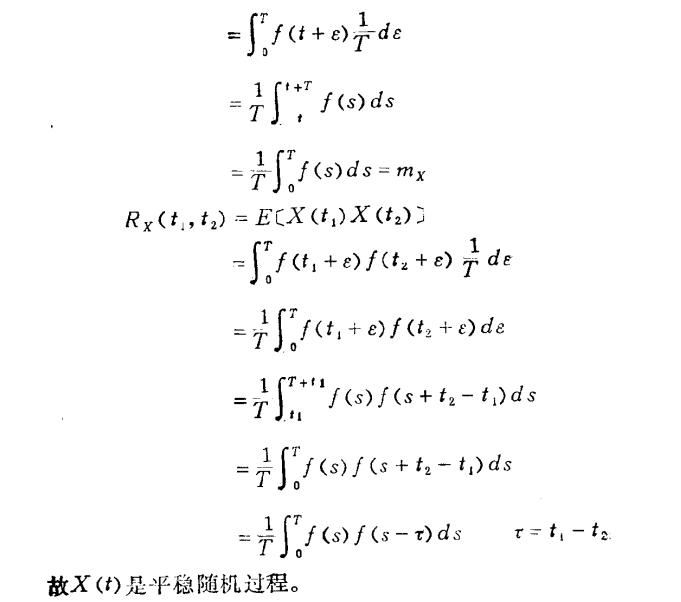
由 随机过程 求 均值、自相关函数、判断平稳 :

由 随机过程 判断 是广义/狭义平稳随机过程 :


证明 是广义平稳过程:

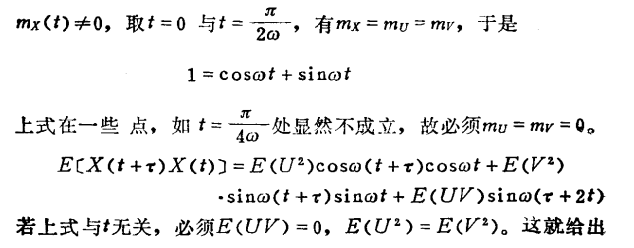
证明 随机过程的均值 是 各态历经的:


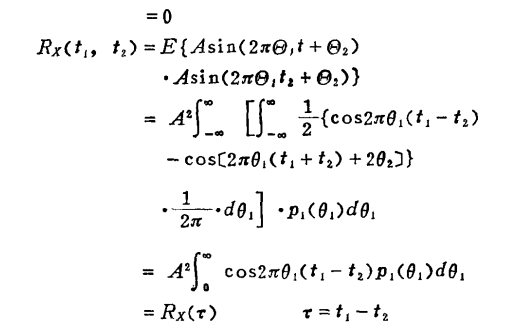
重点看看吧!!!


由 谱密度 求 自相关函数和均方值 :

由平稳随机过程 求 **功率谱 ** :
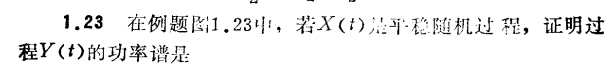
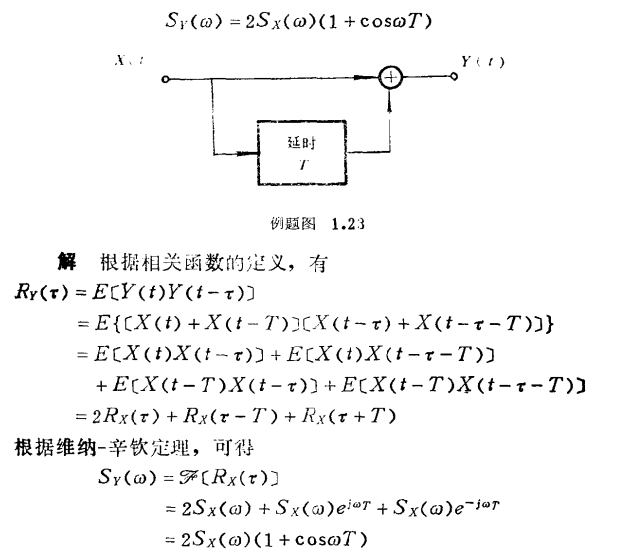
第三章、随机过程的线性变换
随机过程变换的基本概念:
线性系统:

随机过程的收敛性:

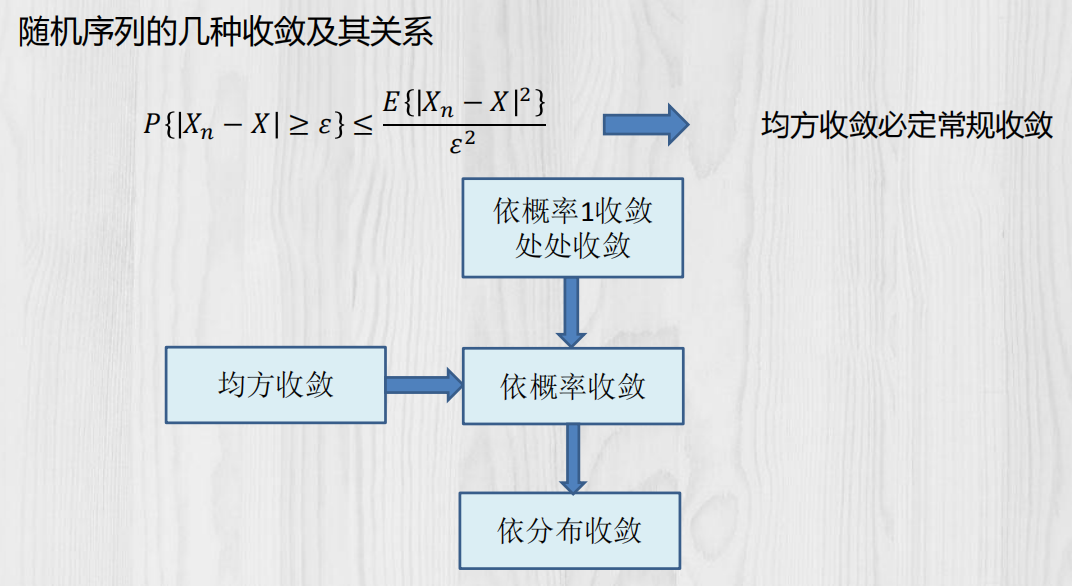
随机过程的均方连续性:

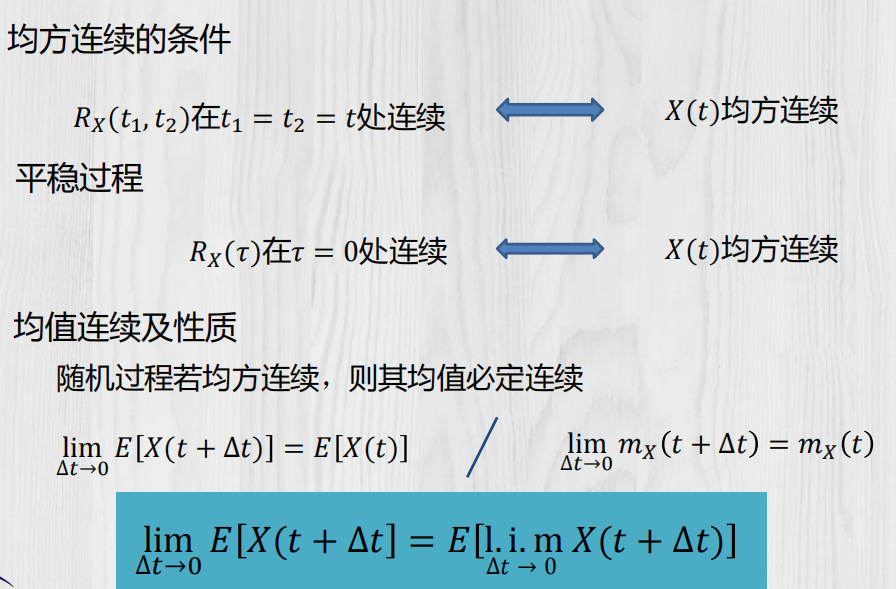
随机过程的均方导数:
均方导数的定义:

均方可微的条件:

均方导数的均值:
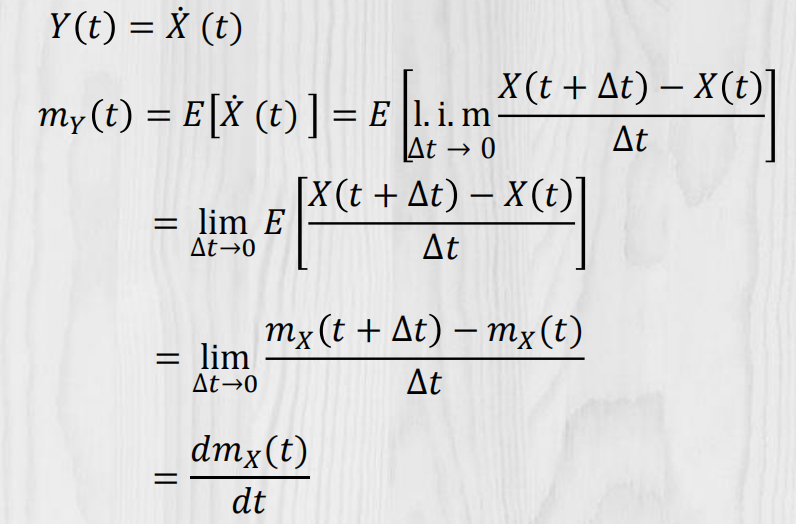

均方导数的相关函数:


可以考虑 τ = t1-t2;在等式后面乘 dτ/dτ;根据以下的方法推算:
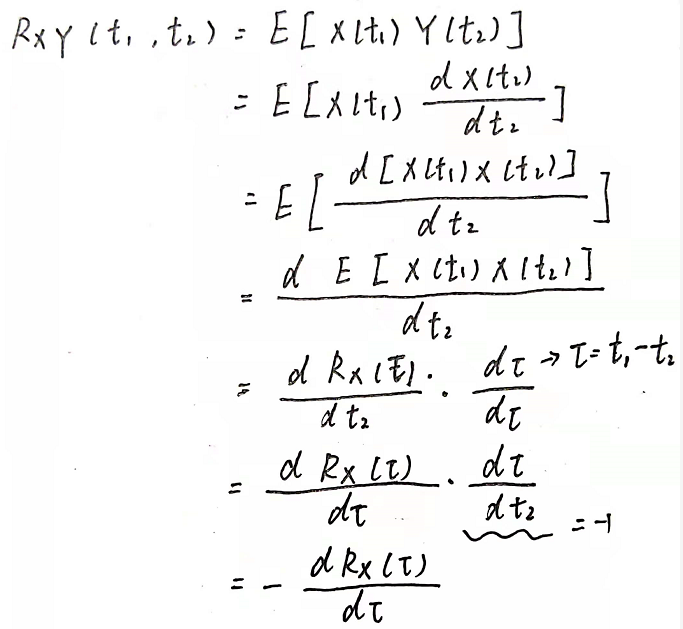
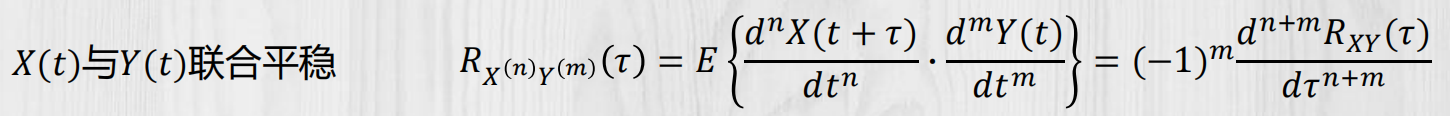
均方导数的功率谱密度:
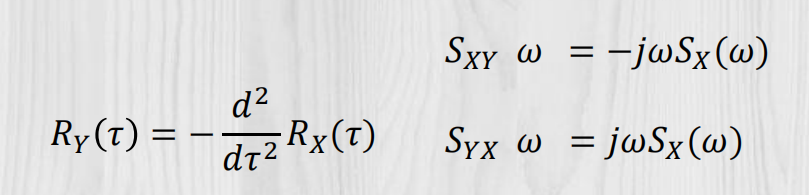
随机过程的均方积分:
均方积分的定义:

均方积分的可积条件:
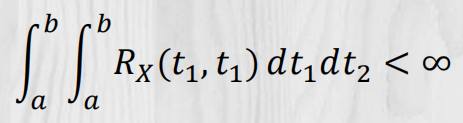
均方积分的性质:
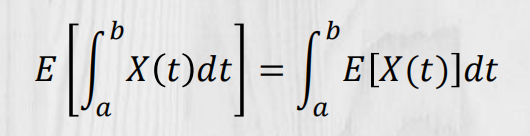
均方积分的积分变换:
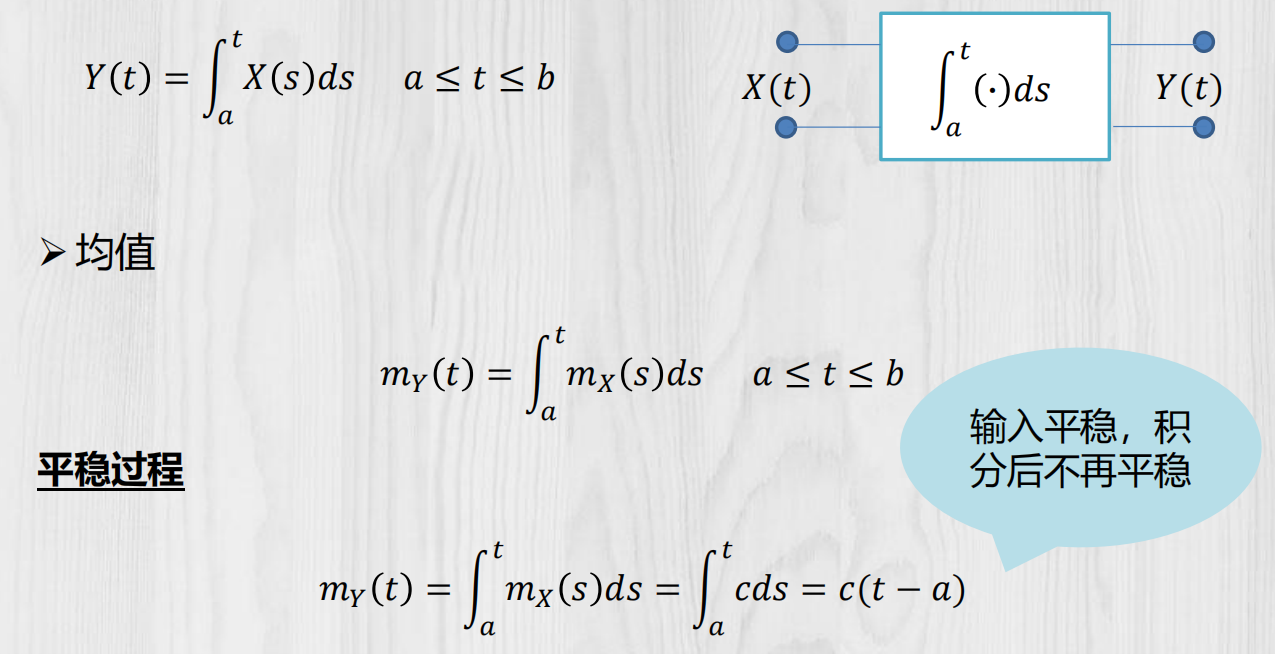
均方积分的相关函数:
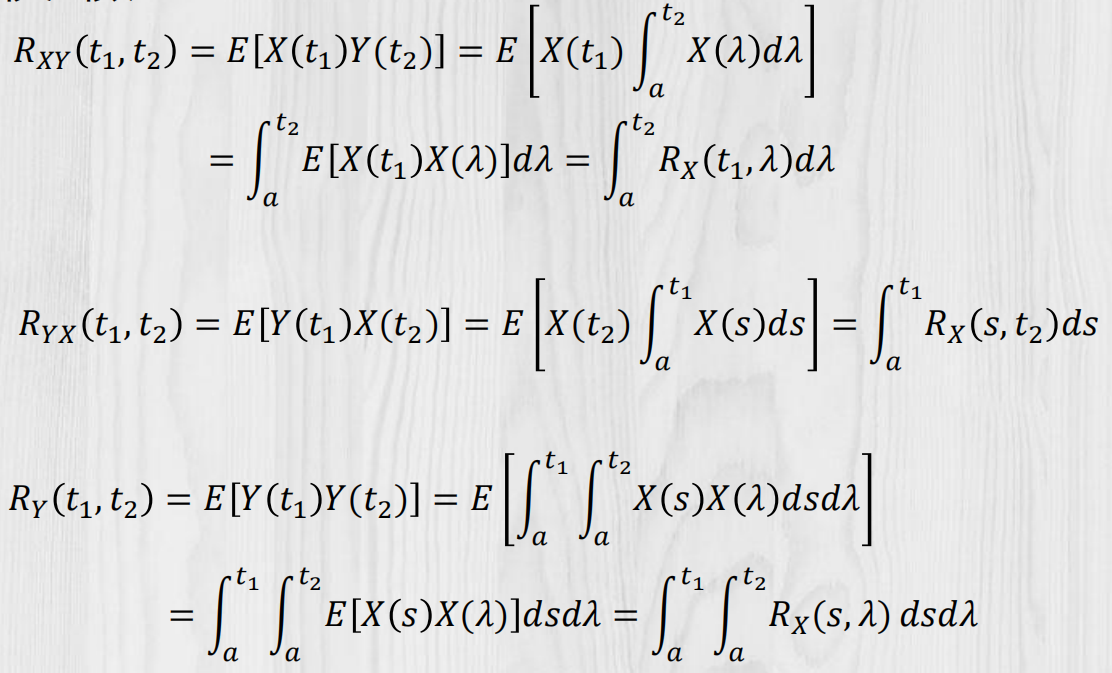
随机过程通过线性系统:
冲激响应法:
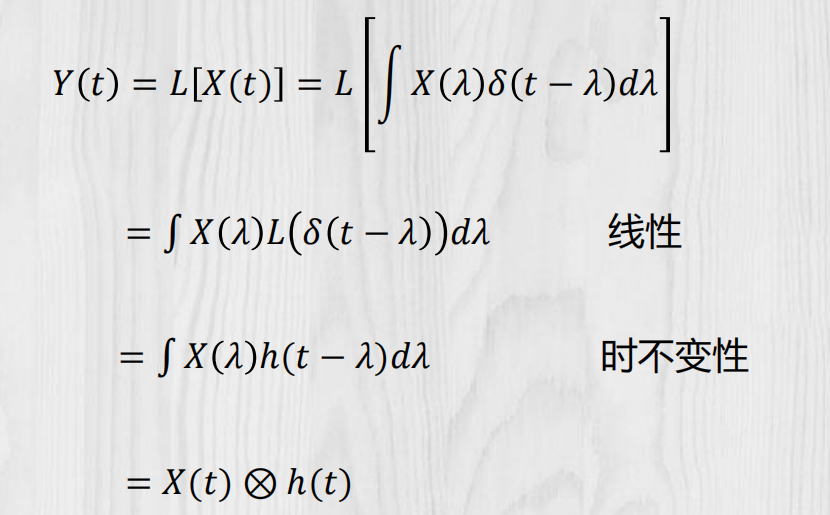
一般随机过程:


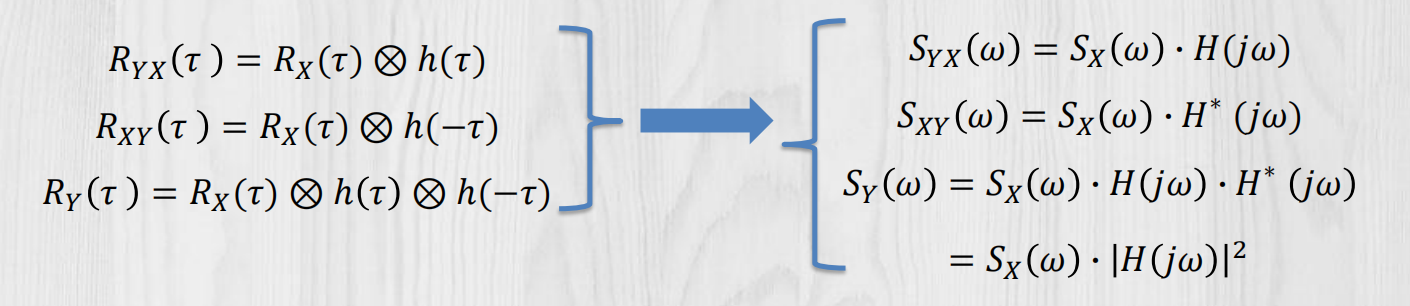
平稳随机过程:


平稳随机过程的频谱分析法:
白噪声通过线性系统:
频谱法:
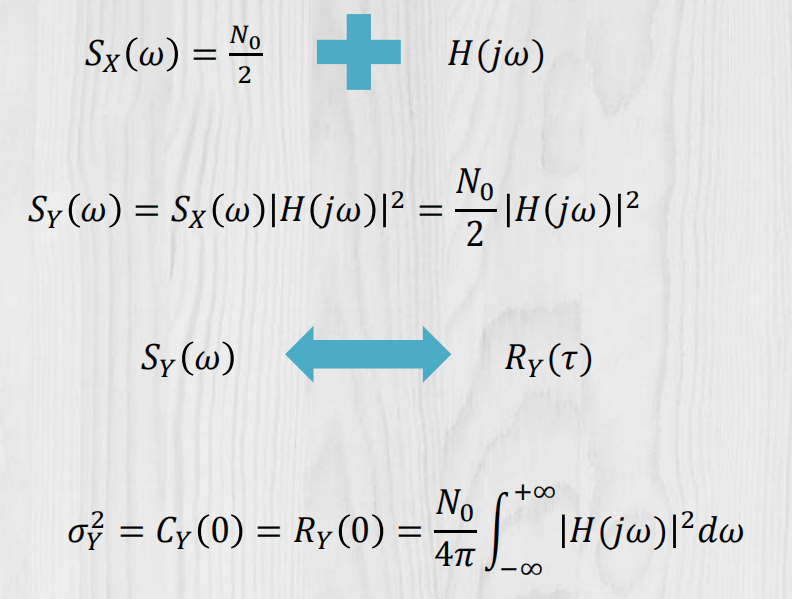
冲激响应法:
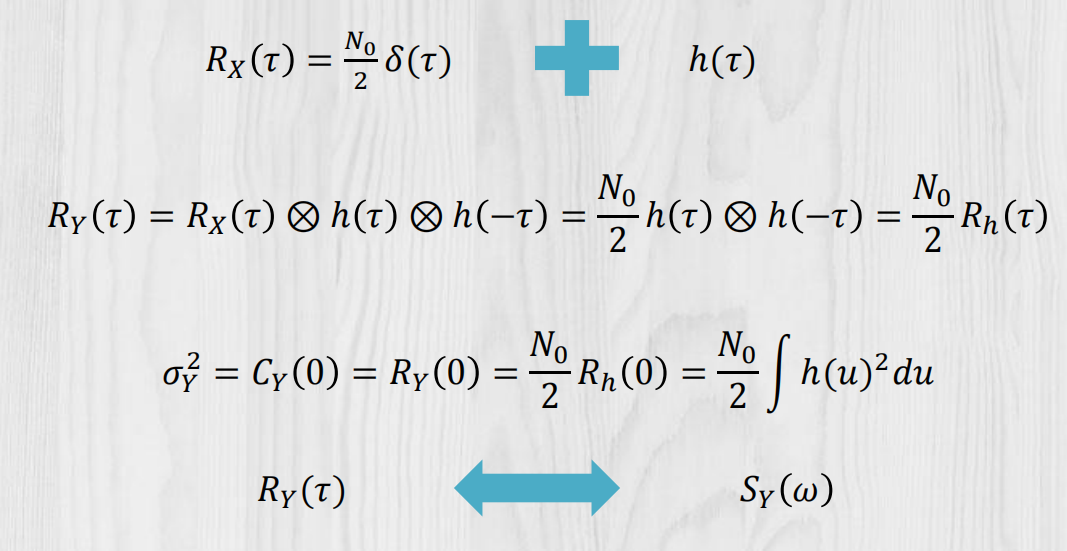
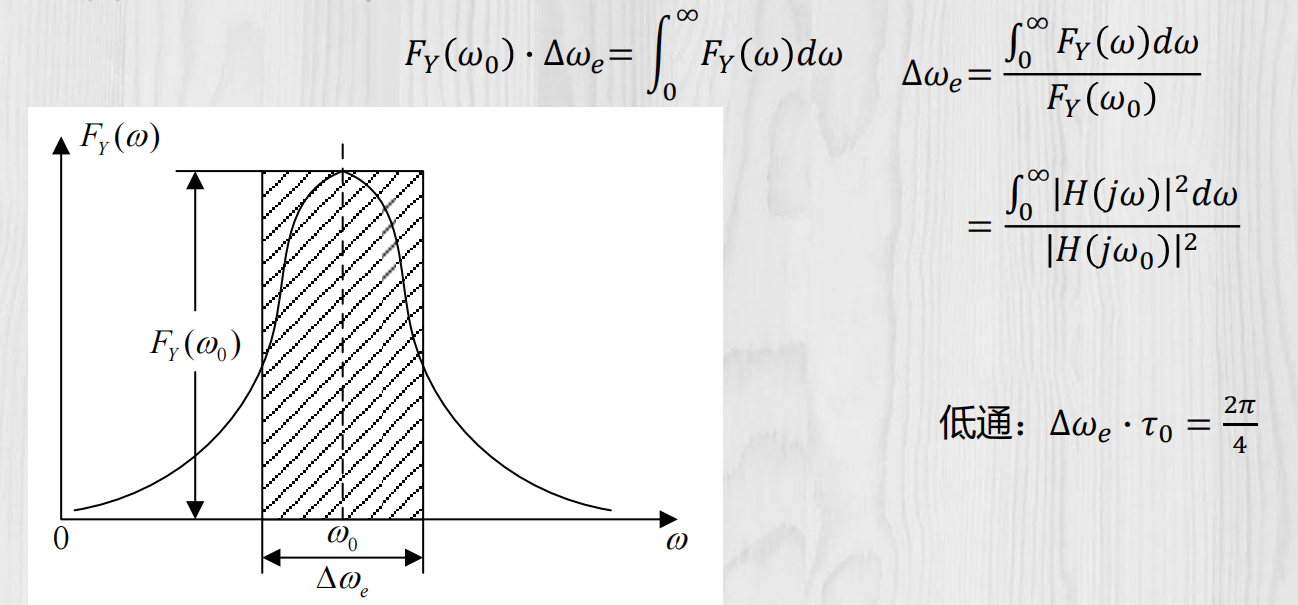
噪声等效通频带:
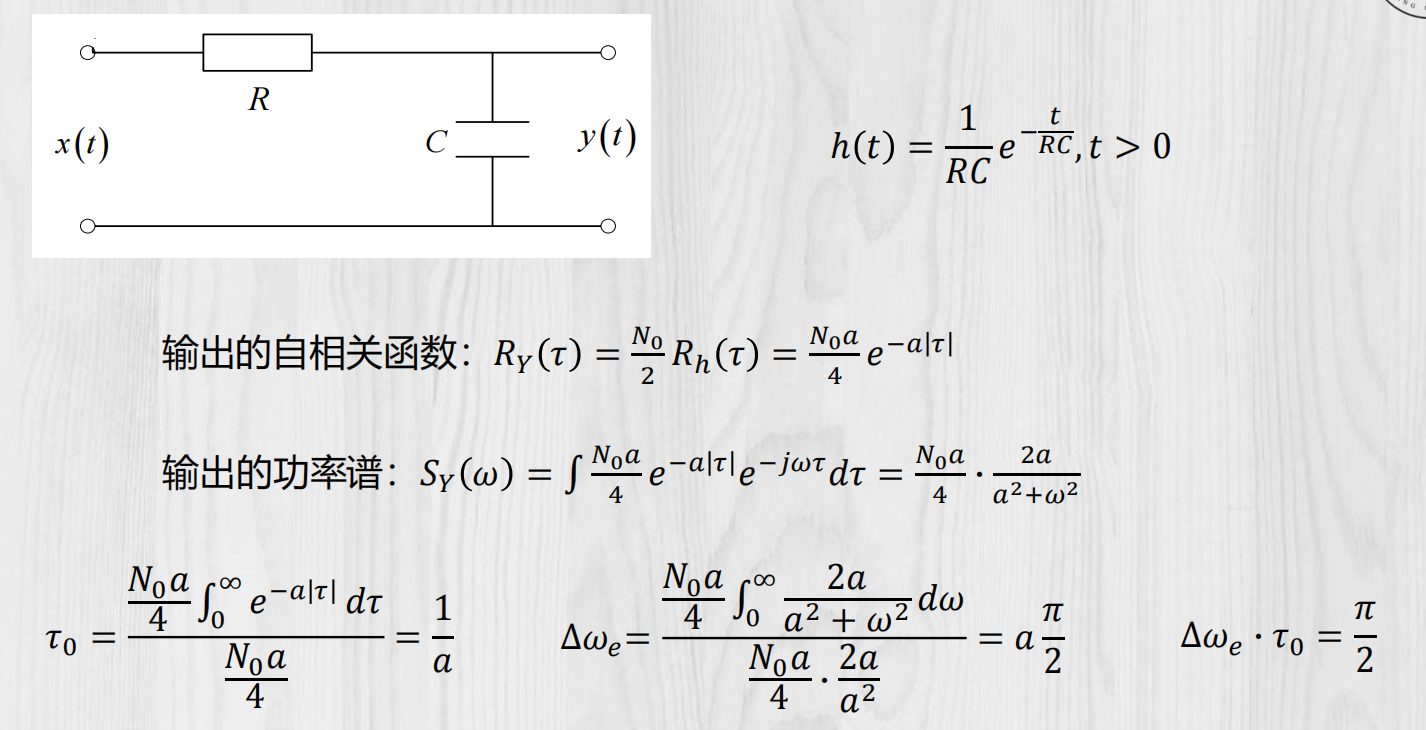
白噪声通过RC积分器:
第四章、窄带随机过程
确定性信号的复表示:
1. 余弦信号的复信号表示
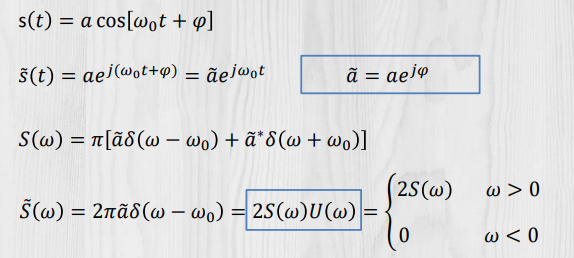
• 复表示能够给出相位信息
• 其频谱只在正频域存在,具有单边谱
2. 窄带信号的复信号表示
窄带信号:𝑓0 ≫ ∆𝑓

3. 任意信号的复表示
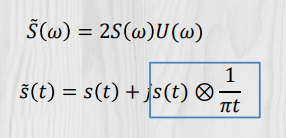
希尔伯特变换:
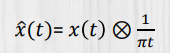
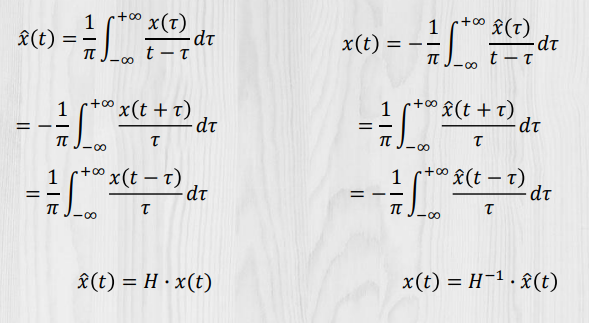

对于有限带宽信号
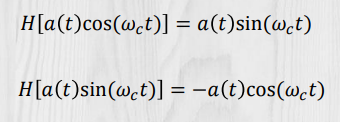
实随机过程的复表示

窄带过程定义及其同相、正交分量
nc -> 同相分量
ns -> 正交分量
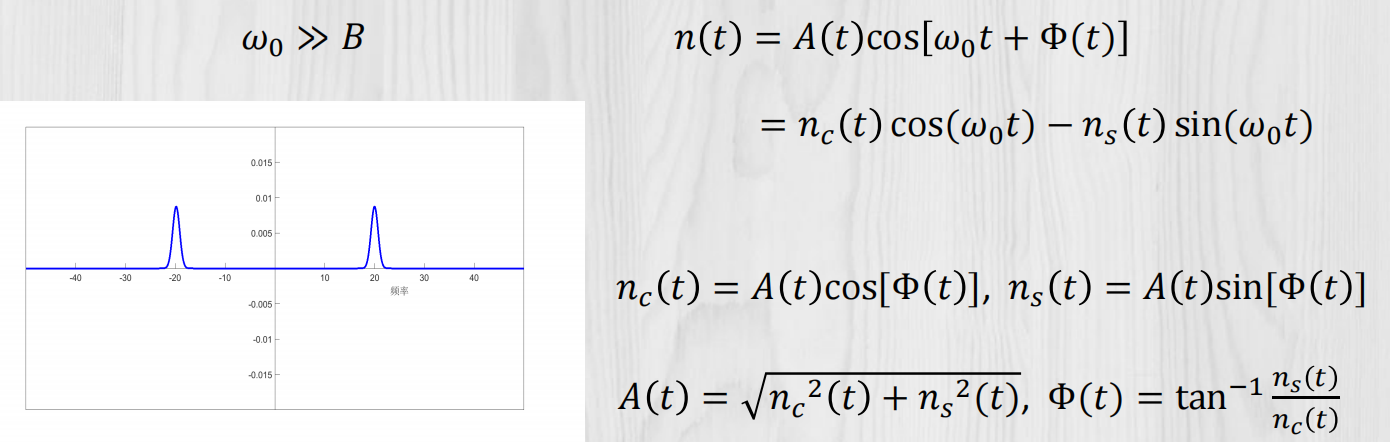
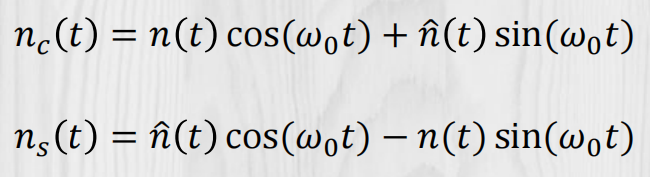
自相关函数:
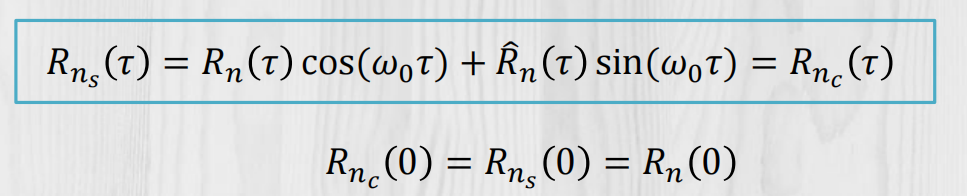
互相关函数:
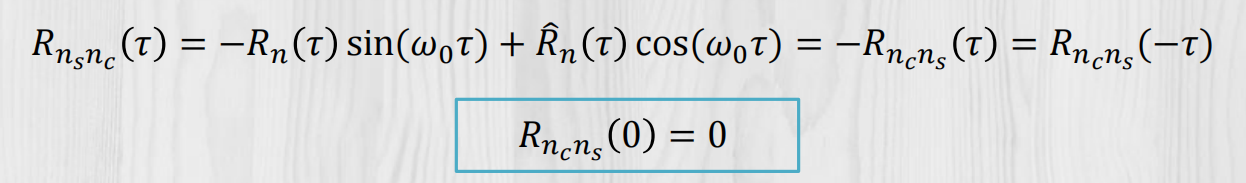
规律谱:
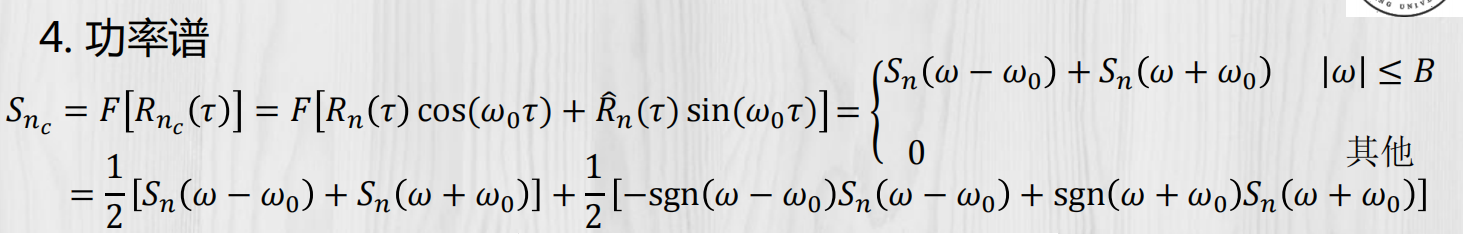
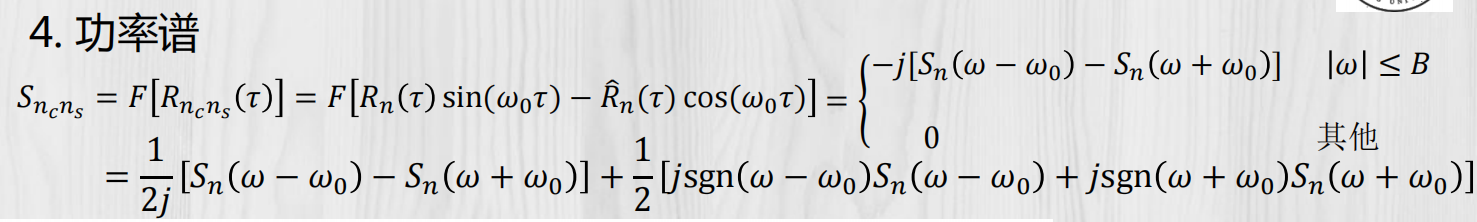
本博客所有文章除特别声明外,均采用 CC BY-NC-SA 4.0 许可协议。转载请注明来自 52_Hertz!
评论