数电ModelSim作业3
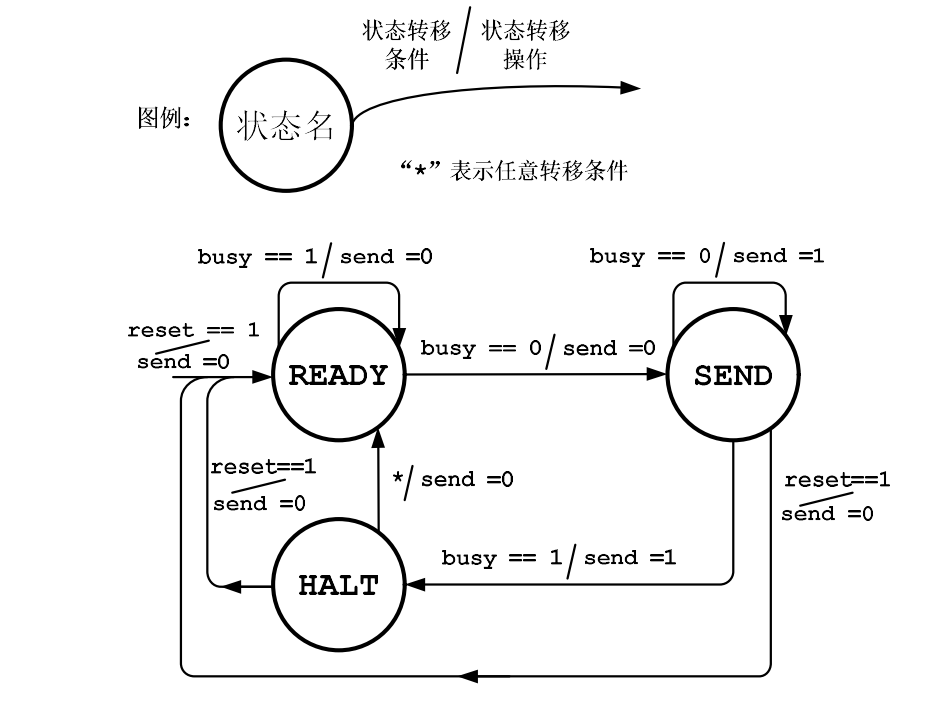
数电ModelSim作业3请实现如图所示的有限状态机,具体要求为:
请完成状态机的模块实现,并编写测试程序,分别测试 “READY->SEND->HALT->READY” 和 “READY->SEND->READY” 两条典型的状态转移路径。(请给出模块实现、测试代码和功能仿真结果)
一、新建Project具体可以参考 “数电ModelSim作业1”
二、程序代码12345678910111213141516171819202122232425262728293031323334353637383940414243module tx_FSM (clock, reset, busy, send); parameter [1:0] READY = 2'b00, SEND = 2'b11, HALT = 2'b10 ; input clock ; input reset, busy ; output send ; reg [1:0] state, next_state ; always @( posed ...
数电ModelSim作业2
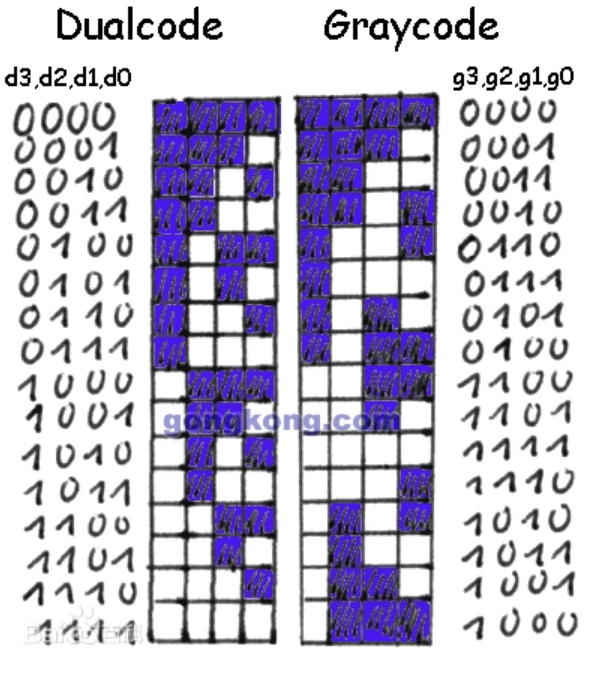
数电ModelSim作业2自然二进制码 转换为 格雷码一、新建Project具体可以参考 “数电ModelSim作业1”
二、程序代码自然二进制码:二进制:以2为基数的记数系统
格雷码:在一组数的编码中,任意两个相邻的代码只有一位二进制数不同
实现原理( 自然二进制转换成格雷码 ):
二进制码转换成二进制格雷码,其法则是:
1、保留二进制码的最高位作为格雷码的最高位
2、格雷码其余各位为二进制码这一位与二进制码高一位异或。
代码如下:
12345678910module Bin_to_Gray #( parameter NUM = 8 ) ( input [ NUM-1 : 0 ] bin , output [ NUM-1 : 0 ] gray ) ; genvar i ; assign gray[NUM-1] = bin[NUM-1]; generate for (i = 0; i < NUM-2; i = i+1) beg ...
数电ModelSim作业1
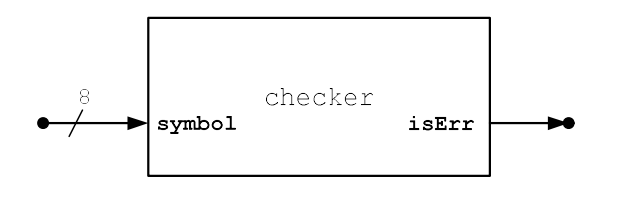
数电ModelSim作业1 设某符号 Symbol 由 7 位信息码元和 1 位校验位组成,采用奇校验,即:发送端通过对校验位赋值,使符号中 “1” 的数目为奇数;如果符号在传输过程中受到干扰,有的码元可能发生翻转。
请用 Verilog HDL 语言设计一个奇校验检查电路,根据接收到符号中“1”的数目,判定该符号是否错误;请写出完整的模块。(设:该符号并行输入到接收端,电路的输入输出接口如图所示。)请用 Modelsim(或其它 EDA 编译/仿真器)实现模块、测试代码和功能仿真结果。
1、建立library在建立工程(project)前,需要先建立工作库(library),一般命名为“work”,以后建立的所有project都在“work”下面工作。
1File -> new -> Library -> a new library -> 命名为“work”
此时在Library中加入名为“work(empty)”的工作库。
2、建立project和新文件1File -> new -> Project ...
电子电路2实验CAD4-435
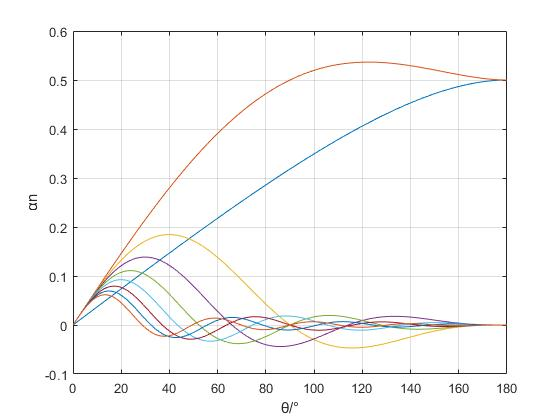
CAD-44-35 利用MATLAB程序和尖顶余弦脉冲的分解公式,画出尖顶余弦脉冲分解系数图。尖顶余弦脉冲的分解公式:
一、MATLAB程序123456789101112131415161718t = 0:0.001*pi:pi; n = 9;A = zeros(n,1001);rad = t;A(1,:) = (sin(t)-t.*cos(t))/pi./(1-cos(t));A(2,:) = (t-sin(t).*cos(t))/pi./(1-cos(t));for i = 3:n A(i,:) = 2*(sin(i*t).*cos(t)-i*cos(i*t).* sin(t))/i/pi./(i*i-1)./(1-cos(t));endrad = t/pi*180;for i = 1:n plot(rad,A(i,:)); hold on;endgrid on;xlabel('θ/°');ylabel('αn');
二、程序运行结果
电子电路2实验CAD3-322
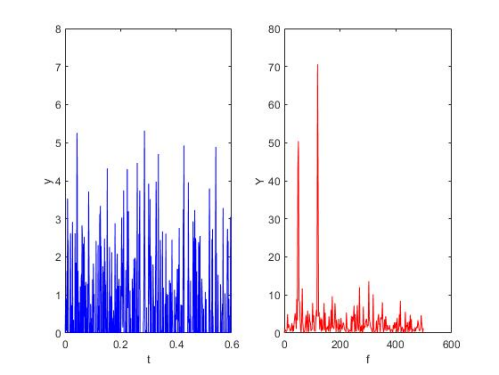
CAD3考虑一个被噪声污染的信号,很难看出它所包含的频率分量。应用Matlab 中的傅立叶变换可以在噪声中发现淹没在其中的信号。Y = fft(X,n)即是采用n 点的FFT变换。
3-22 考虑一个被噪声污染的信号,很难看出它所包含的频率分量。应用Matlab 中的傅立叶变换可以在噪声中发现淹没在其中的信号。Y = fft(X,n)即是采用n 点的FFT变换。
举例:一个由50MHz和120MHz正弦信号构成的信号,受零均值随机噪声的干扰,数据采样率为1000Hz。现可通过fft函数来分析其信号频率成份。
参考程序:
t=0:0.001:0.6;
X=sin(2pi50t)+sin(2pi120t);
y=X+1.5*randn(1,length(t));
Y=fft(y,512);
P=Y .*conj(Y)/512;
f=1000*(0:255)/512;
plot(f,P(1:256))
这样可得到信号功率谱密度图。
一、MATLAB程序MATLAB程序代码如下:
12345678910111213141516t=0:0.001:0.6; X=sin(2*p ...
电子电路2实验CAD2-317
CAD23-17 题图 1所示为单管共射极放大电路的原理图。设晶体管的参数为:
,,,,。调节偏置电压使。用 PSpice 程序求解:
(1)计算电路的上限频率和增益-带宽积;
(2)将改为200Ω,其他参数不变,重复(1)的计算;
(3)将改为1KΩ,其他参数不变,重复(1)的计算;
(4)将改为9pF,其他参数不变,重复(1)的计算;
(5)将从400MHz改为800MHz,其他参数不变,重复(1)的计算;
根据上述结果讨论、、、对高频特性的影响。
图 1 共发射极放大电路原理图
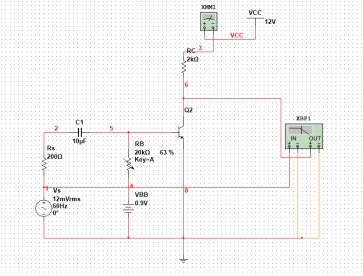
一、Multisim仿真电路(1)计算电路的上限频率和增益-带宽积仿真电路如图 2 所示:
图 2 Multisim仿真电路
计算题目所给参数计算:
对三极管参数的以下参数进行调整,如图 3:
图 3 三极管需要调整的参数及其数值
观察波特仪输出得到电路的幅频特性,如图4,其最高增益为,,,得增益带宽积
图 4 原始幅频特性曲线
(2)将改为200Ω,其他参数不变,重复(1)的计算观察波特仪输出得到电路的幅频特性,如图5,其最高增益为,,,得增益带宽积
图 5 改为200Ω幅频特性 ...
电子电路2实验CAD1-211
CAD12-12 用有源RC电路实现习题2-11所得低通滤波器,并用PSpice程序分析其中所用运算放大器的参数对滤波器频率特性的影响,这些参数包括:
(1)输入与输出电阻;
(2)增益;
(3)频率特性(只考虑单极点运算放大器)。
请对分析结果作简单说明。
2-11 请用巴特沃斯逼近方法设计一个低通滤波器,要求在频率0~3kHz范围内衰减小于2dB,频率高于30kHz的范围频率衰减大于35dB,信源与负载阻抗为600Ω。
经计算,滤波器为一阶,具体参数如下:
一、设计电路由 2-11 计算得 n = 2 , C1 = 112.54nF , L2 = 40.514mH , 绘制Butterworth滤波器,如 图 1 所示:
图 1 2-11 题Butterworth滤波器结构及参数
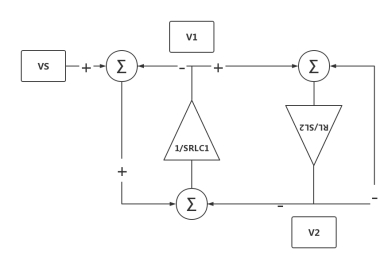
将以上的LC低通滤波器改为有源RC电路,功能框图如 图 2 所示。
图 2 功能框图
对上图列节点电压方程:
解得:
又因为:
所以可以画出有源RC低通滤波器电路,如 图 3 所示:
图 3 有源RC低通滤波器
二、Multisim仿真电路1、使用Multisim的运算放大器LM3 ...
BUAA期末《概率统计》复习大纲
概统复习大纲题型123456789填空:40分 8*5计算(最好先把公式写上,公式写对有分,尽量写分数不写小数,如果写小数保留2位)问答 如分布类型,公式系数等概念题证明:10分考点:大数定律,概率收敛,概率体系,性质计算:50分课后习题类型每章一道
总结第一章概率的公理化体系:
12设S是样本空间,F 是 S 的某些⼦集构成的集合类,若 该集合类对交并补运算封闭,则这些⼦集都可以视为是 随机事件,因此可以称 F 为试验E的 “事件域”。考点:计算概率(古典概率,几何概率)
四大公式:加法公式,乘法公式,全概率公式,贝叶斯公式
第二章12345678910随机变量的分布分布函数,概率密度,分布列的性质熟悉具体分布是什么以及使用背景重点:分布的期望,方差,概率两点分布,二项分布,泊松分布均匀分布,指数分布,正态分布分布的函数计算
第三章1234联合分布,边缘分布,条件分布(关系)Z=g(X+Y)重点:和分布,最小值最大值(n个变量)多重积分:积分限的确认
第四章1234567891011121314收敛:1.依概率收敛和依分布收敛(重点)2.极限运算法则3.依分布 ...
BUAA期末《电子电路1》复习大纲
电子电路复习大纲第一章:重点公式:
第二章:推挽输出
1234567891011121314151617交越失真:输入信号 ui 在过零前后时,输出信号出现的失真。乙类: 每管BE结正偏时间约等于半个周期特点:由NPN型、PNP型三极管构成两个对称的射极输出器对接而成 双电源供电 输入输出端不加隔直电容 Pomax = 2Vcc2/2RLPEmax = 2Vcc2/πRL最大平均电流:I = Vcc/πRL最大效率: pi/4 = 78.5
第三章:波特图画法:
1234567891011121314151617频率响应:电压增益与频率有关 频率失真:对输入信号的各次谐波的放大倍数不同 相位失真:对输入信号各次谐波的相移不成比例 常数项:Av(0)一阶零点因子:向上:+20dB/十倍频、0°-90° 幅频:wz:3dB 相频:0.1wz:0.72° 一阶极点因子:与零点关于x轴对称# 零点为0,没有误差,相频过(1,0),幅频恒等于+9 ...