信号与系统复习大纲

第一章 概论

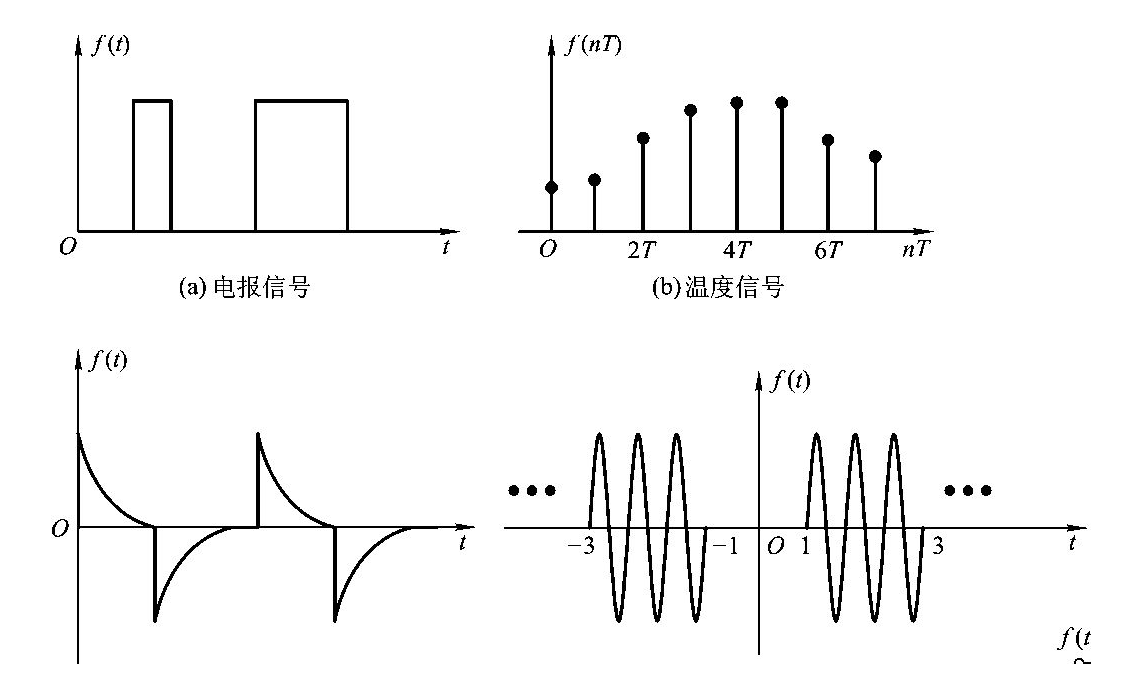
信号的分类：确定性\随机性、连续时间\离散时间、周期\非周期、能量有限\功率有限

1
2
3
能量有限信号：在T趋向无穷，从-T/2到T/2 对 f(t)^2 进行积分，结果有限

功率有限信号：在T趋向无穷，从-T/2到T/2 对 f(t)^2 进行积分后除 T ，结果有限

信号的运算

1
2
3
4
5
倍乘运算、微积分、四则运算

反褶运算、时移运算、压缩与扩展

方法：宗量函数不变法

基本信号

1
2
3
4
5
6
7
8
9
指数类信号：指数信号、正余弦信号

奇异信号：单位斜变信号、单位阶跃信号、单位冲激信号
	（
	  时移运算：
	  反褶运算：
	  压扩运算：
	  微分运算：**p23**
	 ）

线性时不变系统

1
2
3
4
5
叠加性、均匀性

（先线性再叠加） == （先叠加再线性） ？

（先时移再过系统） == （先过系统再时移） ？

信号类型的判断及运算

1
可逆系统：激励与响应一一对应

​ 无记忆系统 与 因果系统 的区别：

1
2
3
无记忆系统：只取决于当前这一刻的时间

因果系统：可以取决于之前的所有，只是不能依据这一时刻后的

​ 稳定\不稳定系统：

1
激励能量有限，响应能量也有限

系统特性的判断

1
2
3
4
5
线性：y和x及其各阶导数不存在平方关系
时不变：t前面没有符号、没有系数、没有平方
有记忆：t都是一直单独存在
因果：只有t和t+T0存在
稳定：没有 1/t、ln t 之类

第二章 连续系统 - 时域

求系统响应

​ 自由响应 / 强迫响应

1
自由响应：齐次解；Ci 由 y（0+） 决定强迫响应：特解+激励； Ci 由 比较系数得出

​ 零状态 / 零输入相应

1
零输入响应：齐次解； Ci 由 y（0-）决定零状态响应：齐次解+特解；Ci 由 y（0-）=0 ， 求出的 y（0+）确定

​ 暂态 / 稳态响应

1
暂态响应：全响应中随时间衰减的部分稳态响应：全响应中一直存在的部分

单位冲击响应

​ 冲激信号会使起始状态发生跳变（电容两端加电压、电感两端加电流）

​ 单位冲击信号作用于系统的零状态响应

起始点的跳变

​ 左侧最高次等于右侧最高次，然后积分，det u(t) 前面的系数就是跳变量

卷积的定义与计算

$$
s(t)=x(t)*y(t)=∫x(τ)y(t-τ)dτ
$$

1
2
3
4
5
性质：

1、微积分性质 **p59**  			**f1微分的积分等于他自己**	

2、δ(t)的卷积性质

LTI系统

1
2
3
因果性： h（t）= h（t）u（t）

稳定性： h（t）绝对可积

第三章 连续信号 - 实频域

基于信号自身的正交分解

​ 直流分量+交流分量

​ 奇分量+偶分量

基于 e^jwt^ 的正交分解 ( 满足狄利克雷条件、f（t）绝对可积 )

周期函数——傅里叶级数

1
2
3
4
5
单边频谱 与 双边频谱：	

幅度谱：双边与单边在 w=0 处幅度相同，else双边的幅度是单边的一半	

相位谱：双边谱是单边谱关于原点对称的
1
奇谐函数：奇次谐波偶谐函数：偶次谐波

非周期函数——傅里叶变换（线性变换）

傅里叶变换 与 傅里叶级数 的关系：
$$
F(nw1)=1/T1 * F1(w) | w=nw1
$$

傅里叶变换的性质

1
实偶函数 -> 实偶函数实奇函数 -> 虚奇函数

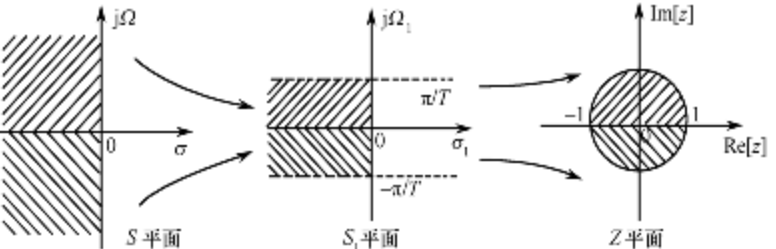
时域抽样定理

信号带宽

​ 截止频率 wc ：有限带宽wm 、3dB带宽、零点带宽、等效带宽

抽样定理

​ ws >= 2wm （wm 为截止频率）

信号的恢复

​ 通过w=wc 的低通滤波器

第四章 连续系统 - 实频域

系统频响 H(w) （ h（t）的傅里叶变换变换）

1
特例：	激励为正余弦信号，通过 H（w），幅度受到 |H（w1）|的加权，相位发生了ψ（w1）的相移。

无失真传输

1
2
3
4
5
r(t)=ke(t-t0)条件判断：
幅频：|H(w)=k|；为k，是常数		
相频: ψ(w)=-wt0; 斜率小于0的斜直线		
幅度失真：E1/E2 ！= R1/R2   
E、R表示输入和输出信号的幅度相位失真：ψ（w1）/ ψ（w2）！= w1 / w2

理想低通滤波器

H(w) = e^-jwt0^ , |w| < wc 

1
2
3
理想低通滤波器的单位冲激响应：单位冲激响应 h（t）=wc/pi * Sa[wc(t-t0)]

理想低通滤波器的单位阶跃响应：理想低通滤波器对矩形脉冲的响应：

上升时间 tτ = 2pi / wc

系统的因果性（系统物理可实现）

佩利-维纳准则

希尔伯特变换

相关函数与卷积 R12 = f1（τ）* f2（ - t）

能量谱和功率谱

1
2
3
能量谱与功率谱的计算：	自相关函数 R（τ）与能量谱|F（w）|^2 构成傅里叶变换对		

功率谱函数|F（w）|^2 与 自相关函数 R（τ）构成傅里叶变换对

信号的恢复：p182

调制与解调系统

1
调制：	幅度	同步解调

第五章 连续信号与系统 - 复频域

拉普拉斯变换、逆变换

收敛域、性质、初值定理、终值定理

逆变换：部分分式分解

收敛域：双边信号的拉普拉斯变换

应用拉普拉斯变换求系统响应

已知0-

1
零状态响应，0-的值全部为0，只剩有 H（s）的项，移项相除分离出 H（s），逆变换得到h（t）

已知0+

1
不能考虑δ(t)，右侧激励全部换成0，左侧代入 H（s）、s和常数项，再整理得出 H（s）

系统函数（ h（t）的拉普拉斯变换）

​ 把频率响应 H（w）中的 jw 换成 s

1
2
3
级联：上一级输出 作为 下一级输入 ，系统函数 等于 两个子系统函数的 乘积

并联：输入相同、总的输出，系统函数 等于 两个子系统函数 之和反馈：H1 / （1 + H1*H2 ）

零 zj 极 pi 点分布与时域特性的关系

1
2
3
4
R = E H其中 来自于 H 的极点由系统本身决定，对应齐次解，自由响应	
来自于 E 的极点由激励绝地，对应特解，强迫响应		

位于 s 左半平面 的是衰减信号	位于 s 右半平面和虚轴 的是非衰减信号

系统的稳定性判断

1
2
3
4
5
6
7
H (s) 的极点位于 s 左半平面 or 虚轴上存在一阶共轭极点（边界稳定）分子阶数 <= 分母阶数，系统稳定分子阶数 == 分母阶数 + 1，系统临界稳定分子阶数 > 分母阶数 + 1

系统不稳定稳定性的必要条件：
1、分母多项式 所有系数 全正或全负
2、分母多项式 不缺项 或 缺全部奇次项 或 缺全部偶次项

不同时满足上两种判断方式一定不稳定、同时满足也不一定稳定

劳斯准则

1
n 次多项式 需要列出 （n+1）行前两行上下 从高次项到低次项 写出系数，不够0来补充补充完整若第一列符号相同 —— 稳定	   符号不同 —— 变化次数 = 实根个数

复频域 H（s） 与 频域 H（w）结合

1
2
3
4
5
6
7
8
9
通过系统函数画出幅频特性、相频特性：	
1、在图上画出零极点	
2、w 从 0-∞ ， 从零点沿着y轴正方向到无穷远	
3、找到关键点（每个零极点的虚部）	
4、代入关键点求值全通系统（全通网络）：	
幅频特性为常数的 稳定系统 	
特点：零极个数相同、左右对称（极点在左、零点在右）最小相移系统：	
特点：零极点全在左半平面和虚轴		
在所有幅频特性胸痛的稳定系统中，最小相移系统的相位变化最小

一般系统 = 全通系统 + 最小相移系统

第六章 离散信号与系统 - 时域

线性时不变离散系统及其差分方程描述

1
δ（n） = u（n）- u（n-1）	正弦序列是周期序列  ——   2pi/w 为有理数
1
2
3
4
5
6
7
8
9
10
11
12
13
由差分方程求 全 / 零输入 / 零状态 响应：全响应：	
1、求出齐次解	2、设特解，代入求出特解	
2、通过 -1、-2 求出 0、1 的值	
3、代入齐次解和特解，代入0、1的值，求出全响应	

零输入：	
1、求出齐次解	
2、代入 负时间 的值	

零状态：	
1、求出齐次解	
2、设出特解、并代入求解	
3、零负时间为 0 ，求出正时间，代入求出零状态

单位样值响应（ h（t）离散后 – h（n））

1
δ（t）的固定起始条件：	1、h(-1) = 0	2、h(0) = 1

卷积和（离散卷积）

1
方法：1、解析法	 2、图形法	 3、竖乘法性质：1、没有微积分

第七章 离散时间与系统 - 变换域

Z 变换的定义与收敛域，逆 Z 变换

定义：双边：X(z) = ∑ x(n) z^-n^ （ -∞ 到 ∞ ）

​ 单边：X(z) = ∑ x(n) z^-n^ （ 0 到 ∞ ）

收敛域ROC：

​ 达朗贝尔判别法；

​ n >= 0: |z| >= |a| ;

​ n < 0: |z| < |b| ;

逆z变换：

​ 右边序列：分母中高次项在左

​ 左边序列：分母中高次项在右

部分分式分解法：

​ X（z）写成零极点分式；

​ 写出 X（z）/ z 的分式并拆分；分母中（ z - a ）的 a 就可以写成 a^z^ ；

​ 右边序列：符号不变，u（ t ）

​ 左边序列：符号相反，- u（ - t ）

差分方程的 Z 变换求解

1
2
3
4
5
6
7
8
9
10
z变换的位移性质：		
L[x(n-m)u(n)] = z^(-m) * [X(z) + 从-m到-1对x(k)z^(-k)求和]		
由差分方程求 全 / 零输入 / 零状态 响应：

过程：	
1、两边取z变换	
2、提出 Y（z）并放到等式一边	
3、等式另一边分成两部分：		
第一部分没有X（z），是 零输入响应		
第二部分有 X（z），是 零状态响应

离散系统的系统函数 H（z）及频率响应

H（z）= Y（z）/ X（z）

通过系统函数 零极点 确定单位样值响应

对于因果序列：

​ 极点在单位圆内：稳定

​ 极点在单位圆内外：不稳定

左边序列刚好相反

最简离散框图

​ p354

稳定性与因果性

​ 因果性： 收敛域 |z| > |R|

​ 稳定性： H(z) 的收敛域包括单位圆

序列的傅里叶变换

p 366

F[ x ( n ) ] = X ( e^jw^ )

频率响应的几何作图法：

通过系统函数画出幅频特性、相频特性：
1、在图上画出零极点
2、w 从 单位圆上从（1,0）逆时针旋转
3、找到关键点（每个零极点的虚部）
4、代入关键点求值